Treasure Hunt
Treasure Hunt
http://poj.org/problem?id=1066
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 8233 | Accepted: 3402 |
Description
Archeologists from the Antiquities and Curios Museum (ACM) have flown to Egypt to examine the great pyramid of Key-Ops. Using state-of-the-art technology they are able to determine that the lower floor of the pyramid is constructed from a series of straightline walls, which intersect to form numerous enclosed chambers. Currently, no doors exist to allow access to any chamber. This state-of-the-art technology has also pinpointed the location of the treasure room. What these dedicated (and greedy) archeologists want to do is blast doors through the walls to get to the treasure room. However, to minimize the damage to the artwork in the intervening chambers (and stay under their government grant for dynamite) they want to blast through the minimum number of doors. For structural integrity purposes, doors should only be blasted at the midpoint of the wall of the room being entered. You are to write a program which determines this minimum number of doors.
An example is shown below:
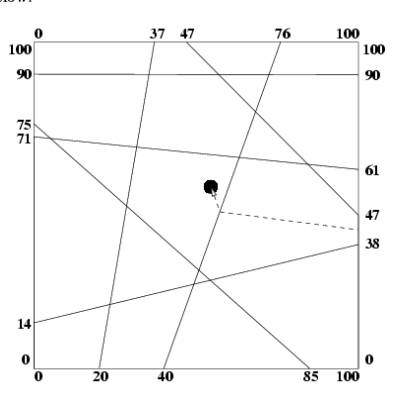
An example is shown below:

Input
The input will consist of one case. The first line will be an integer n (0 <= n <= 30) specifying number of interior walls, followed by n lines containing integer endpoints of each wall x1 y1 x2 y2 . The 4 enclosing walls of the pyramid have fixed endpoints at (0,0); (0,100); (100,100) and (100,0) and are not included in the list of walls. The interior walls always span from one exterior wall to another exterior wall and are arranged such that no more than two walls intersect at any point. You may assume that no two given walls coincide. After the listing of the interior walls there will be one final line containing the floating point coordinates of the treasure in the treasure room (guaranteed not to lie on a wall).
Output
Print a single line listing the minimum number of doors which need to be created, in the format shown below.
Sample Input
7 20 0 37 100 40 0 76 100 85 0 0 75 100 90 0 90 0 71 100 61 0 14 100 38 100 47 47 100 54.5 55.4
Sample Output
Number of doors = 2
Source
枚举边界上的点,要注意,枚举的步长为1会wa,步长要0.5= =

1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #include<cmath> 5 #include<vector> 6 #include<algorithm> 7 using namespace std; 8 const double eps=1e-8; 9 const double INF=1e20; 10 const double PI=acos(-1.0); 11 const int maxp=1010; 12 int sgn(double x){ 13 if(fabs(x)<eps) return 0; 14 if(x<0) return -1; 15 else return 1; 16 } 17 18 double hypot(double x,double y){ 19 return sqrt(x*x+y*y); 20 } 21 22 inline double sqr(double x){return x*x;} 23 struct Point{ 24 double x,y; 25 Point(){} 26 Point(double _x,double _y){ 27 x=_x; 28 y=_y; 29 } 30 void input(){ 31 scanf("%lf %lf",&x,&y); 32 } 33 void output(){ 34 printf("%.2f %.2f\n",x,y); 35 } 36 bool operator == (const Point &b)const{ 37 return sgn(x-b.x) == 0 && sgn(y-b.y)== 0; 38 } 39 bool operator < (const Point &b)const{ 40 return sgn(x-b.x)==0?sgn(y-b.y)<0:x<b.x; 41 } 42 Point operator - (const Point &b)const{ 43 return Point(x-b.x,y-b.y); 44 } 45 //叉积 46 double operator ^ (const Point &b)const{ 47 return x*b.y-y*b.x; 48 } 49 //点积 50 double operator * (const Point &b)const{ 51 return x*b.x+y*b.y; 52 } 53 //返回长度 54 double len(){ 55 return hypot(x,y); 56 } 57 //返回长度的平方 58 double len2(){ 59 return x*x+y*y; 60 } 61 //返回两点的距离 62 double distance(Point p){ 63 return hypot(x-p.x,y-p.y); 64 } 65 Point operator + (const Point &b)const{ 66 return Point(x+b.x,y+b.y); 67 } 68 Point operator * (const double &k)const{ 69 return Point(x*k,y*k); 70 } 71 Point operator / (const double &k)const{ 72 return Point(x/k,y/k); 73 } 74 75 //计算pa和pb的夹角 76 //就是求这个点看a,b所成的夹角 77 ///LightOJ1202 78 double rad(Point a,Point b){ 79 Point p=*this; 80 return fabs(atan2(fabs((a-p)^(b-p)),(a-p)*(b-p))); 81 } 82 //化为长度为r的向量 83 Point trunc(double r){ 84 double l=len(); 85 if(!sgn(l)) return *this; 86 r/=l; 87 return Point(x*r,y*r); 88 } 89 //逆时针转90度 90 Point rotleft(){ 91 return Point(-y,x); 92 } 93 //顺时针转90度 94 Point rotright(){ 95 return Point(y,-x); 96 } 97 //绕着p点逆时针旋转angle 98 Point rotate(Point p,double angle){ 99 Point v=(*this) -p; 100 double c=cos(angle),s=sin(angle); 101 return Point(p.x+v.x*c-v.y*s,p.y+v.x*s+v.y*c); 102 } 103 }; 104 105 struct Line{ 106 Point s,e; 107 Line(){} 108 Line(Point _s,Point _e){ 109 s=_s; 110 e=_e; 111 } 112 bool operator==(Line v){ 113 return (s==v.s)&&(e==v.e); 114 } 115 //根据一个点和倾斜角angle确定直线,0<=angle<pi 116 Line(Point p,double angle){ 117 s=p; 118 if(sgn(angle-PI/2)==0){ 119 e=(s+Point(0,1)); 120 } 121 else{ 122 e=(s+Point(1,tan(angle))); 123 } 124 } 125 //ax+by+c=0; 126 Line(double a,double b,double c){ 127 if(sgn(a)==0){ 128 s=Point(0,-c/b); 129 e=Point(1,-c/b); 130 } 131 else if(sgn(b)==0){ 132 s=Point(-c/a,0); 133 e=Point(-c/a,1); 134 } 135 else{ 136 s=Point(0,-c/b); 137 e=Point(1,(-c-a)/b); 138 } 139 } 140 void input(){ 141 s.input(); 142 e.input(); 143 } 144 void adjust(){ 145 if(e<s) swap(s,e); 146 } 147 //求线段长度 148 double length(){ 149 return s.distance(e); 150 } 151 //返回直线倾斜角 0<=angle<pi 152 double angle(){ 153 double k=atan2(e.y-s.y,e.x-s.x); 154 if(sgn(k)<0) k+=PI; 155 if(sgn(k-PI)==0) k-=PI; 156 return k; 157 } 158 //点和直线的关系 159 //1 在左侧 160 //2 在右侧 161 //3 在直线上 162 int relation(Point p){ 163 int c=sgn((p-s)^(e-s)); 164 if(c<0) return 1; 165 else if(c>0) return 2; 166 else return 3; 167 } 168 //点在线段上的判断 169 bool pointonseg(Point p){ 170 return sgn((p-s)^(e-s))==0&&sgn((p-s)*(p-e))<=0; 171 } 172 //两向量平行(对应直线平行或重合) 173 bool parallel(Line v){ 174 return sgn((e-s)^(v.e-v.s))==0; 175 } 176 //两线段相交判断 177 //2 规范相交 178 //1 非规范相交 179 //0 不相交 180 int segcrossseg(Line v){ 181 int d1=sgn((e-s)^(v.s-s)); 182 int d2=sgn((e-s)^(v.e-s)); 183 int d3=sgn((v.e-v.s)^(s-v.s)); 184 int d4=sgn((v.e-v.s)^(e-v.s)); 185 if((d1^d2)==-2&&(d3^d4)==-2) return 2; 186 return (d1==0&&sgn((v.s-s)*(v.s-e))<=0|| 187 d2==0&&sgn((v.e-s)*(v.e-e))<=0|| 188 d3==0&&sgn((s-v.s)*(s-v.e))<=0|| 189 d4==0&&sgn((e-v.s)*(e-v.e))<=0); 190 } 191 //直线和线段相交判断 192 //-*this line -v seg 193 //2 规范相交 194 //1 非规范相交 195 //0 不相交 196 int linecrossseg(Line v){ 197 int d1=sgn((e-s)^(v.s-s)); 198 int d2=sgn((e-s)^(v.e-s)); 199 if((d1^d2)==-2) return 2; 200 return (d1==0||d2==0); 201 } 202 //两直线关系 203 //0 平行 204 //1 重合 205 //2 相交 206 int linecrossline(Line v){ 207 if((*this).parallel(v)) 208 return v.relation(s)==3; 209 return 2; 210 } 211 //求两直线的交点 212 //要保证两直线不平行或重合 213 Point crosspoint(Line v){ 214 double a1=(v.e-v.s)^(s-v.s); 215 double a2=(v.e-v.s)^(e-v.s); 216 return Point((s.x*a2-e.x*a1)/(a2-a1),(s.y*a2-e.y*a1)/(a2-a1)); 217 } 218 //点到直线的距离 219 double dispointtoline(Point p){ 220 return fabs((p-s)^(e-s))/length(); 221 } 222 //点到线段的距离 223 double dispointtoseg(Point p){ 224 if(sgn((p-s)*(e-s))<0||sgn((p-e)*(s-e))<0) 225 return min(p.distance(s),p.distance(e)); 226 return dispointtoline(p); 227 } 228 //返回线段到线段的距离 229 //前提是两线段不相交,相交距离就是0了 230 double dissegtoseg(Line v){ 231 return min(min(dispointtoseg(v.s),dispointtoseg(v.e)),min(v.dispointtoseg(s),v.dispointtoseg(e))); 232 } 233 //返回点P在直线上的投影 234 Point lineprog(Point p){ 235 return s+(((e-s)*((e-s)*(p-s)))/((e-s).len2())); 236 } 237 //返回点P关于直线的对称点 238 Point symmetrypoint(Point p){ 239 Point q=lineprog(p); 240 return Point(2*q.x-p.x,2*q.y-p.y); 241 } 242 }; 243 244 Line L[1005]; 245 int n; 246 247 bool Check(Line a,Line b){ 248 if(sgn((a.s-a.e)^(b.s-a.e))*sgn((a.s-a.e)^(b.e-a.e))>0) return false; 249 if(sgn((b.s-b.e)^(a.s-b.e))*sgn((b.s-b.e)^(a.e-b.e))>0) return false; 250 if(sgn(max(a.s.x,a.e.x)-min(b.s.x,b.e.x))>=0&&sgn(max(b.s.x,b.e.x)-min(a.s.x,a.e.x))>=0 251 &&sgn(max(a.s.y,a.e.y)-min(b.s.y,b.e.y))>=0&&sgn(max(b.s.y,b.e.y)-min(a.s.y,a.e.y))>=0) 252 return true; 253 else return false; 254 } 255 256 257 double mp[115][115]; 258 259 int co; 260 261 int panduan(Line a){ 262 int sum=0; 263 for(int i=1;i<=n;i++){ 264 if(Check(a,L[i])){ 265 sum++; 266 } 267 } 268 return sum; 269 } 270 271 int main(){ 272 273 while(~scanf("%d",&n)){ 274 for(int i=1;i<=n;i++){ 275 scanf("%lf %lf %lf %lf",&L[i].s.x,&L[i].s.y,&L[i].e.x,&L[i].e.y); 276 } 277 int ans=0x3f3f3f3f; 278 Point goal; 279 scanf("%lf %lf",&goal.x,&goal.y); 280 Line tmp; 281 tmp.s=goal; 282 for(double i=0;i+eps<=100;i+=0.5){ 283 tmp.e.x=0,tmp.e.y=i; 284 ans=min(ans,panduan(tmp)); 285 tmp.e.x=i,tmp.e.y=0; 286 ans=min(ans,panduan(tmp)); 287 tmp.e.x=100,tmp.e.y=i; 288 ans=min(ans,panduan(tmp)); 289 tmp.e.x=i,tmp.e.y=100; 290 ans=min(ans,panduan(tmp)); 291 } 292 printf("Number of doors = %d\n",ans+1); 293 } 294 295 return 0; 296 }
posted on 2018-11-08 11:27 Fighting_sh 阅读(462) 评论(0) 编辑 收藏 举报




