Pick-up sticks
Pick-up sticks
http://poj.org/problem?id=2653
| Time Limit: 3000MS | Memory Limit: 65536K | |
| Total Submissions: 15265 | Accepted: 5752 |
Description
Stan has n sticks of various length. He throws them one at a time on the floor in a random way. After finishing throwing, Stan tries to find the top sticks, that is these sticks such that there is no stick on top of them. Stan has noticed that the last thrown stick is always on top but he wants to know all the sticks that are on top. Stan sticks are very, very thin such that their thickness can be neglected.
Input
Input consists of a number of cases. The data for each case start with 1 <= n <= 100000, the number of sticks for this case. The following n lines contain four numbers each, these numbers are the planar coordinates of the endpoints of one stick. The sticks are listed in the order in which Stan has thrown them. You may assume that there are no more than 1000 top sticks. The input is ended by the case with n=0. This case should not be processed.
Output
For each input case, print one line of output listing the top sticks in the format given in the sample. The top sticks should be listed in order in which they were thrown.
The picture to the right below illustrates the first case from input.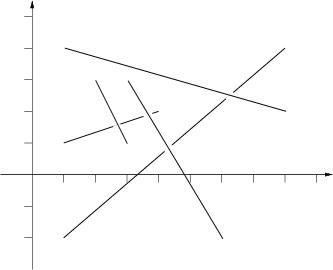
The picture to the right below illustrates the first case from input.

Sample Input
5 1 1 4 2 2 3 3 1 1 -2.0 8 4 1 4 8 2 3 3 6 -2.0 3 0 0 1 1 1 0 2 1 2 0 3 1 0
Sample Output
Top sticks: 2, 4, 5. Top sticks: 1, 2, 3.
Hint
Huge input,scanf is recommended.
这题判断是否相交就行
把bin巨的模板打了一遍。。。

1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #include<cmath> 5 using namespace std; 6 const double eps=1e-8; 7 const double INF=1e20; 8 const double PI=acos(-1.0); 9 const int maxp=1010; 10 int sgn(double x){ 11 if(fabs(x)<eps) return 0; 12 if(x<0) return -1; 13 else return 1; 14 } 15 inline double sqr(double x){return x*x;} 16 struct Point{ 17 double x,y; 18 Point(){} 19 Point(double _x,double _y){ 20 x=_x; 21 y=_y; 22 } 23 void input(){ 24 scanf("%lf %lf",&x,&y); 25 } 26 void output(){ 27 printf("%.2f %.2f\n",x,y); 28 } 29 bool operator == (const Point &b)const{ 30 return sgn(x-b.x) == 0 && sgn(y-b.y)== 0; 31 } 32 bool operator < (const Point &b)const{ 33 return sgn(x-b.x)==0?sgn(y-b.y)<0:x<b.x; 34 } 35 Point operator - (const Point &b)const{ 36 return Point(x-b.x,y-b.y); 37 } 38 //叉积 39 double operator ^ (const Point &b)const{ 40 return x*b.y-y*b.x; 41 } 42 //点积 43 double operator * (const Point &b)const{ 44 return x*b.x+y*b.y; 45 } 46 //返回长度 47 double len(){ 48 return hypot(x,y); 49 } 50 //返回长度的平方 51 double len2(){ 52 return x*x+y*y; 53 } 54 //返回两点的距离 55 double distance(Point p){ 56 return hypot(x-p.x,y-p.y); 57 } 58 Point operator + (const Point &b)const{ 59 return Point(x+b.x,y+b.y); 60 } 61 Point operator * (const double &k)const{ 62 return Point(x*k,y*k); 63 } 64 Point operator / (const double &k)const{ 65 return Point(x/k,y/k); 66 } 67 68 //计算pa和pb的夹角 69 //就是求这个点看a,b所成的夹角 70 ///LightOJ1202 71 double rad(Point a,Point b){ 72 Point p=*this; 73 return fabs(atan2(fabs((a-p)^(b-p)),(a-p)*(b-p))); 74 } 75 //化为长度为r的向量 76 Point trunc(double r){ 77 double l=len(); 78 if(!sgn(l)) return *this; 79 r/=l; 80 return Point(x*r,y*r); 81 } 82 //逆时针转90度 83 Point rotleft(){ 84 return Point(-y,x); 85 } 86 //顺时针转90度 87 Point rotright(){ 88 return Point(y,-x); 89 } 90 //绕着p点逆时针旋转angle 91 Point rotate(Point p,double angle){ 92 Point v=(*this) -p; 93 double c=cos(angle),s=sin(angle); 94 return Point(p.x+v.x*c-v.y*s,p.y+v.x*s+v.y*c); 95 } 96 }; 97 98 struct Line{ 99 Point s,e; 100 Line(){} 101 Line(Point _s,Point _e){ 102 s=_s; 103 e=_e; 104 } 105 bool operator==(Line v){ 106 return (s==v.s)&&(e==v.e); 107 } 108 //根据一个点和倾斜角angle确定直线,0<=angle<pi 109 Line(Point p,double angle){ 110 s=p; 111 if(sgn(angle-PI/2)==0){ 112 e=(s+Point(0,1)); 113 } 114 else{ 115 e=(s+Point(1,tan(angle))); 116 } 117 } 118 //ax+by+c=0; 119 Line(double a,double b,double c){ 120 if(sgn(a)==0){ 121 s=Point(0,-c/b); 122 e=Point(1,-c/b); 123 } 124 else if(sgn(b)==0){ 125 s=Point(-c/a,0); 126 e=Point(-c/a,1); 127 } 128 else{ 129 s=Point(0,-c/b); 130 e=Point(1,(-c-a)/b); 131 } 132 } 133 void input(){ 134 s.input(); 135 e.input(); 136 } 137 void adjust(){ 138 if(e<s) swap(s,e); 139 } 140 //求线段长度 141 double length(){ 142 return s.distance(e); 143 } 144 //返回直线倾斜角 0<=angle<pi 145 double angle(){ 146 double k=atan2(e.y-s.y,e.x-s.x); 147 if(sgn(k)<0) k+=PI; 148 if(sgn(k-PI)==0) k-=PI; 149 return k; 150 } 151 //点和直线的关系 152 //1 在左侧 153 //2 在右侧 154 //3 在直线上 155 int relation(Point p){ 156 int c=sgn((p-s)^(e-s)); 157 if(c<0) return 1; 158 else if(c>0) return 2; 159 else return 3; 160 } 161 //点在线段上的判断 162 bool pointonseg(Point p){ 163 return sgn((p-s)^(e-s))==0&&sgn((p-s)*(p-e))<=0; 164 } 165 //两向量平行(对应直线平行或重合) 166 bool parallel(Line v){ 167 return sgn((e-s)^(v.e-v.s))==0; 168 } 169 //两线段相交判断 170 //2 规范相交 171 //1 非规范相交 172 //0 不相交 173 int segcrossseg(Line v){ 174 int d1=sgn((e-s)^(v.s-s)); 175 int d2=sgn((e-s)^(v.e-s)); 176 int d3=sgn((v.e-v.s)^(s-v.s)); 177 int d4=sgn((v.e-v.s)^(e-v.s)); 178 if((d1^d2)==-2&&(d3^d4)==-2) return 2; 179 return (d1==0&&sgn((v.s-s)*(v.s-e))<=0|| 180 d2==0&&sgn((v.e-s)*(v.e-e))<=0|| 181 d3==0&&sgn((s-v.s)*(s-v.e))<=0|| 182 d4==0&&sgn((e-v.s)*(e-v.e))<=0); 183 } 184 //直线和线段相交判断 185 //-*this line -v seg 186 //2 规范相交 187 //1 非规范相交 188 //0 不相交 189 int linecrossseg(Line v){ 190 int d1=sgn((e-s)^(v.s-s)); 191 int d2=sgn((e-s)^(v.e-s)); 192 if((d1^d2)==-2) return 2; 193 return (d1==0||d2==0); 194 } 195 //两直线关系 196 //0 平行 197 //1 重合 198 //2 相交 199 int linecrossline(Line v){ 200 if((*this).parallel(v)) 201 return v.relation(s)==3; 202 return 2; 203 } 204 //求两直线的交点 205 //要保证两直线不平行或重合 206 Point crosspoint(Line v){ 207 double a1=(v.e-v.s)^(s-v.s); 208 double a2=(v.e-v.s)^(e-v.s); 209 return Point((s.x*a2-e.x*a1)/(a2-a1),(s.y*a2-e.y*a1)/(a2-a1)); 210 } 211 //点到直线的距离 212 double dispointtoline(Point p){ 213 return fabs((p-s)^(e-s))/length(); 214 } 215 //点到线段的距离 216 double dispointtoseg(Point p){ 217 if(sgn((p-s)*(e-s))<0||sgn((p-e)*(s-e))<0) 218 return min(p.distance(s),p.distance(e)); 219 return dispointtoline(p); 220 } 221 //返回线段到线段的距离 222 //前提是两线段不相交,相交距离就是0了 223 double dissegtoseg(Line v){ 224 return min(min(dispointtoseg(v.s),dispointtoseg(v.e)),min(v.dispointtoseg(s),v.dispointtoseg(e))); 225 } 226 //返回点P在直线上的投影 227 Point lineprog(Point p){ 228 return s+(((e-s)*((e-s)*(p-s)))/((e-s).len2())); 229 } 230 //返回点P关于直线的对称点 231 Point symmetrypoint(Point p){ 232 Point q=lineprog(p); 233 return Point(2*q.x-p.x,2*q.y-p.y); 234 } 235 }; 236 237 Line L[100005]; 238 int book[100005]; 239 int n; 240 241 bool Check(Line a,Line b){ 242 if(((a.s-a.e)^(b.s-a.e))*((a.s-a.e)^(b.e-a.e))>0) return false; 243 if(((b.s-b.e)^(a.s-b.e))*((b.s-b.e)^(a.e-b.e))>0) return false; 244 return true; 245 } 246 247 248 int main(){ 249 while(~scanf("%d",&n)){ 250 if(!n) break; 251 memset(book,0,sizeof(book)); 252 for(int i=1;i<=n;i++){ 253 scanf("%lf %lf %lf %lf",&L[i].s.x,&L[i].s.y,&L[i].e.x,&L[i].e.y); 254 } 255 int flag; 256 for(int i=1;i<=n;i++){ 257 flag=0; 258 for(int j=i+1;j<=n;j++){ 259 if(Check(L[i],L[j])){ 260 flag=1; 261 break; 262 } 263 } 264 if(flag){ 265 book[i]=1; 266 } 267 } 268 flag=0; 269 printf("Top sticks: "); 270 for(int i=1;i<=n;i++){ 271 if(!book[i]){ 272 if(!flag) flag=1; 273 else printf(", "); 274 printf("%d",i); 275 276 } 277 } 278 printf(".\n"); 279 } 280 return 0; 281 }
posted on 2018-11-06 21:52 Fighting_sh 阅读(337) 评论(0) 编辑 收藏 举报




