Feng Shui
Feng Shui
http://poj.org/problem?id=3384
| Time Limit: 2000MS | Memory Limit: 65536K | |||
| Total Submissions: 6627 | Accepted: 1972 | Special Judge | ||
Description
Feng shui is the ancient Chinese practice of placement and arrangement of space to achieve harmony with the environment. George has recently got interested in it, and now wants to apply it to his home and bring harmony to it.
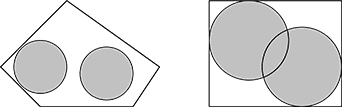
There is a practice which says that bare floor is bad for living area since spiritual energy drains through it, so George purchased two similar round-shaped carpets (feng shui says that straight lines and sharp corners must be avoided). Unfortunately, he is unable to cover the floor entirely since the room has shape of a convex polygon. But he still wants to minimize the uncovered area by selecting the best placing for his carpets, and asks you to help.
You need to place two carpets in the room so that the total area covered by both carpets is maximal possible. The carpets may overlap, but they may not be cut or folded (including cutting or folding along the floor border) — feng shui tells to avoid straight lines.
Input
The first line of the input file contains two integer numbers n and r — the number of corners in George’s room (3 ≤ n ≤ 100) and the radius of the carpets (1 ≤ r ≤ 1000, both carpets have the same radius). The following n lines contain two integers xi and yi each — coordinates of the i-th corner (−1000 ≤ xi, yi ≤ 1000). Coordinates of all corners are different, and adjacent walls of the room are not collinear. The corners are listed in clockwise order.
Output
Write four numbers x1, y1, x2, y2 to the output file, where (x1, y1) and (x2, y2) denote the spots where carpet centers should be placed. Coordinates must be precise up to 4 digits after the decimal point.
If there are multiple optimal placements available, return any of them. The input data guarantees that at least one solution exists.
Sample Input
| #1 | 5 2 -2 0 -5 3 0 8 7 3 5 0 |
|---|---|
| #2 | 4 3 0 0 0 8 10 8 10 0 |
Sample Output
| #1 | -2 3 3 2.5 |
|---|---|
| #2 | 3 5 7 3 |
Hint

1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 #include<vector> 5 #include<cmath> 6 #include<algorithm> 7 using namespace std; 8 const double eps=1e-8; 9 const double INF=1e20; 10 const double PI=acos(-1.0); 11 12 int sgn(double x){ 13 if(fabs(x)<eps) return 0; 14 if(x<0) return -1; 15 else return 1; 16 } 17 18 inline double sqr(double x){return x*x;} 19 inline double hypot(double a,double b){return sqrt(a*a+b*b);} 20 struct Point{ 21 double x,y; 22 Point(){} 23 Point(double _x,double _y){ 24 x=_x; 25 y=_y; 26 } 27 void input(){ 28 scanf("%lf %lf",&x,&y); 29 } 30 void output(){ 31 printf("%.2f %.2f\n",x,y); 32 } 33 bool operator == (const Point &b)const{ 34 return sgn(x-b.x) == 0 && sgn(y-b.y)== 0; 35 } 36 bool operator < (const Point &b)const{ 37 return sgn(x-b.x)==0?sgn(y-b.y)<0:x<b.x; 38 } 39 Point operator - (const Point &b)const{ 40 return Point(x-b.x,y-b.y); 41 } 42 //叉积 43 double operator ^ (const Point &b)const{ 44 return x*b.y-y*b.x; 45 } 46 //点积 47 double operator * (const Point &b)const{ 48 return x*b.x+y*b.y; 49 } 50 //返回长度 51 double len(){ 52 return hypot(x,y); 53 } 54 //返回长度的平方 55 double len2(){ 56 return x*x+y*y; 57 } 58 //返回两点的距离 59 double distance(Point p){ 60 return hypot(x-p.x,y-p.y); 61 } 62 Point operator + (const Point &b)const{ 63 return Point(x+b.x,y+b.y); 64 } 65 Point operator * (const double &k)const{ 66 return Point(x*k,y*k); 67 } 68 Point operator / (const double &k)const{ 69 return Point(x/k,y/k); 70 } 71 72 //计算pa和pb的夹角 73 //就是求这个点看a,b所成的夹角 74 ///LightOJ1202 75 double rad(Point a,Point b){ 76 Point p=*this; 77 return fabs(atan2(fabs((a-p)^(b-p)),(a-p)*(b-p))); 78 } 79 //化为长度为r的向量 80 Point trunc(double r){ 81 double l=len(); 82 if(!sgn(l)) return *this; 83 r/=l; 84 return Point(x*r,y*r); 85 } 86 //逆时针转90度 87 Point rotleft(){ 88 return Point(-y,x); 89 } 90 //顺时针转90度 91 Point rotright(){ 92 return Point(y,-x); 93 } 94 //绕着p点逆时针旋转angle 95 Point rotate(Point p,double angle){ 96 Point v=(*this) -p; 97 double c=cos(angle),s=sin(angle); 98 return Point(p.x+v.x*c-v.y*s,p.y+v.x*s+v.y*c); 99 } 100 }; 101 102 struct Line{ 103 Point s,e; 104 Line(){} 105 Line(Point _s,Point _e){ 106 s=_s; 107 e=_e; 108 } 109 bool operator==(Line v){ 110 return (s==v.s)&&(e==v.e); 111 } 112 //根据一个点和倾斜角angle确定直线,0<=angle<pi 113 Line(Point p,double angle){ 114 s=p; 115 if(sgn(angle-PI/2)==0){ 116 e=(s+Point(0,1)); 117 } 118 else{ 119 e=(s+Point(1,tan(angle))); 120 } 121 } 122 //ax+by+c=0; 123 Line(double a,double b,double c){ 124 if(sgn(a)==0){ 125 s=Point(0,-c/b); 126 e=Point(1,-c/b); 127 } 128 else if(sgn(b)==0){ 129 s=Point(-c/a,0); 130 e=Point(-c/a,1); 131 } 132 else{ 133 s=Point(0,-c/b); 134 e=Point(1,(-c-a)/b); 135 } 136 } 137 void input(){ 138 s.input(); 139 e.input(); 140 } 141 void adjust(){ 142 if(e<s) swap(s,e); 143 } 144 //求线段长度 145 double length(){ 146 return s.distance(e); 147 } 148 //返回直线倾斜角 0<=angle<pi 149 double angle(){ 150 double k=atan2(e.y-s.y,e.x-s.x); 151 if(sgn(k)<0) k+=PI; 152 if(sgn(k-PI)==0) k-=PI; 153 return k; 154 } 155 //点和直线的关系 156 //1 在左侧 157 //2 在右侧 158 //3 在直线上 159 int relation(Point p){ 160 int c=sgn((p-s)^(e-s)); 161 if(c<0) return 1; 162 else if(c>0) return 2; 163 else return 3; 164 } 165 //点在线段上的判断 166 bool pointonseg(Point p){ 167 return sgn((p-s)^(e-s))==0&&sgn((p-s)*(p-e))<=0; 168 } 169 //两向量平行(对应直线平行或重合) 170 bool parallel(Line v){ 171 return sgn((e-s)^(v.e-v.s))==0; 172 } 173 //两线段相交判断 174 //2 规范相交 175 //1 非规范相交 176 //0 不相交 177 int segcrossseg(Line v){ 178 int d1=sgn((e-s)^(v.s-s)); 179 int d2=sgn((e-s)^(v.e-s)); 180 int d3=sgn((v.e-v.s)^(s-v.s)); 181 int d4=sgn((v.e-v.s)^(e-v.s)); 182 if((d1^d2)==-2&&(d3^d4)==-2) return 2; 183 return (d1==0&&sgn((v.s-s)*(v.s-e))<=0|| 184 d2==0&&sgn((v.e-s)*(v.e-e))<=0|| 185 d3==0&&sgn((s-v.s)*(s-v.e))<=0|| 186 d4==0&&sgn((e-v.s)*(e-v.e))<=0); 187 } 188 //直线和线段相交判断 189 //-*this line -v seg 190 //2 规范相交 191 //1 非规范相交 192 //0 不相交 193 int linecrossseg(Line v){ 194 int d1=sgn((e-s)^(v.s-s)); 195 int d2=sgn((e-s)^(v.e-s)); 196 if((d1^d2)==-2) return 2; 197 return (d1==0||d2==0); 198 } 199 //两直线关系 200 //0 平行 201 //1 重合 202 //2 相交 203 int linecrossline(Line v){ 204 if((*this).parallel(v)) 205 return v.relation(s)==3; 206 return 2; 207 } 208 //求两直线的交点 209 //要保证两直线不平行或重合 210 Point crosspoint(Line v){ 211 double a1=(v.e-v.s)^(s-v.s); 212 double a2=(v.e-v.s)^(e-v.s); 213 return Point((s.x*a2-e.x*a1)/(a2-a1),(s.y*a2-e.y*a1)/(a2-a1)); 214 } 215 //点到直线的距离 216 double dispointtoline(Point p){ 217 return fabs((p-s)^(e-s))/length(); 218 } 219 //点到线段的距离 220 double dispointtoseg(Point p){ 221 if(sgn((p-s)*(e-s))<0||sgn((p-e)*(s-e))<0) 222 return min(p.distance(s),p.distance(e)); 223 return dispointtoline(p); 224 } 225 //返回线段到线段的距离 226 //前提是两线段不相交,相交距离就是0了 227 double dissegtoseg(Line v){ 228 return min(min(dispointtoseg(v.s),dispointtoseg(v.e)),min(v.dispointtoseg(s),v.dispointtoseg(e))); 229 } 230 //返回点P在直线上的投影 231 Point lineprog(Point p){ 232 return s+(((e-s)*((e-s)*(p-s)))/((e-s).len2())); 233 } 234 //返回点P关于直线的对称点 235 Point symmetrypoint(Point p){ 236 Point q=lineprog(p); 237 return Point(2*q.x-p.x,2*q.y-p.y); 238 } 239 }; 240 241 struct circle{ 242 Point p; 243 double r; 244 circle(){} 245 circle(Point _p,double _r){ 246 p=_p; 247 r=_r; 248 } 249 250 circle(double x,double y,double _r){ 251 p=Point(x,y); 252 r=_r; 253 } 254 255 circle(Point a,Point b,Point c){///三角形的外接圆 256 Line u=Line((a+b)/2,((a+b)/2)+((b-a).rotleft())); 257 Line v=Line((b+c)/2,((b+c)/2)+((c-b).rotleft())); 258 p=u.crosspoint(v); 259 r=p.distance(a); 260 } 261 262 circle(Point a,Point b,Point c,bool t){///三角形的内切圆 263 Line u,v; 264 double m=atan2(b.y-a.y,b.x-a.x),n=atan2(c.y-a.y,c.x-a.x); 265 u.s=a; 266 u.e=u.s+Point(cos((n+m)/2),sin((n+m)/2)); 267 v.s=b; 268 m=atan2(a.y-b.y,a.x-b.x),n=atan2(c.y-b.y,c.x-b.x); 269 v.e=v.s+Point(cos((n+m)/2),sin((n+m)/2)); 270 p=u.crosspoint(v); 271 r=Line(a,b).dispointtoseg(p); 272 } 273 274 void input(){ 275 p.input(); 276 scanf("%lf",&r); 277 } 278 279 void output(){ 280 printf("%.2f %.2f %.2f\n",p.x,p.y,r); 281 } 282 283 bool operator==(circle v){ 284 return (p==v.p)&&sgn(r-v.r)==0; 285 } 286 287 bool operator<(circle v)const{ 288 return ((p<v.p)||((p==v.p)&&sgn(r-v.r)<0)); 289 } 290 291 double area(){ 292 return PI*r*r; 293 } 294 295 double circumference(){ ///周长 296 return 2*PI*r; 297 } 298 299 int relation(Point b){///点和圆的关系 0圆外 1圆上 2圆内 300 double dst=b.distance(p); 301 if(sgn(dst-r)<0) return 2; 302 else if(sgn(dst-r)==0) return 1; 303 return 0; 304 } 305 306 int relationseg(Line v){///线段和圆的关系,比较的是圆心到线段的距离和半径的关系 307 double dst=v.dispointtoseg(p); 308 if(sgn(dst-r)<0) return 2; 309 else if(sgn(dst-r)==0) return 1; 310 return 0; 311 } 312 313 int relationline(Line v){///直线和圆的关系,比较的是圆心到直线的距离和半径的关系 314 double dst=v.dispointtoline(p); 315 if(sgn(dst-r)<0) return 2; 316 else if(sgn(dst-r)==0) return 1; 317 return 0; 318 } 319 320 int relationcircle(circle v){///两圆的关系 5相离 4外切 3相交 2内切 1内含 321 double d=p.distance(v.p); 322 if(sgn(d-r-v.r)>0) return 5; 323 if(sgn(d-r-v.r)==0) return 4; 324 double l=fabs(r-v.r); 325 if(sgn(d-r-v.r)<0&&sgn(d-l)>0) return 3; 326 if(sgn(d-l)==0) return 2; 327 if(sgn(d-l)<0) return 1; 328 } 329 330 int pointcrosscircle(circle v,Point &p1,Point &p2){///求两个圆的交点,0没有交点 1一个交点 2两个交点 331 int rel=relationcircle(v); 332 if(rel == 1 || rel == 5) return 0; 333 double d=p.distance(v.p); 334 double l=(d*d+r*r-v.r*v.r)/2*d; 335 double h=sqrt(r*r-l*l); 336 Point tmp=p+(v.p-p).trunc(l); 337 p1=tmp+((v.p-p).rotleft().trunc(h)); 338 p2=tmp+((v.p-p).rotright().trunc(h)); 339 if(rel == 2 || rel == 4) return 1; 340 return 2; 341 } 342 343 int pointcrossline(Line v,Point &p1,Point &p2){///求直线和圆的交点,返回交点的个数 344 if(!(*this).relationline(v)) return 0; 345 Point a=v.lineprog(p); 346 double d=v.dispointtoline(p); 347 d=sqrt(r*r-d*d); 348 if(sgn(d)==0) { 349 p1=a; 350 p2=a; 351 return 1; 352 } 353 p1=a+(v.e-v.s).trunc(d); 354 p2=a-(v.e-v.s).trunc(d); 355 return 2; 356 } 357 358 int getcircle(Point a,Point b,double r1,circle &c1,circle &c2){///得到过a,b两点,半径为r1的两个圆 359 circle x(a,r1),y(b,r1); 360 int t=x.pointcrosscircle(y,c1.p,c2.p); 361 if(!t) return 0; 362 c1.r=c2.r=r; 363 return t; 364 } 365 366 int getcircle(Line u,Point q,double r1,circle &c1,circle &c2){///得到与直线u相切,过点q,半径为r1的圆 367 double dis = u.dispointtoline(q); 368 if(sgn(dis-r1*2)>0) return 0; 369 if(sgn(dis)==0) { 370 c1.p=q+((u.e-u.s).rotleft().trunc(r1)); 371 c2.p=q+((u.e-u.s).rotright().trunc(r1)); 372 c1.r=c2.r=r1; 373 return 2; 374 } 375 Line u1=Line((u.s+(u.e-u.s).rotleft().trunc(r1)),(u.e+(u.e-u.s).rotleft().trunc(r1))); 376 Line u2=Line((u.s+(u.e-u.s).rotright().trunc(r1)),(u.e+(u.e-u.s).rotright().trunc(r1))); 377 circle cc=circle(q,r1); 378 Point p1,p2; 379 if(!cc.pointcrossline(u1,p1,p2)) cc.pointcrossline(u2,p1,p2); 380 c1=circle(p1,r1); 381 if(p1==p2){ 382 c2=c1; 383 return 1; 384 } 385 c2=circle(p2,r1); 386 return 2; 387 } 388 389 int getcircle(Line u,Line v,double r1,circle &c1,circle &c2,circle &c3,circle &c4){///同时与直线u,v相切,半径为r1的圆 390 if(u.parallel(v)) return 0;///两直线平行 391 Line u1=Line(u.s+(u.e-u.s).rotleft().trunc(r1),u.e+(u.e-u.s).rotleft().trunc(r1)); 392 Line u2=Line(u.s+(u.e-u.s).rotright().trunc(r1),u.e+(u.e-u.s).rotright().trunc(r1)); 393 Line v1=Line(v.s+(v.e-v.s).rotleft().trunc(r1),v.e+(v.e-v.s).rotleft().trunc(r1)); 394 Line v2=Line(v.s+(v.e-v.s).rotright().trunc(r1),v.e+(v.e-v.s).rotright().trunc(r1)); 395 c1.r=c2.r=c3.r=c4.r=r1; 396 c1.p=u1.crosspoint(v1); 397 c2.p=u1.crosspoint(v2); 398 c3.p=u2.crosspoint(v1); 399 c4.p=u2.crosspoint(v2); 400 return 4; 401 } 402 403 int getcircle(circle cx,circle cy,double r1,circle &c1,circle &c2){///同时与不相交圆 cx,cy相切,半径为r1的圆 404 circle x(cx.p,r1+cx.r),y(cy.p,r1+cy.r); 405 int t=x.pointcrosscircle(y,c1.p,c2.p); 406 if(!t) return 0; 407 c1.r=c2.r=r1; 408 return t; 409 } 410 411 int tangentline(Point q,Line &u,Line &v){///过一点作圆的切线(先判断点和圆的关系) 412 int x=relation(q); 413 if(x==2) return 0; 414 if(x==1){ 415 u=Line(q,q+(q-p).rotleft()); 416 v=u; 417 return 1; 418 } 419 double d=p.distance(q); 420 double l=r*r/d; 421 double h=sqrt(r*r-l*l); 422 u=Line(q,p+((q-p).trunc(l)+(q-p).rotleft().trunc(h))); 423 v=Line(q,p+((q-p).trunc(l)+(q-p).rotright().trunc(h))); 424 return 2; 425 } 426 427 double areacircle(circle v){///求两圆相交的面积 428 int rel=relationcircle(v); 429 if(rel >= 4) return 0.0; 430 if(rel <= 2) return min(area(),v.area()); 431 double d=p.distance(v.p); 432 double hf=(r+v.r+d)/2.0; 433 double ss=2*sqrt(hf*(hf-r)*(hf-v.r)*(hf-d)); 434 double a1=acos((r*r+d*d-v.r*v.r)/(2.0*r*d)); 435 a1=a1*r*r; 436 double a2=acos((v.r*v.r+d*d-r*r)/(2.0*v.r*d)); 437 a2=a2*v.r*v.r; 438 return a1+a2-ss; 439 } 440 441 double areatriangle(Point a,Point b){///求圆和三角形pab的相交面积 442 if(sgn((p-a)^(p-b))==0) return 0.0; 443 Point q[5]; 444 int len=0; 445 q[len++]=a; 446 Line l(a,b); 447 Point p1,p2; 448 if(pointcrossline(l,q[1],q[2])==2){ 449 if(sgn((a-q[1])*(b-q[1]))<0) q[len++]=q[1]; 450 if(sgn((a-q[2])*(b-q[2]))<0) q[len++]=q[2]; 451 } 452 q[len++]=b; 453 if(len==4 && sgn((q[0]-q[1])*(q[2]-q[1]))>0) swap(q[1],q[2]); 454 double res=0; 455 for(int i=0;i<len-1;i++){ 456 if(relation(q[i])==0||relation(q[i+1])==0){ 457 double arg=p.rad(q[i],q[i+1]); 458 res+=r*r*arg/2.0; 459 } 460 else{ 461 res+=fabs((q[i]-p)^(q[i+1]-p))/2.0; 462 } 463 } 464 return res; 465 } 466 }; 467 468 struct polygon{ 469 int n; 470 Point p[100010]; 471 Line l[100010]; 472 void input(int _n){ 473 n=_n; 474 for(int i=0;i<n;i++){ 475 p[i].input(); 476 } 477 } 478 479 void add(Point q){ 480 p[n++]=q; 481 } 482 483 void getline(){ 484 for(int i=0;i<n;i++){ 485 l[i]=Line(p[i],p[(i+1)%n]); 486 } 487 } 488 489 struct cmp{ 490 Point p; 491 cmp(const Point &p0){p=p0;} 492 bool operator()(const Point &aa,const Point &bb){ 493 Point a=aa,b=bb; 494 int d=sgn((a-p)^(b-p)); 495 if(d==0){ 496 return sgn(a.distance(p)-b.distance(p))<0; 497 } 498 return d>0; 499 } 500 }; 501 502 void norm(){///进行极角排序 503 Point mi=p[0]; 504 for(int i=1;i<n;i++){ 505 mi=min(mi,p[i]); 506 } 507 sort(p,p+n,cmp(mi)); 508 } 509 510 void getconvex(polygon &convex){///得到第一种凸包的方法,编号为0~n-1,可能要特判所有点共点或共线的特殊情况 511 sort(p,p+n); 512 convex.n=n; 513 for(int i=0;i<min(n,2);i++){ 514 convex.p[i]=p[i]; 515 } 516 if(convex.n==2&&(convex.p[0]==convex.p[1])) convex.n--; 517 if(n<=2) return; 518 int &top=convex.n; 519 top=1; 520 for(int i=2;i<n;i++){ 521 while(top&&sgn((convex.p[top]-p[i])^(convex.p[top-1]-p[i]))<0) top--; 522 convex.p[++top]=p[i]; 523 } 524 int temp=top; 525 convex.p[++top]=p[n-2]; 526 for(int i=n-3;i>=0;i--){ 527 while(top!=temp&&sgn((convex.p[top]-p[i])^(convex.p[top-1]-p[i]))<=0) top--; 528 convex.p[++top]=p[i]; 529 } 530 if(convex.n==2&&(convex.p[0]==convex.p[1])) convex.n--; 531 convex.norm(); 532 } 533 534 void Graham(polygon &convex){///得到凸包的第二种方法 535 norm(); 536 int &top=convex.n; 537 top=0; 538 if(n==1){ 539 top=1; 540 convex.p[0]=p[0]; 541 return; 542 } 543 if(n==2){ 544 top=2; 545 convex.p[0]=p[0]; 546 convex.p[1]=p[1]; 547 if(convex.p[0]==convex.p[1]) top--; 548 return; 549 } 550 convex.p[0]=p[0]; 551 convex.p[1]=p[1]; 552 top=2; 553 for(int i=2;i<n;i++){ 554 while(top>1&&sgn((convex.p[top-1]-convex.p[top-2])^(p[i]-convex.p[top-2]))<=0) top--; 555 convex.p[top++]=p[i]; 556 } 557 if(convex.n==2 && (convex.p[0]==convex.p[1])) convex.n--; 558 } 559 560 bool inconvex(){///判断是不是凸的 561 bool s[3]; 562 memset(s,false,sizeof(s)); 563 for(int i=0;i<n;i++){ 564 int j=(i+1)%n; 565 int k=(j+1)%n; 566 s[sgn((p[j]-p[i])^(p[k]-p[i]))+1]=true; 567 if(s[0]&&s[2]) return false; 568 } 569 return true; 570 } 571 572 int relationpoint(Point q){///判断点和任意多边形的关系 3点上 2边上 1内部 0外部 573 for(int i=0;i<n;i++){ 574 if(p[i]==q) return 3; 575 } 576 getline(); 577 for(int i=0;i<n;i++){ 578 if(l[i].pointonseg(q)) return 2; 579 } 580 int cnt=0; 581 for(int i=0;i<n;i++){ 582 int j=(i+1)%n; 583 int k=sgn((q-p[j])^(p[i]-p[j])); 584 int u=sgn(p[i].y-q.y); 585 int v=sgn(p[j].y-q.y); 586 if(k>0&&u<0&&v>=0) cnt++; 587 if(k<0&&v<0&&u>=0) cnt--; 588 } 589 return cnt!=0; 590 } 591 592 void convexcnt(Line u,polygon &po){///直线u切割凸多边形左侧 注意直线方向 593 int &top=po.n; 594 top=0; 595 for(int i=0;i<n;i++){ 596 int d1=sgn((u.e-u.s)^(p[i]-u.s)); 597 int d2=sgn((u.e-u.s)^(p[(i+1)%n]-u.s)); 598 if(d1>=0) po.p[top++]=p[i]; 599 if(d1*d2<0)po.p[top++]=u.crosspoint(Line(p[i],p[(i+1)%n])); 600 } 601 } 602 603 double getcircumference(){///得到周长 604 double sum=0; 605 for(int i=0;i<n;i++){ 606 sum+=p[i].distance(p[(i+1)%n]); 607 } 608 return sum; 609 } 610 611 double getarea(){///得到面积 612 double sum=0; 613 for(int i=0;i<n;i++){ 614 sum+=(p[i]^p[(i+1)%n]); 615 } 616 return fabs(sum)/2; 617 } 618 619 bool getdir(){///得到方向 1表示逆时针 0表示顺时针 620 double sum=0; 621 for(int i=0;i<n;i++){ 622 sum+=(p[i]^p[(i+1)%n]); 623 } 624 if(sgn(sum)>0) return 1; 625 return 0; 626 } 627 628 Point getbarycentre(){///得到重心 629 Point ret(0,0); 630 double area=0; 631 for(int i=1;i<n-1;i++){ 632 double tmp=(p[i]-p[0])^(p[i+1]-p[0]); 633 if(sgn(tmp)==0) continue; 634 area+=tmp; 635 ret.x+=(p[0].x+p[i].x+p[i+1].x)/3*tmp; 636 ret.y+=(p[0].y+p[i].y+p[i+1].y)/3*tmp; 637 } 638 if(sgn(area)) ret =ret/area; 639 return ret; 640 } 641 642 double areacircle(circle c){///多边形和圆交的面积 643 double ans=0; 644 for(int i=0;i<n;i++){ 645 int j=(i+1)%n; 646 if(sgn((p[j]-c.p)^(p[i]-c.p))>=0) ans+=c.areatriangle(p[i],p[j]); 647 else ans-=c.areatriangle(p[i],p[j]); 648 } 649 return fabs(ans); 650 } 651 652 int relationcircle(circle c){///多边形和圆的关系 2圆完全在多边形内 1圆在多边形里面,碰到了多边形的边界 0其他 653 getline(); 654 int x=2; 655 if(relationpoint(c.p)!=1) return 0; 656 for(int i=0;i<n;i++){ 657 if(c.relationseg(l[i])==2) return 0; 658 if(c.relationseg(l[i])==1) x=1; 659 } 660 return x; 661 } 662 }; 663 664 struct halfplane:public Line{ 665 double angle; 666 halfplane(){} 667 halfplane(Point _s,Point _e){///表示向量s->e逆时针(左侧)的半平面 668 s=_s; 669 e=_e; 670 } 671 halfplane(Line v){ 672 s=v.s; 673 e=v.e; 674 } 675 void calcangle(){ 676 angle=atan2(e.y-s.y,e.x-s.x); 677 } 678 bool operator<(const halfplane &b)const{ 679 return angle<b.angle; 680 } 681 }; 682 683 struct halfplanes{ 684 int n; 685 halfplane hp[2020]; 686 Point p[2020]; 687 int que[2020]; 688 int st,ed; 689 void push(halfplane tmp){ 690 hp[n++]=tmp; 691 } 692 693 void unique(){///去重 694 int m=1; 695 for(int i=1;i<n;i++){ 696 if(sgn(hp[i].angle-hp[i-1].angle)!=0) hp[m++]=hp[i]; 697 else if(sgn((hp[m-1].e-hp[m-1].s)^(hp[i].s-hp[m-1].s))>0) hp[m-1]=hp[i]; 698 } 699 n=m; 700 } 701 bool halfplaneinsert(){ 702 for(int i=0;i<n;i++) hp[i].calcangle(); 703 sort(hp,hp+n); 704 unique(); 705 que[st=0]=0; 706 que[ed=1]=1; 707 p[1]=hp[0].crosspoint(hp[1]); 708 for(int i=2;i<n;i++){ 709 while(st<ed&&sgn((hp[i].e-hp[i].s)^(p[ed]-hp[i].s))<0) ed--; 710 while(st<ed&&sgn((hp[i].e-hp[i].s)^(p[st+1]-hp[i].s))<0) st++; 711 que[++ed]=i; 712 if(hp[i].parallel(hp[que[ed-1]])) return false; 713 p[ed]=hp[i].crosspoint(hp[que[ed-1]]); 714 } 715 while(st<ed&&sgn((hp[que[st]].e-hp[que[st]].s)^(p[ed]-hp[que[st]].s))<0) ed--; 716 while(st<ed&&sgn((hp[que[ed]].e-hp[que[ed]].s)^(p[st+1]-hp[que[ed]].s))<0) st++; 717 if(st+1>=ed) return false; 718 return true; 719 } 720 721 void getconvex(polygon &con){///得到最后半平面交得到的凸多边形,要先调用halfplaneinsert()且返回true 722 p[st]=hp[que[st]].crosspoint(hp[que[ed]]); 723 con.n=ed-st+1; 724 for(int j=st,i=0;j<=ed;i++,j++){ 725 con.p[i]=p[j]; 726 } 727 } 728 }; 729 730 bool Check(Line a,Line b){ 731 if(sgn((a.s-a.e)^(b.s-a.e))*sgn((a.s-a.e)^(b.e-a.e))>0) return false; 732 if(sgn((b.s-b.e)^(a.s-b.e))*sgn((b.s-b.e)^(a.e-b.e))>0) return false; 733 if(sgn(max(a.s.x,a.e.x)-min(b.s.x,b.e.x))>=0&&sgn(max(b.s.x,b.e.x)-min(a.s.x,a.e.x))>=0 734 &&sgn(max(a.s.y,a.e.y)-min(b.s.y,b.e.y))>=0&&sgn(max(b.s.y,b.e.y)-min(a.s.y,a.e.y))>=0) 735 return true; 736 else return false; 737 } 738 739 halfplanes hps; 740 halfplane hp; 741 int n; 742 Point p[105]; 743 polygon poly; 744 745 746 void change(Point a,Point b,Point &c,Point &d,double p)///将线段ab往左移动距离p 747 { 748 double len = a.distance(b); 749 double dx = (a.y - b.y)*p/len; 750 double dy = (b.x - a.x)*p/len; 751 c.x = a.x + dx; c.y = a.y + dy; 752 d.x = b.x + dx; d.y = b.y + dy; 753 } 754 755 int main(){ 756 int n; 757 double r; 758 while(~scanf("%d %lf",&n,&r)){ 759 for(int i=0;i<n;i++){ 760 p[i].input(); 761 } 762 hps.n=0; 763 Point aa,bb; 764 for(int i=0;i<n;i++){ 765 change(p[(i+1)%n],p[i],aa,bb,r); 766 hps.push(halfplane(aa,bb)); 767 } 768 hps.halfplaneinsert(); 769 hps.getconvex(poly); 770 int ans1=0,ans2=0; 771 for(int i=0;i<poly.n;i++){ 772 for(int j=i;j<poly.n;j++){ 773 if(sgn(poly.p[i].distance(poly.p[j])-poly.p[ans1].distance(poly.p[ans2]))>0){ 774 ans1=i,ans2=j; 775 } 776 } 777 } 778 printf("%.4f %.4f %.4f %.4f\n",poly.p[ans1].x,poly.p[ans1].y,poly.p[ans2].x,poly.p[ans2].y); 779 } 780 return 0; 781 }
posted on 2019-05-05 21:56 Fighting_sh 阅读(477) 评论(0) 编辑 收藏 举报




