Honeycomb

Honeycomb

http://codeforces.com/gym/102028/problem/F

time limit per test
4.0 s
memory limit per test
1024 MB
input
standard input
output
standard output

A honeycomb is a mass wax cells built by honey bees, which can be described as a regular tiling of the Euclidean plane, in which three hexagons meet at each internal vertex. The internal angle of a hexagon is 120120 degrees, so three hexagons at a point make a full 360360degrees. The following figure shows a complete honeycomb with 33 rows and 44 columns.

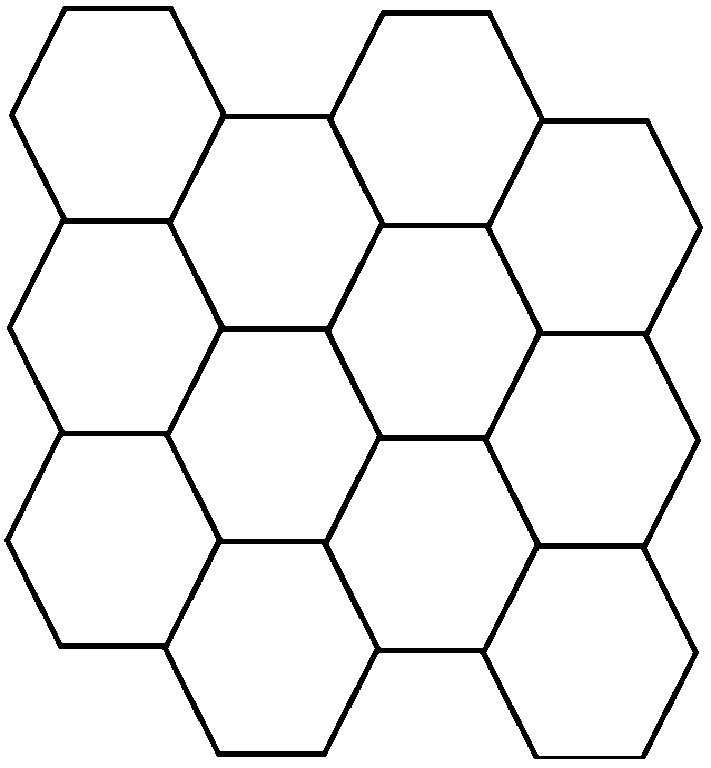
Here we guarantee that the first cell in the second column always locates in the bottom right side of the first cell in the first column, as shown above. A general honeycomb may, on the basis of a complete honeycomb, lose some walls between adjacent cells, but the honeycomb is still in a closed form. A possible case looks like the figure below.

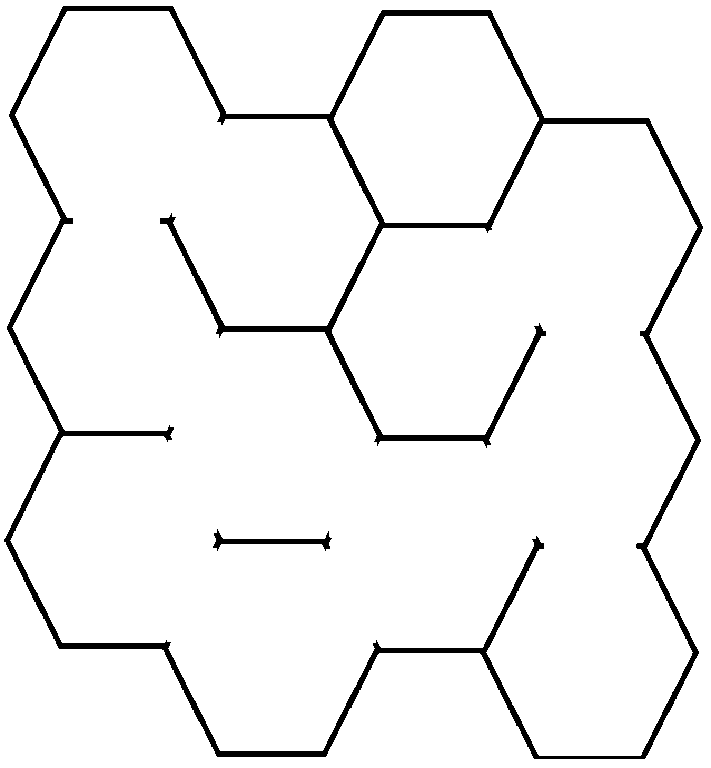
Hamilton is a brave bee living in a general honeycomb. Now he wants to move from a starting point to a specified destination. The image below gives a feasible path in a 3×43×4 honeycomb from the 11-st cell in the 22-nd column to the 11-st cell in the 44-th column.

Please help him find the minimum number of cells that a feasible path has to pass through (including the starting point and the destination) from the specified starting point to the destination.

Input

The input contains several test cases, and the first line contains a positive integer TT indicating the number of test cases which is up to 104104.

For each test case, the first line contains two integers rr and cc indicating the number of rows and the number of columns of the honeycomb, where 2≤r,c≤1032≤r,c≤103.

The following (4r+3)(4r+3) lines describe the whole given honeycomb, where each line contains at most (6c+3)(6c+3) characters. Odd lines contain grid vertices represented as plus signs ("+") and zero or more horizontal edges, while even lines contain two or more diagonal edges. Specifically, a cell is described as 66 vertices and at most 66 edges. Its upper boundary or lower boundary is represented as three consecutive minus signs ("-"). Each one of its diagonal edges, if exists, is a single forward slash ("/") or a single backslash ("\") character. All edge characters will be placed exactly between the corresponding vertices. At the center of the starting cell (resp. the destination), a capital "S" (resp. a capital "T") as a special character is used to indicate the special cell. All other characters will be space characters. Note that if any input line could contain trailing whitespace, that whitespace will be omitted.

We guarantee that all outermost wall exist so that the given honeycomb is closed, and exactly one "S" and one "T" appear in the given honeycomb. Besides, the sum of r⋅cr⋅c in all test cases is up to 2×1062×106.

Output

For each test case, output a line containing the minimum number of cells that Hamilton has to visit moving from the starting cell ("S") to the destination ("T"), including the starting cell and the destination. If no feasible path exists, output -1 instead.

Example
input
Copy
1
3 4
  +---+       +---+
 /     \     /     \
+       +---+       +---+
 \           \     /     \
  +   +   S   +---+   T   +
 /     \     /           /
+       +---+       +   +
 \           \     /     \
  +---+       +---+       +
 /                       /
+       +---+       +   +
 \                 /     \
  +---+       +---+       +
       \     /     \     /
        +---+       +---+
output
Copy
7

 

比赛的时候煞笔了，没写出来。。。

  1 #include<iostream>
  2 #include<cstring>
  3 #include<string>
  4 #include<algorithm>
  5 #include<cmath>
  6 #include<queue>
  7 #include<stack>
  8 #include<cstdio>
  9 #include<vector>
 10 using namespace std;
 11 
 12 int n,m,fanwei;
 13 struct sair{
 14     int pos,step;
 15 };
 16 
 17 char str[4105][6105];
 18 int book[2000005];
 19 vector<int> ve[2000005];
 20 
 21 void bfs(int ss,int tt){
 22     sair s,e;
 23     queue<sair>Q;
 24     s.pos=ss,s.step=1;
 25     book[ss]=1;
 26     Q.push(s);
 27     while(!Q.empty()){
 28         s=Q.front();
 29         Q.pop();
 30         for(int i=0;i<ve[s.pos].size();i++){
 31             if(ve[s.pos][i]>=1&&ve[s.pos][i]<=fanwei&&!book[ve[s.pos][i]]){
 32                 book[ve[s.pos][i]]=1;
 33                 e.pos=ve[s.pos][i];
 34                 e.step=s.step+1;
 35                 if(e.pos==tt){
 36                     printf("%d\n",e.step);
 37                     return;
 38                 }
 39                 Q.push(e);
 40             }
 41         }
 42     }
 43     printf("-1\n");
 44 }
 45 
 46 void join(int x,int y){
 47     ve[x].push_back(y);
 48     ve[y].push_back(x);
 49     ////如果wa的话，加单向边试试？？
 50 }
 51 
 52 int main(){
 53     int T;
 54     scanf("%d",&T);
 55     while(T--){
 56         scanf("%d %d%*c",&n,&m);
 57         int tmp=n*m;
 58         fanwei=tmp;
 59         for(int i=0;i<=tmp;i++){
 60             book[i]=0;
 61             ve[i].clear();
 62         }
 63         for(int i=0;i<n*4+3;i++){
 64            gets(str[i]);
 65         }
 66 
 67         //最后三行不用判断
 68         int nn=n*4;
 69         int co;
 70         for(int i=0;i<nn;i++){
 71             int len=strlen(str[i]);
 72             int j=0;
 73             if(i%4==0){
 74                 j=4;
 75                 co=1;
 76                 while(j<len){
 77                     if(str[i][j]==' '){
 78                         join((i/4-1)*m+co,i/4*m+co);
 79                         
 80                     }
 81                     co+=2;
 82                     j+=12;
 83                 }
 84             }
 85             else if(i%4==1){
 86                 j=1;
 87                 co=1;
 88                 while(j<len){
 89                     if(str[i][j]==' '){
 90                         join((i/4-1)*m+co-1,i/4*m+co);
 91                     }
 92                     j+=12;
 93                     co+=2;
 94                 }
 95                 j=7;
 96                 co=1;
 97                 while(j<len){
 98                     if(str[i][j]==' '){
 99                         join((i/4-1)*m+co+1,i/4*m+co);
100                     }
101                     j+=12;
102                     co+=2;
103                 }
104             }
105             else if(i%4==2){
106                 co=2;
107                 j=10;
108                 while(j<len){
109                     if(str[i][j]==' '){
110                         join((i/4-1)*m+co,i/4*m+co);           
111                     }
112                     co+=2;
113                     j+=12;
114                 }
115                 
116             }
117             else if(i%4==3){
118                 j=1;
119                 co=1;
120                 while(j<len){
121                     if(str[i][j]==' '){
122                         join(i/4*m+co,i/4*m+co-1);
123                     }
124                     j+=12;
125                     co+=2;
126                 }
127                 j=7;
128                 co=2;
129                 while(j<len){
130                     if(str[i][j]==' '){
131                         join(i/4*m+co,i/4*m+co-1);
132 
133                     }
134                     j+=12;
135                     co+=2;
136                 }
137             }
138         }
139         int s=-1,t=-1;
140         nn=n*4;
141         int xxx=0;
142         for(int i=2;i<nn;i+=4){
143             int len=strlen(str[i]);
144             int j=4;
145             co=xxx*m+1;
146             xxx++;
147             while(j<len){
148                 if(str[i][j]=='S'){
149                     s=co;
150                 }
151                 else if(str[i][j]=='T'){
152                     t=co;
153                 }
154                 j+=12;
155                 co+=2;
156             }
157         }
158         nn+=2;
159         xxx=0;
160         for(int i=4;i<nn;i+=4){
161             int len=strlen(str[i]);
162             int j=10;
163             co=xxx*m+2;
164             xxx++;
165             while(j<len){
166                 if(str[i][j]=='S'){
167                     s=co;
168                 }
169                 else if(str[i][j]=='T'){
170                     t=co;
171                 }
172                 j+=12;
173                 co+=2;
174             }
175         }
176         //cout<<s<<" "<<t<<endl;
177         bfs(s,t);
178     }
179 
180    // system("pause");
181 
182     return 0;
183 }
184 /*
185 100
186 3 4
187   +---+       +---+
188  /     \     /     \
189 +       +---+       +---+
190  \           \     /     \
191   +   +   S   +---+   T   +
192  /     \     /           /
193 +       +---+       +   +
194  \           \     /     \
195   +---+       +---+       +
196  /                       /
197 +       +---+       +   +
198  \                 /     \
199   +---+       +---+       +
200        \     /     \     /
201         +---+       +---+
202 
203 3 4
204   +---+       +---+
205  /     \     /     \
206 +       +---+       +---+
207  \           \     /     \
208   +   +   S   +---+       +
209  /     \     /           /
210 +       +---+       +   +
211  \           \     /     \
212   +---+   T   +---+       +
213  /           /           /
214 +       +---+       +   +
215  \                 /     \
216   +---+       +---+       +
217        \     /     \     /
218         +---+       +---+
219 
220 3 3
221   +---+       +---+
222  /     \     /     \
223 +       +---+       +
224  \           \     /   
225   +   +   S   +---+   
226  /     \     /     \    
227 +       +---+       +
228  \           \     / 
229   +---+   T   +---+      
230  /           /     \  
231 +       +---+       + 
232  \                 /    
233   +---+       +---+     
234        \     /    
235         +---+    
236 */
View Code

 

posted on 2018-12-08 17:55  Fighting_sh  阅读(462)  评论(0)  编辑  收藏  举报

导航