C++ Primier Plus(第六版) 第十一章 使用类 编程练习答案
1. 修改程序清单11.5,使之将一系列连续的随机漫步者位置写入到文件中。对于每个位置,用步号进行标示。另外,让该程序将初始条件(目标距离和步长)以及结果小结写入到该文件中。该文件的内容与下面类似:
Target Distance: 100, Step Size: 20
0: (x,y) = (0,0)
1: (x,y) = (-11.4715, 16.383)
2: (x,y) = (-8.68807, -3.42232)
...
26: (x,y) = (42.2919, -78.2594)
27: (x,y) = (58.6794, -89.7309)
After 27 steps, the subject has the following location:
(x,y) = (58.6749, -89.7309)
or
(m,a) = (107.212, -56.8194)
本题比较容易,重新帮助熟练程序写入文件。vector.h和vector.cpp本章里都有,主函数的程序如下:
// ex1.cpp -- walk random problem
// compile with vector.cpp
#include <fstream>
#include <cstdlib> // rand(), srand() protypes
#include <ctime> // time() protype
#include "vector.h"
int main()
{
using namespace std;
using VECTOR::Vector;
// write in file
ofstream fout;
fout.open("walk_random.txt");
srand(time(0)); //generate a seed of random
double target;
double dstep;
unsigned long steps = 0;
Vector step;
Vector result(0.0,0.0);
cout << "Enter the Target Distance(enter q to quit): ";
while(cin >> target)
{
cout << "Enter the distance of every step: ";
while(!(cin >> dstep))
{
cin.clear();
while(cin.get() != '\n')
continue;
cout << "Bad input, please enter a double value: ";
}
fout << "Target Distance: " << target << ", Step Size: " << dstep << endl;
while(result.mag_val() < target)
{
step.reset(dstep, rand() % 360, Vector::POL);
step.rect_mode();
fout << steps << ": " << step << endl;
result = result + step;
steps++;
}
fout << "After " << steps << " steps, the subject has the following location:\n";
fout << result << endl;
fout << "or\n";
result.polar_mode();
fout << result << endl;
fout << "Average outward distance per step = " << result.mag_val() / steps << endl;
cout << "Enter next Target Distance(enter q to quit): ";
}
fout.close();
cout << "Bye\n";
return 0;
}
运行结果如下:
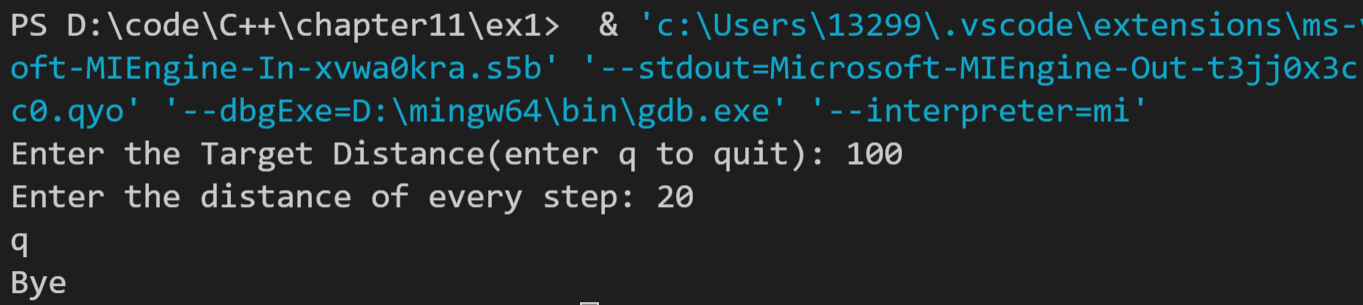
生成的文件如下:
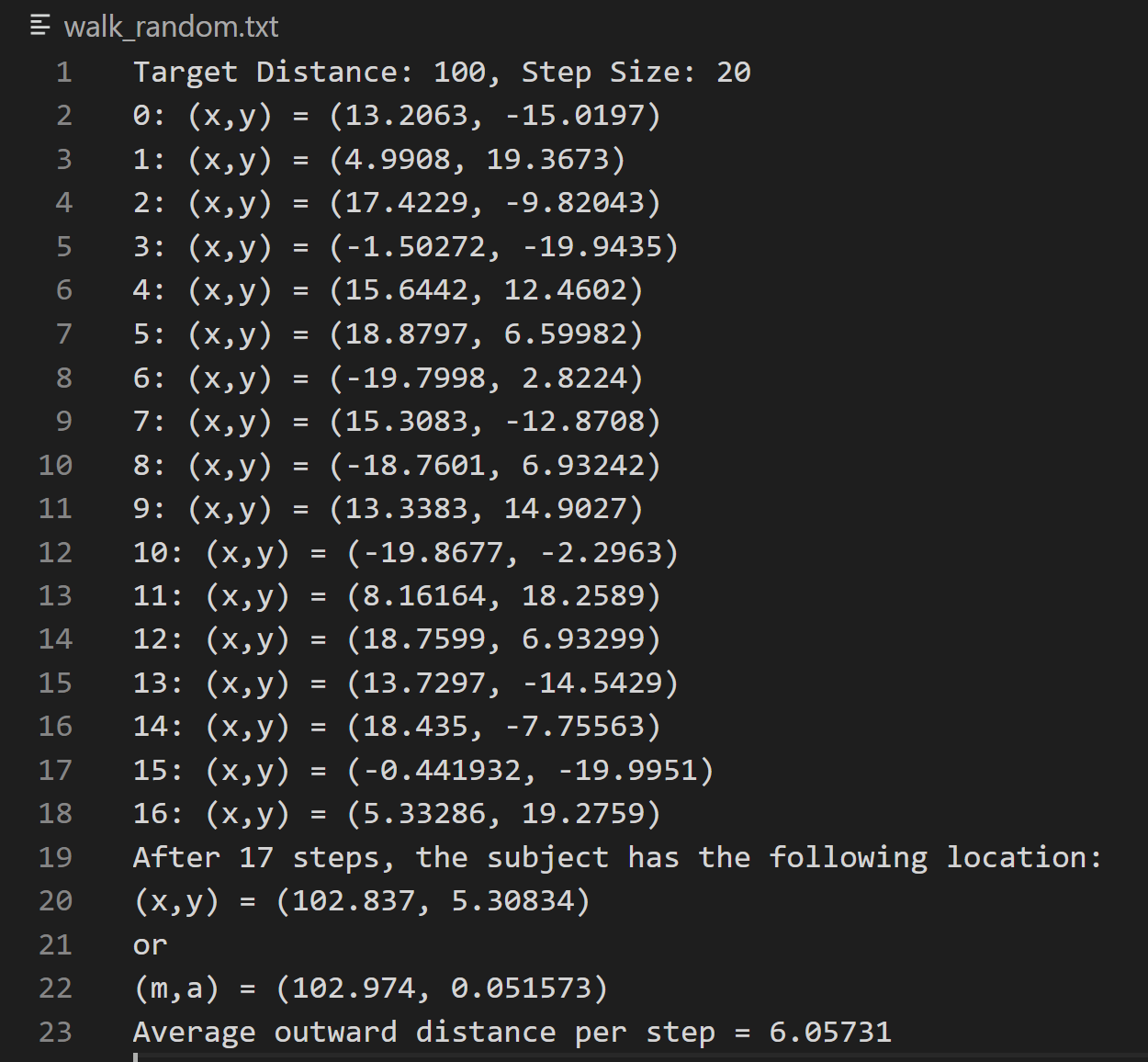
2. 对Vector类的头文件(程序清单11.13)和实现文件(程序清单11.14进行修改),使其不再存储矢量的长度和角度,而是在magval()和angvel()被调用时计算它们。
应保留公有接口不变(公有方法及其参数不变),但对私有部分,包括一些私有方法和实现进行修改。然后使用程序清单11.15对修改后的版本进行测试,结果应该与以前相同,因为Vector类的公有接口与原来的相同。
本题首先修改vector.h,将私有成员mag和ang删除,四个set函数删除,接着修改构造函数和reset()函数,修改完之后修改magval()和angvel()函数,最后修改一下友元输出函数,代码如下:
// vector1.h -- Vector class with <<, mode state
// store Vector use x and y
#ifndef VECTOR1_H_
#define VECTOR1_H_
#include <iostream>
namespace VECTOR
{
class Vector
{
public:
enum Mode{RECT, POL};
// RECT for rectangular, POL for Polar modes
private:
double x;
double y;
Mode mode;
// private methods for setting values;
public:
Vector();
Vector(double n1, double n2, Mode form = RECT);
void reset(double n1, double n2, Mode form = RECT);
~Vector();
double xval() const {return x;}
double yval() const {return y;}
double magval() const;
double angval() const;
void polar_mode(); // set mode to POL
void rect_mode(); // set mode to RECT
// oprator overloading
Vector operator+(const Vector & b) const;
Vector operator-(const Vector & b) const;
Vector operator-()const;
Vector operator*(double n) const;
// friends
friend Vector operator*(double n, const Vector & a);
friend std::ostream &
operator<<(std::ostream & os, const Vector & v);
};
} // end namespace VECTOR
#endif
// vector1.cpp -- methods for the Vector class
#include <cmath>
#include "vector1.h"
using std::sqrt;
using std::sin;
using std::cos;
using std::atan;
using std::atan2;
using std::cout;
namespace VECTOR
{
const double Rad_to_deg = 45.0/atan(1.0);
// should be about 57.2957795130823
Vector::Vector()
{
x = y = 0;
mode = RECT;
}
Vector::Vector(double n1, double n2, Mode form )
{
mode = form;
if(mode == RECT)
{
x = n1;
y = n2;
}
else if(mode == POL)
{
double ang = n2 / Rad_to_deg;
x = n1 * cos(ang);
y = n1 * sin(ang);
}
else
{
cout << "Incorrect 3rd argument to Vector() --";
cout << "vector set to 0\n";
x = y = 0;
mode = RECT;
}
}
// reset vector from rectangular cooridinates if form is
// RECT (the default) or else from polar coordinates if
// form is POL
void Vector::reset(double n1, double n2, Mode form)
{
mode = form;
if(mode == RECT)
{
x = n1;
y = n2;
}
else if(mode == POL)
{
double ang = n2 / Rad_to_deg;
x = n1 * cos(ang);
y = n1 * sin(ang);
}
else
{
cout << "Incorrect 3rd argument to Vector() --";
cout << "vector set to 0\n";
x = y = 0;
mode = RECT;
}
}
Vector::~Vector() // destructor
{
}
double Vector::magval() const
{
return sqrt(x * x + y * y);
}
double Vector::angval() const
{
if(x == 0.0 && y == 0.0)
return 0;
else
return atan2(y,x);
}
void Vector::polar_mode() // set to polar mode
{
mode = POL;
}
void Vector::rect_mode() // set to rect mode
{
mode = RECT;
}
// operator overloading
// add two Vectors
Vector Vector::operator+(const Vector & b) const
{
return Vector(x + b.x, y + b.y);
}
// subtract Vector b from a
Vector Vector::operator-(const Vector & b) const
{
return Vector(x - b.x, y - b.y);
}
// reverse sign of Vector
Vector Vector::operator-() const
{
return Vector(-x, -y);
}
// multiply vector by n
Vector Vector::operator*(double n) const
{
return Vector(n * x, n * y);
}
// friend methods
// mutiply n by Vector a
Vector operator*(double n, const Vector & a)
{
return a * n;
}
std::ostream & operator<<(std::ostream & os, const Vector & v)
{
if(v.mode == Vector::RECT)
os << "(x,y) = (" << v.x << ", " << v.y << ")";
else if(v.mode == Vector::POL)
{
os << "(m,a) = (" << v.magval() << ", " << v.angval() * Rad_to_deg << ")";
}
else
os << "Vector object mode is invalid";
return os;
}
} // end namespace VECTOR
运行结果如下:
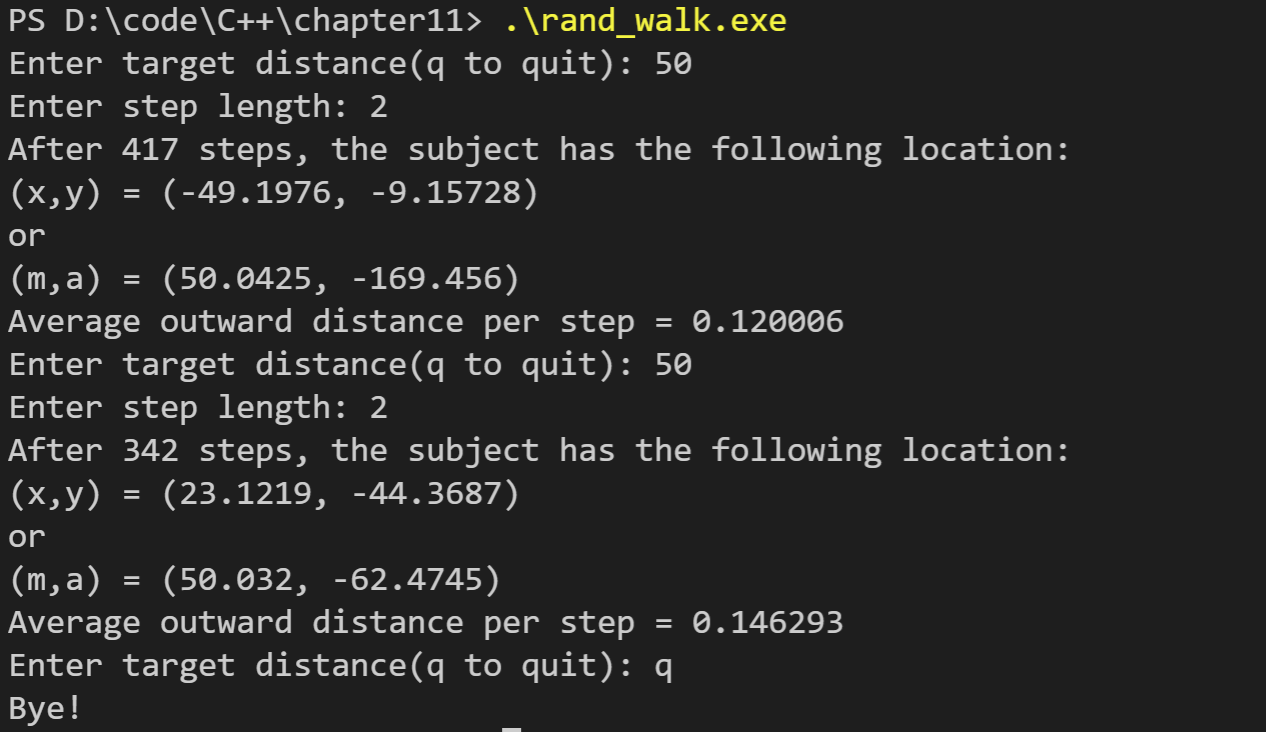
3. 修改程序清单11.15,使之报告N次测试中的最高、最低和平均步数(其中N是用户输入的整数),而不是报告每次的结果。
本题首先要定义一个数组,存储每次实验的结果,然后再写三个函数,计算数组的平均值、最小值和最大值,利用一个循环执行输入times次数的实验,注意需要初始化result,代码如下:
// ex3.cpp -- rand walk problem
// compile with the vect.cpp file
#include <cstdlib> // rand(), srand() protypes
#include <ctime> // time() protype
#include "vector1.h"
unsigned long average(unsigned long arr[],int n);
unsigned long findmax(unsigned long arr[],int n);
unsigned long findmin(unsigned long arr[],int n);
int main()
{
using namespace std;
using VECTOR::Vector;
srand(time(0)); // seed random-number generator
double direction;
Vector step;
Vector result(0.0, 0.0);
double target;
double dstep;
int times;
cout << "Enter target distance: ";
cin >> target;
cout << "Enter step length: ";
cin >> dstep;
cout << "Enter the times you want to test: ";
cin >> times;
unsigned long steps[times];
for(int i = 0; i < times; i++)
{
// initialize and reset result to 0
steps[i] = 0;
result.reset(0.0, 0.0); // is necessary
while(result.magval() < target)
{
direction = rand() % 360;
step.reset(dstep, direction, Vector::POL);
result = result + step;
steps[i]++;
}
}
unsigned long steps_max = findmax(steps, times);
unsigned long steps_min = findmin(steps, times);
unsigned long steps_ave = average(steps, times);
cout << "After " << times << " times test:\n";
cout << "Maximum steps is " << steps_max << endl;
cout << "Minimun steps is " << steps_min << endl;
cout << "Average steps is " << steps_ave << endl;
cout << "Bye!\n";
cin.clear();
while(cin.get() != '\n')
continue;
return 0;
}
unsigned long average(unsigned long arr[],int n)
{
unsigned long long sum = 0;
for(int i = 0; i < n; i++)
{
sum += arr[i];
}
return sum / n;
}
unsigned long findmax(unsigned long arr[],int n)
{
unsigned long max = 0;
for(int i = 0; i < n; i++)
max = max < arr[i] ? arr[i] : max;
return max;
}
unsigned long findmin(unsigned long arr[],int n)
{
unsigned long min = arr[0];
for(int i = 0; i < n; i++)
min = min < arr[i] ? min : arr[i];
return min;
}
运行结果如下:
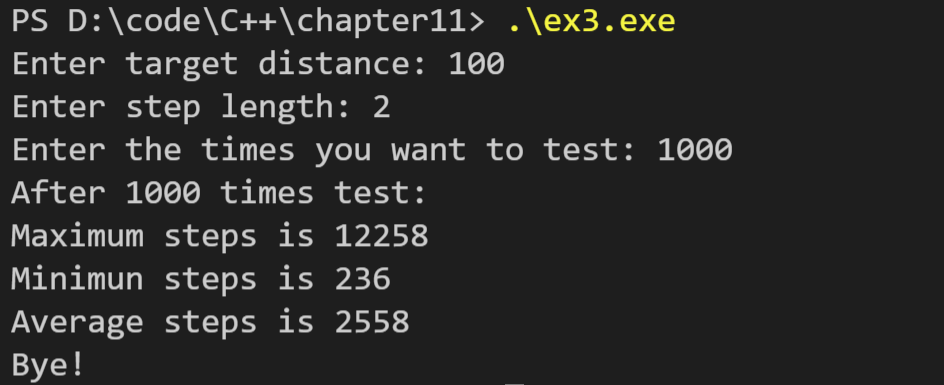
可以看到结果接近100/2的平方,因此是正确的。
4. 重新编写最后的Time类示例(程序清单11.10、程序清单11.11和程序清单11.12),使用友元函数来实现所有的重载运算符。
本题不算难,需要注意的是由于函数到了类外,因此函数不能声明为const的函数。需要修改程序11.10和程序11.11,类使用程序无需修改,程序如下:
// mytime.h -- Time class operator * and << overloading
#ifndef MYTIME_H_
#define MYTIME_H_
#include <iostream>
class Time
{
private:
int hours;
int minutes;
public:
Time();
Time(int h, int m = 0);
void AddMin(int m);
void AddHr(int h);
void Reset(int h = 0, int m = 0);
// friend
friend Time operator+(const Time & t1, const Time & t2);
friend Time operator-(const Time & t1, const Time & t2);
friend Time operator*(const Time & t, double n);
friend Time operator*(double n, const Time & t) {return t * n;}
friend std::ostream & operator<<(std::ostream & os,const Time & t);
};
#endif
// mytime.cpp -- implementing Time methods
#include <iostream>
#include "mytime.h"
Time::Time()
{
hours = minutes = 0;
}
Time::Time(int h, int m)
{
hours = h;
minutes = m;
}
void Time::AddMin(int m)
{
minutes += m;
if(minutes > 60)
{
hours += minutes / 60;
minutes %= 60;
}
}
void Time::AddHr(int h)
{
hours += h;
}
Time operator+(const Time & t1, const Time & t2)
{
Time sum;
sum.hours = t1.hours;
sum.minutes = t2.minutes;
sum.AddMin(t2.minutes);
sum.AddHr(t2.hours);
return sum;
}
Time operator-(const Time & t1, const Time & t2)
{
Time diff;
diff.minutes = t1.minutes - t2.minutes;
diff.hours = t1.hours - t2.hours;
if(diff.minutes < 0)
{
diff.minutes = 60 - diff.minutes;
diff.hours -= 1;
}
return diff;
}
Time operator*(const Time & t, double n)
{
Time result;
long totalminutes = (t.hours * 60 + t.minutes) * n;
result.minutes = totalminutes % 60;
result.hours = totalminutes / 60;
return result;
}
std::ostream & operator<<(std::ostream & os,const Time & t)
{
os << t.hours << " hours, " << t.minutes << " minutes";
return os; // is necessary
}
// usetime3_11_12.cpp -- using the third draft of the Time class
// compile usetime3.cpp and mytime0.cpp together
#include "mytime.h"
int main()
{
using std::cout;
using std::cin;
using std::endl;
Time weeding(4,35);
Time waxing(2,47);
Time total,diff,adjusted;
cout << "weeding time = " << weeding << endl;
cout << "waxing time = " << waxing << endl;
total = weeding + waxing;
cout << "total work time = " << total << endl;
diff = weeding - waxing;
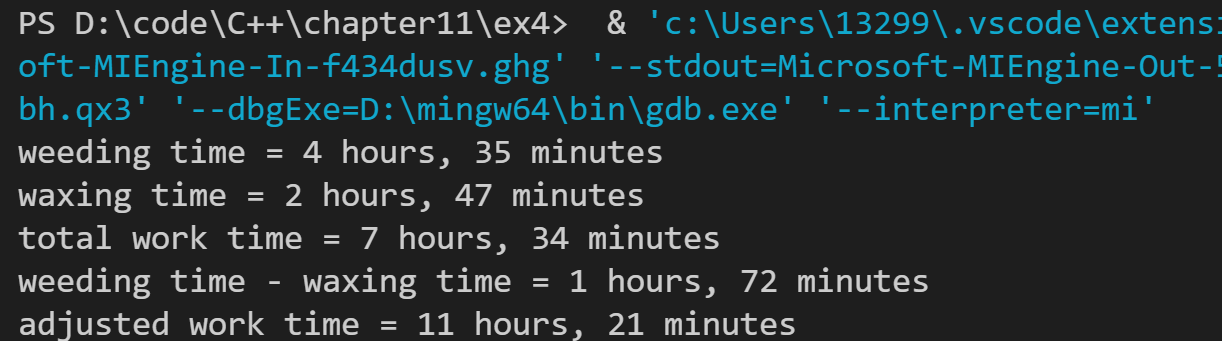
cout << "weeding time - waxing time = " << diff << endl;
adjusted = 1.5 * total;
cout << "adjusted work time = " << adjusted << endl;
return 0;
}
运行结果如下:
5. 重新编写Stonewt类(程序清单11.16和程序清单11.17),使它有一个状态成员,由该成员控制对象应转换为英石格式、整数磅格式还是浮点磅格式。重载<<运算符,使用它来替换show_stn()和show_lbs()方法。重载加法、减法和乘法运算符,以便可以对Stonewt值进行加、减、乘运算。编写一个使用所有类的小程序,来测试这个类。
本题有两种方式修改,一种是存储时,三种格式的数据都存储,利用mode来区分,需要那种格式的数据以对象成员调用即可;另一种方式是只选择一种格式存储,需要其他格式时,利用计算函数计算值返回。笔者采用的是第二种格式,编写过程中,构造函数遇到了问题,默认参数没有使用,导致出现了输出格式不正确的问题,加了mode = form之后解决,样例代码如下:
// stonewt.h -- definetion for the Stonewt class
#ifndef STONEWT_H_
#define STONEWT_H_
#include <iostream>
using std::ostream;
class Stonewt
{
public:
enum MODE {STONE, POUNDS, INT_POUNDS};
private:
enum{Lbs_per_stn = 14}; // pounds per stone
double pounds; // entire weight in pounds
MODE mode;
public:
Stonewt(double lbs, MODE form = POUNDS);
Stonewt(int stn, double lbs, MODE form = STONE);
Stonewt(int lbs, MODE form = INT_POUNDS);
Stonewt();
~Stonewt();
//get value
int stone_val() const;
double pds_left_val() const;
double pounds_val() const;
int int_pounds_val() const;
// set mode
void pounds_mode();
void int_pounds_mode();
void stone_mode();
// operator + - *
Stonewt operator+(const Stonewt & st) const;
Stonewt operator-(const Stonewt & st) const;
Stonewt operator*(double n) const;
//friend
// operator*
friend Stonewt operator*(double n, const Stonewt & st);
//operator<<
friend ostream & operator<<(ostream & os, const Stonewt & st);
};
#endif
// stonewt.cpp -- Stonewt methods
#include "stonewt.h"
// construct Stonewt object from double value
Stonewt::Stonewt(double lbs, MODE form)
{
mode = form; // is necessary
pounds = lbs;
}
// construct Stonewt object from stone, double values
Stonewt::Stonewt(int stn, double lbs, MODE form)
{
mode = form;
pounds = stn * Lbs_per_stn + lbs;
}
// construct Stonewt object form int pounds vlaue
Stonewt::Stonewt(int lbs, MODE form)
{
mode = form;
pounds = double(lbs);
}
// default constructor, wt = 0
Stonewt::Stonewt()
{
pounds = 0;
}
Stonewt::~Stonewt() // destructor
{
}
// get value
int Stonewt::stone_val() const
{
return int(pounds) / Lbs_per_stn;
}
double Stonewt::pds_left_val() const
{
return int(pounds) % Lbs_per_stn + pounds -int(pounds);
}
double Stonewt::pounds_val() const
{
return pounds;
}
int Stonewt::int_pounds_val() const
{
return int(pounds);
}
// set mode
void Stonewt::pounds_mode()
{
mode = POUNDS;
}
void Stonewt::int_pounds_mode()
{
mode = INT_POUNDS;
}
void Stonewt::stone_mode()
{
mode = STONE;
}
// operator + - *
Stonewt Stonewt::operator+(const Stonewt & st) const
{
return Stonewt(pounds + st.pounds);
}
Stonewt Stonewt::operator-(const Stonewt & st) const
{
return Stonewt(pounds - st.pounds);
}
Stonewt Stonewt::operator*(double n) const
{
return Stonewt(n * pounds);
}
// friend
Stonewt operator*(double n, const Stonewt & st)
{
return st * n;
}
ostream & operator<<(ostream & os, const Stonewt & st)
{
Stonewt::MODE mode;
mode = st.mode;
switch (mode)
{
case Stonewt::POUNDS:
os << "Double pounds: " << st.pounds << " pounds";
break;
case Stonewt::STONE:
os << "Stone: " <<st.stone_val() << " stone, " << st.pds_left_val() << " pounds";
break;
case Stonewt::INT_POUNDS:
os << "Int pounds: " << st.int_pounds_val() << " pounds";
break;
default:
os << "Stonewt object mode is invalid";
break;
}
}
// ex5_main.cpp -- test the Stonewt class
// compile with stonewt.cpp
#include "stonewt.h"
int main()
{
using std::cin;
using std::cout;
using std::endl;
double pounds;
int number; // the number of egg
Stonewt egg;
Stonewt weight;
egg = Stonewt(15.0);
cout << "Enter your weight in pounds: ";
cin >> pounds;
weight = Stonewt(pounds);
cout << "Before ate eggs, your weight:\n";
cout << weight << endl;
cout << "Enter the number of egg you eat: ";
cin >> number;
cout << "After ate " << number << " eggs, your weight:\n";
weight = weight + number * egg;
cout << weight << endl;
weight.stone_mode();
cout << weight << endl;
weight.int_pounds_mode();
cout << weight << endl;
return 0;
}
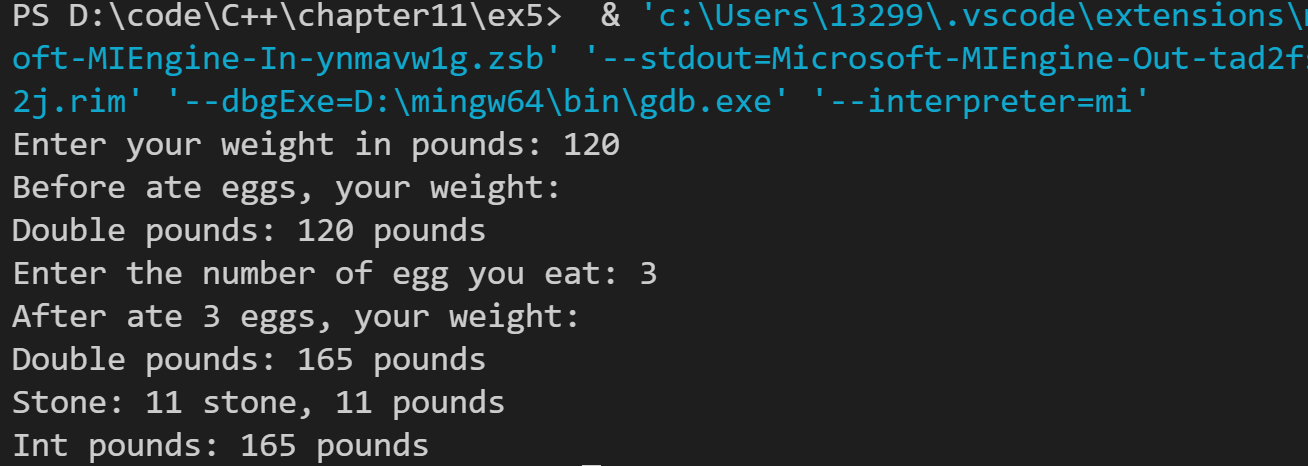
运行结果如下:
6. 重新编写Stonewt类(程序清单11.16和程序清单11.17),重载全部6个关系运算符。运算符对pounds成员进行比较,并返回一个bool值。编写一个程序,它声明一个包含6个Stonewt对象的数组,并在数组声明中初始化前三个对象,然后,使用循环来读取用于设置剩余三个数组元素的值。接着报告最小的元素,最大的元素,以及大于或等于11英石元素的数量(最简单的方法是创建一个Stonewt对象,并将其初始化为11英石,然后同其他对象进行比较)
本题考查的重载运算符函数的知识,可以采用友元函数或者成员函数进行重载,笔者采用了友元函数重载的方式,代码如下:
// stonewt.h -- definetion for the Stonewt class
#ifndef STONEWT_H_
#define STONEWT_H_
#include <iostream>
using std::ostream;
class Stonewt
{
public:
enum MODE {STONE, POUNDS, INT_POUNDS};
private:
enum{Lbs_per_stn = 14}; // pounds per stone
double pounds; // entire weight in pounds
MODE mode;
public:
Stonewt(double lbs, MODE form = POUNDS);
Stonewt(int stn, double lbs, MODE form = STONE);
Stonewt(int lbs, MODE form = INT_POUNDS);
Stonewt();
~Stonewt();
//get value
int stone_val() const;
double pds_left_val() const;
double pounds_val() const;
int int_pounds_val() const;
// set mode
void pounds_mode();
void int_pounds_mode();
void stone_mode();
// operator + - *
Stonewt operator+(const Stonewt & st) const;
Stonewt operator-(const Stonewt & st) const;
Stonewt operator*(double n) const;
//friend
// operator*
friend Stonewt operator*(double n, const Stonewt & st);
// oprator == != < > <= >=
friend bool operator==(const Stonewt & st1, const Stonewt & st2);
friend bool operator!=(const Stonewt & st1, const Stonewt & st2);
friend bool operator>(const Stonewt & st1, const Stonewt & st2);
friend bool operator<(const Stonewt & st1, const Stonewt & st2);
friend bool operator<=(const Stonewt & st1, const Stonewt & st2);
friend bool operator>=(const Stonewt & st1, const Stonewt & st2);
//operator<<
friend ostream & operator<<(ostream & os, const Stonewt & st);
};
#endif
// stonewt.cpp -- Stonewt methods
#include "stonewt.h"
// construct Stonewt object from double value
Stonewt::Stonewt(double lbs, MODE form)
{
mode = form; // is necessary
pounds = lbs;
}
// construct Stonewt object from stone, double values
Stonewt::Stonewt(int stn, double lbs, MODE form)
{
mode = form;
pounds = stn * Lbs_per_stn + lbs;
}
// construct Stonewt object form int pounds vlaue
Stonewt::Stonewt(int lbs, MODE form)
{
mode = form;
pounds = double(lbs);
}
// default constructor, wt = 0
Stonewt::Stonewt()
{
pounds = 0;
}
Stonewt::~Stonewt() // destructor
{
}
// get value
int Stonewt::stone_val() const
{
return int(pounds) / Lbs_per_stn;
}
double Stonewt::pds_left_val() const
{
return int(pounds) % Lbs_per_stn + pounds -int(pounds);
}
double Stonewt::pounds_val() const
{
return pounds;
}
int Stonewt::int_pounds_val() const
{
return int(pounds);
}
// set mode
void Stonewt::pounds_mode()
{
mode = POUNDS;
}
void Stonewt::int_pounds_mode()
{
mode = INT_POUNDS;
}
void Stonewt::stone_mode()
{
mode = STONE;
}
// operator + - *
Stonewt Stonewt::operator+(const Stonewt & st) const
{
return Stonewt(pounds + st.pounds);
}
Stonewt Stonewt::operator-(const Stonewt & st) const
{
return Stonewt(pounds - st.pounds);
}
Stonewt Stonewt::operator*(double n) const
{
return Stonewt(n * pounds);
}
// friend
Stonewt operator*(double n, const Stonewt & st)
{
return st * n;
}
bool operator==(const Stonewt & st1, const Stonewt & st2)
{
return st1.pounds == st2.pounds ? true : false;
}
bool operator!=(const Stonewt & st1, const Stonewt & st2)
{
return st1.pounds != st2.pounds ? true : false;
}
bool operator>(const Stonewt & st1, const Stonewt & st2)
{
return st1.pounds > st2.pounds ? true : false;
}
bool operator<(const Stonewt & st1, const Stonewt & st2)
{
return st1.pounds < st2.pounds ? true : false;
}
bool operator>=(const Stonewt & st1, const Stonewt & st2)
{
return st1.pounds >= st2.pounds ? true : false;
}
bool operator<=(const Stonewt & st1, const Stonewt & st2)
{
return st1.pounds <= st2.pounds ? true : false;
}
ostream & operator<<(ostream & os, const Stonewt & st)
{
Stonewt::MODE mode;
mode = st.mode;
switch (mode)
{
case Stonewt::POUNDS:
os << "Double pounds: " << st.pounds << " pounds";
break;
case Stonewt::STONE:
os << "Stone: " <<st.stone_val() << " stone, " << st.pds_left_val() << " pounds";
break;
case Stonewt::INT_POUNDS:
os << "Int pounds: " << st.int_pounds_val() << " pounds";
break;
default:
os << "Stonewt object mode is invalid";
break;
}
}
#include "stonewt.h"
int main()
{
const int Arsize = 6;
using std::cin;
using std::cout;
using std::endl;
double lbs;
Stonewt max;
Stonewt min;
int count = 0;
Stonewt starr[Arsize] = {
100,200,300
};
for(int i = 3; i < Arsize; i++)
{
cout << "Enter the weight in pounds: ";
cin >> lbs;
starr[i] = Stonewt(lbs);
}
cout << "Stonewt array list:\n";
for(int i = 0; i < Arsize; i++)
cout << starr[i] << endl;
cout << endl;
max = starr[0];
for(int i = 0; i < Arsize; i++)
{
max = max > starr[i] ? max : starr[i];
}
cout << "The maximum Stonewt object:\n" << max << endl;
min = starr[0];
for(int i = 0; i < Arsize; i++)
{
min = min < starr[i] ? min : starr[i];
}
cout << "The minimum Stonewt object:\n" << min << endl;
Stonewt st11 = Stonewt(11,0.0);
for(int i = 0; i < Arsize; i++)
{
if(starr[i] >= st11)
count++;
}
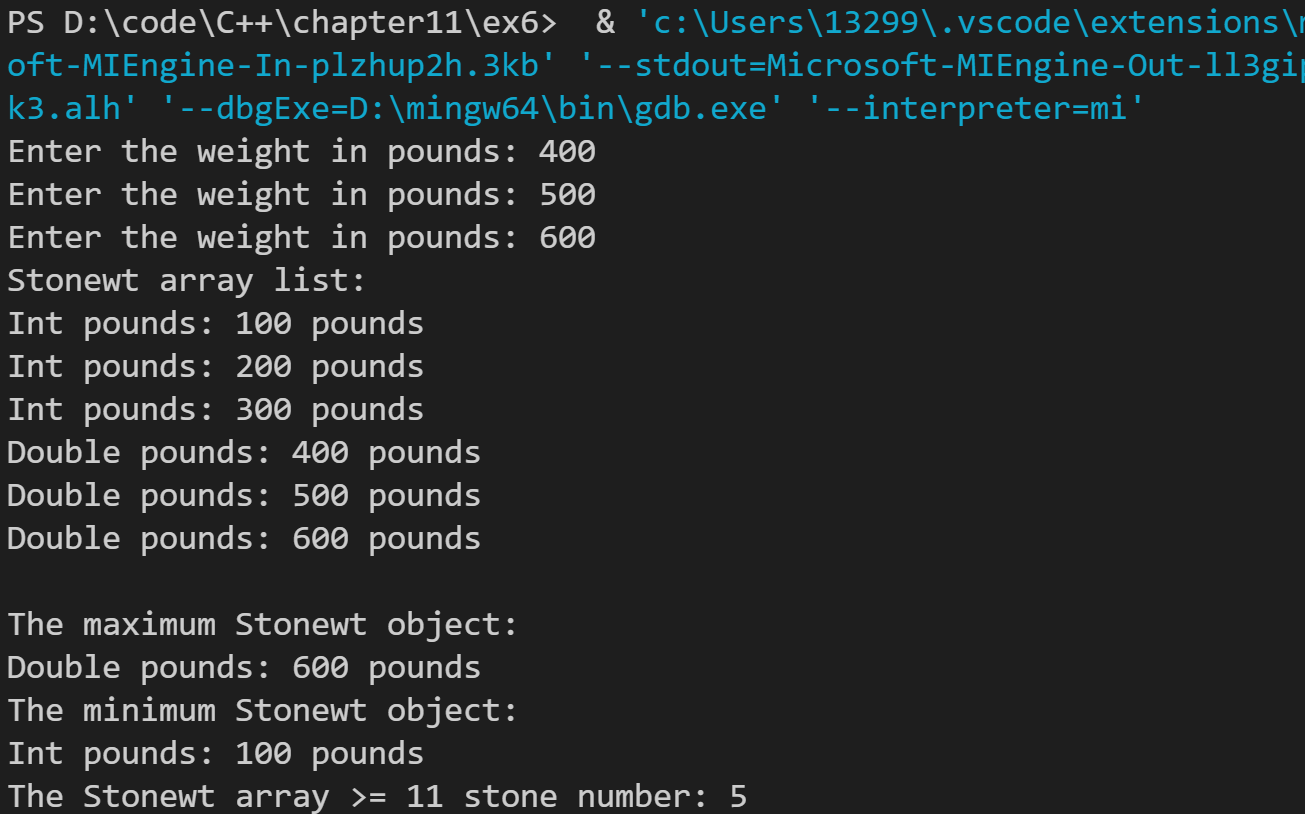
cout << "The Stonewt array >= 11 stone number: " << count << endl;
return 0;
}
运行结果如下:
7. 复数有两个部分组成:实数部分和虚数部分。复数的一种书写方式是:(3.0, 4.0),其中,3.0是实数部分,4.0是虚数部分。假设a = (A, Bi),c = (C,Di),则下面是一些复数计算。
- 加法:a + c = (A + C, (B + D)i)
- 减法:a - c = (A - C, (B - D)i)
- 乘法:a * c = (AC-BD,(AD+BC)i)
- 乘法::x c = (xC,x*Di),其中x为实数
- 共轭: ~a = (A,-Bi)
请定义一个复数类,以便下面的程序可以使用它来获得正确的结果。
#include <iostream>
using namespace std;
#include "complex0.h" // to avoid confusion with complex.h
int main()
{
complex a(3.0, 4.0);
complex c;
cout << "Enter a complex number(q to quit):\n";
while(cin >> c)
{
cout << "c is " << c << '\n';
cout << "complex conjugate is " << ~c << '\n';
cout << "a is " << a << '\n';
cout << "a + c is " << a + c << '\n';
cout << "a - c is " << a - c << '\n';
cout << "a * c is " << a * c << '\n';
cout << "2 * c is " << 2 * c << '\n';
cout << "Enter a complex number(q to quit):\n"
}
cout << "Done!\n";
return 0;
}
注意,必须重载运算符<<和>>。标准C++使用头文件complex提供了比这个示例更广泛的复数支持,因此应将自定义的头文件命名为complex0.h,以免发生冲突,应尽可能使用const。
下面是该程序的运行情况。
Enter a complex number(q to quit):
real: 10
imaginary: 12
c is (10, 12i)
complex conjugate is (10, -12i)a is (3, 4i)a + c is (13, 16i)
a - c is (-7, -8i)
a * c is (-18, 76i)
2 * c is (20, 24i)
Enter a complex number(q to quit):
real: q
Done!
请注意,经过重载后,cin>>c将提示用户输入实数和虚数部分。
本题不算难实现上,对于加减乘运算,采用的是成员函数运算符重载,对于输出,之前输出过,因此没什么大问题,对于输入,重载函数定义时忘了输入不能用const引用,因此刚开始提示错误了,后面修改完善了,输入q离开刚开始没做处理,因此会输出imaginar:后面用if语句解决。
代码如下:
// complex0.h -- defination of complex class
#ifndef COMPLEX0_H_
#define COMPLEX0_H_
#include <iostream>
using std::ostream;
using std::istream;
class complex
{
private:
double real;
double imaginary;
public:
complex(double i, double j);
complex();
~complex();
// overloading operator + - * and ~
complex operator+(const complex & c) const;
complex operator-(const complex & c) const;
complex operator*(const complex & c) const;
complex operator~() const;
// friend
friend complex operator*(double n, const complex & c);
friend istream & operator>>(istream & os, complex & c);
friend ostream & operator<<(ostream & os, const complex & c);
};
#endif
// complex0.cpp -- methods for complex class
#include "complex0.h"
// constructor
complex::complex(double i, double j)
{
real = i;
imaginary = j;
}
complex::complex() // default
{
real = imaginary = 0.0;
}
// deconstructor
complex::~complex()
{
}
// overloading operator
complex complex::operator+(const complex & c) const
{
return complex(real + c.real, imaginary + c.imaginary);
}
complex complex::operator-(const complex & c) const
{
return complex(real - c.real, imaginary - c.imaginary);
}
complex complex::operator*(const complex & c) const
{
return complex(real * c.real - imaginary * c.imaginary, real * c.imaginary + imaginary * c.real);
}
complex complex::operator~() const
{
return complex(real, -imaginary);
}
// friend
complex operator*(double n, const complex & c)
{
return complex(n * c.real, n * c.imaginary);
}
std::istream & operator>>(std::istream & is, complex & c)
{
std::cout << "real: ";
if(is >> c.real)
{
std::cout << "imaginary: ";
is >> c.imaginary;
}
return is;
}
std::ostream & operator<<(std::ostream & os, const complex & c)
{
os << "(" << c.real << ", " << c.imaginary << "i)";
return os;
}
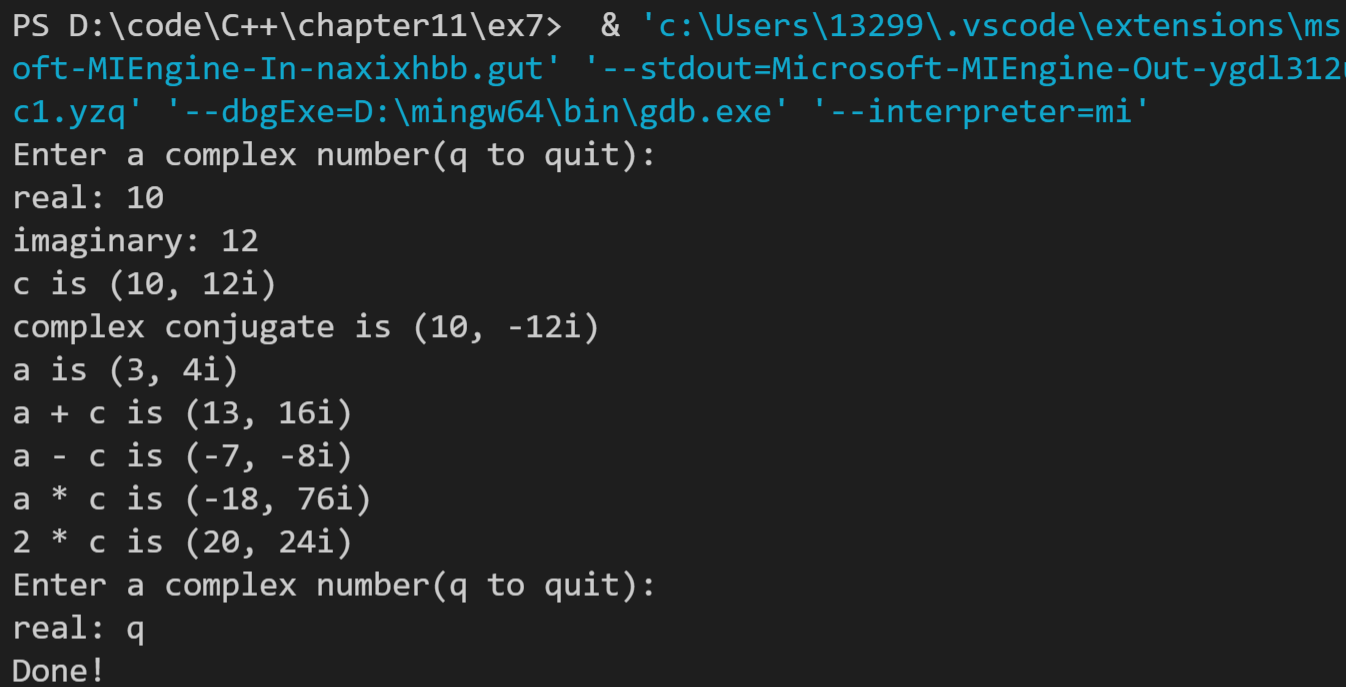
运行结果如下:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号