P6071 MDOI TreeQuery（主席树 And 虚树 Or 主席树 And 倍增）

『MdOI R1』Treequery

前置知识：主席树，虚树，倍增，最近公共祖先

题目描述

给定一棵 \(n\) 个点的无根树，边有边权。

令 \(E(x,y)\) 表示树上 \(x,y\) 之间的简单路径上的所有边的集合，特别地，当 \(x=y\) 时，\(E(x,y) = \varnothing\)。

你需要实时回答 \(q\) 个询问，每个询问给定 \(p,l,r\)，请你求出集合 \(\bigcap_{i=l}^r E(p,i)\) 中所有边的边权和，即 \(E(p, l\dots r)\) 的交所包含的边的边权和。

通俗的讲，你需要求出 \(p\) 到 \([l,r]\) 内每一个点的简单路径的公共部分长度。

输入格式

第一行两个整数 \(n,q\)，表示树的结点数和询问数。

接下来 \(n-1\) 行，每行三个整数 \(x,y,w\)，表示 \(x\) 与 \(y\) 之间有一条权值为 \(w\) 的边。

接下来 \(q\) 行，每行三个整数 \(p_0,l_0,r_0\)。第 \(i\) 个询问的 \(p,l,r\) 分别为 \(p_0,l_0,r_0\) 异或上 \(lastans\) 的值，其中 \(lastans\) 是上次询问的答案，初始时为 \(0\)。

对于 \(100\%\) 的数据，\(1\leq n,q\leq 2\times 10^5\)，\(1\leq x,y,p\leq n\)，\(1\leq l\leq r\leq n\)，\(1\leq w\leq 10^4\)。

Solution

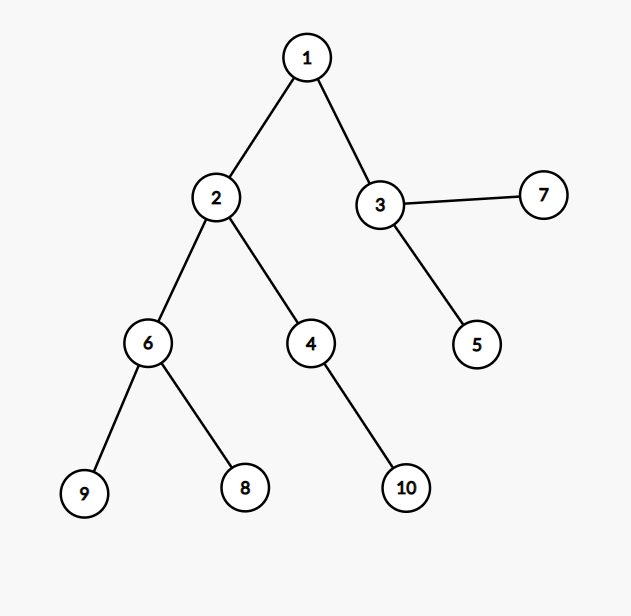
首先分析一下会有哪些情况

\([l\,, r]\)内的节点都在\(p\)的子树之内
- 选择\(p = 1, l = 8, r = 10\)，观察可知此时路径应为\(1 \rightarrow 2\)。
\([l\,,r]\)的节点部分在\(p\)的子树内
- 选择\(p = 1,\,l = 2,\, r = 10\)，观察可知此时答案应该为0。
\([l\,,r]\)的节点都在\(p\)的子树外）
- 如果选择\(p = 9,\,l = 1,\, r = 6\)，此时答案路径为\(6 \rightarrow 9\)
- 如果选择\(p = 9,\,l = 4,\, r = 4\)，此时答案路径为\(2 \rightarrow 6 \rightarrow 9\)，与上一种情况很像，但又似乎不太一样？

如果懂一点虚树

如果我们能够将\([l \cdots r]\)这些点构建成一颗虚树，那只要\(p\)不在这颗虚树之内，那答案一定就是一条从\(p \rightarrow virtualtree\)的路径

再分别深入思考一下

第一种情况，我们能很主观的感觉到答案应为\(lca(l \cdots r) \rightarrow p\)的路径长度。
- 解释：此时我们从p点往下走向\([l \cdots r]\)每一个点，很显然当路径第一次出现分叉（即进入两颗不同的子树）之前的路径应该都是算入答案的，那这个点就是\([l \cdots r]\)这些点的lca，这是符合lca的定义的。
- 做法：那此时我们想知道答案我们只需求出\([l \cdots r]\)的lca，这是在求一个点集的lca
求一个点集的lca：

先假设这个点集的lca为L

想一下dfn序这个东西，一个子树内的dfn序是连续的，可以记录下出点和入点来把一个子树表示成一个区间，那我们考虑这个子树中的一个子树，他的dfn序一定也是连续的，所以子树和子树的子树其实就是区间中的一个小区间，那么这个点集一定是在L的子树内部的，一定可以表示成离散的点或者连续的线段。比方说我们有两个点在下图的1和2区间内，那他们的lca一定是他们外部第一个黄色区间的左端点，所以我们要找到一个点集的lca只要找到这个点集中dfn最小和最大的两个点（即由这些离散的点或者连续的线段形成的区间的最左侧和最右侧区间端点，从而保证外部的第一个大区间一定包含了这个点集，也就是说保证了在L的子树内部）~~纯口胡希望能懂~~ 好好理解一下，下面要考的
- 所以我们只要把得到点集的最小最大dfn然后求一个lca，那么答案就是
  \[ans\_situation1 = dis[p \rightarrow lca(\min(dfn[l \cdots r]))), \max(dfn[l\cdots r])] \]
第二种情况的答案是很显然的，必然存在一条走向子树的路径和走向子树之外的路径这两条路径的交集一定为\(\varnothing\)

\[ans\_situation2 = 0 \]
第三种情况最为复杂，可以想象因为都在\(p\)的子树外面所以这些路径一定是以\(p \rightarrow fa(p)\)为起点的
- 对于第一种子情况，也就是\(p \rightarrow root\)这个路径上有\([l \cdots r]\)的点的时候答案一定是
\[ans\_sitiuation3\cdot1 = dis[p \rightarrow \max depth[k]](k \in [l \cdots r] \;and\; k \in path[p\rightarrow fa(p)]) \]
- 对于第二种子情况，也就是\(p \rightarrow root\)这个路径上没有\([l \cdots r]\)的点的时候，换而言之\([l \cdots r]\)在一棵不含\(p\)的子树内部，那这时候答案其实是和情况一是相同的
  \[ans\_situation3 \cdot 2 = dis[p \rightarrow lca(\min(dfn[l \cdots r]))), \max(dfn[l\cdots r])] \]

最后考虑如何计算

我们需要计算的有这些东西：

\[1. dis[path]\;\\ 2.lca(set)\;\\ 3.\max depth[k]](k \in [l \cdots r] \;and\; k \in path[p\rightarrow fa(p)] \]

对于第一个距离我们可以处理一个树上前缀和\(pre[]\)我们要获取一段路径的距离只需差分即可，对于上述三种情况的答案全都可以转化为以下的式子，当然有两种情况我们可以发现这个式子可以进行适当的化简

\[ans = pre[p] + pre[lca(l\cdots r)] - 2 * pre[lca(p, lac(l \cdots r))] \]
对于一个集合的lca我们之前已经提到过，我们只需找到集合中的\(\min dfn[l\cdots r] \; and \;\max dfn[l\cdots r]\)即可，再想一下虚树的理论，发现我们要快速得到一个只含\([l\cdots r]\)的点集，然后在对\(dfn\)进行求\(min \; max\)的操作，应该能发现这是一个二维数点问题，可以用主席树维护，只要按照点的标号为根节点(本质上是二维平面中的一个轴，主席树通过前缀和压缩了这个轴)，再以\(dfn\)为权值。
对于第三个东西，用人话说就是我们要找\(p\)往上走遇到的第一个\([l \cdots r]\)以内的点，一个很直观的做法就是直接倍增，利用主席树判断我们有没有找到，具体的找法就是每次找到一个点之后判断这个子树是不是只含有\(p\)不包含\([l \cdots r]\)中任何一个点，找到我们就往上跳，跳到最上方为止，那么该点的父节点应该就是我们要找的点。这个做法复杂度为\(\log^2n\)的，能过，但是我们有更好的做法。我们要求的点其实是\(lca(p, [l\cdots r])\)中深度最大的点，在上文说到过\(dfn\)是一个具有区间性质的东西，求\(lca\)有一种\(ST\)表的做法就揭示了\(dfn\)其实具有某种单调性，如果我们把\(p\)这个点也放到这个点集内，我们站在\(dfn\)的轴上观察这些点，我们考虑\(p\)的左侧的第一个点和第二个点，令他们分别为\(k1, k2\)，通过\(dfn\)求点集\(lca\)的做法我们能够知道

\[lca(k1, p) \in subtree(k2) \Longrightarrow depth[lca(k1, p)] > depth[lca(k2, p)] \]
所以我们找到\([l, r]\)点集内部\(p\)左右两侧的两个点，求\(p\)和这两个点的\(lca\)然后根据深度取\(max\)或者答案取\(min\)即可
我们再来捋一下这棵主席树要处理那些信息以及对于上述三种情况的判断
1. 如上文所说，我们构建的主席树的结构应该是以点的标号为根节点，再以\(dfn\)为权值，\(1\)表示这个点存在，\(0\)表示点不存在。此时我们要判断\([l\cdots r]\)是否在\(p\)的子树内部我们只要判断主席树上\([l \cdots r]\)内部\(in[p] \le dfn \le out[p]\)的和是否为\(r - l + 1\)即可，如果为\(0\)则为情况二，否则为情况三。
2. 如果要判断情况三的两种子情况，我们只要判断\(lca(l\cdots r)== lca(p, lca(l\cdots r))\)即可，相等为第一种子情况。
3. 还要查询一个某个点的左侧最大值和右侧最小值，以及整个区间内的最大最小值，我们可以写成一个主席树区间查询权值区间第k大，要采用线段树上二分的方式（大概也是整个题目最难实现的地方，但好像也还好），我是写了两个区间查询单点左侧最大值和右侧最小值。
4. \(lca\)可以采取\(st\)表或者倍增，自测差不多，或许树剖会更快，总复杂度\(O(n\log n)\)。

CODE

int n, q;
int rt[maxn << 5], ls[maxn << 5], rs[maxn << 5], cnt[maxn << 5], idx;
void update(int rtu, int &rtv, int l, int r, int pos) {
    rtv = ++idx;
    ls[rtv] = ls[rtu], rs[rtv] = rs[rtu], cnt[rtv] = cnt[rtu];
    if (l == r) {
        cnt[rtv]++;
        return ;
    }
    int mid = l + r >> 1;
    if (pos <= mid) update(ls[rtu], ls[rtv], l, mid, pos);
    else update(rs[rtu], rs[rtv], mid + 1, r, pos);
    cnt[rtv] = cnt[ls[rtv]] + cnt[rs[rtv]];
}

int query_sum(int rtu, int rtv, int l, int r, int ql, int qr) {
    if (ql <= l && r <= qr) return cnt[rtv] - cnt[rtu];
    int mid = l + r >> 1;
    int ans = 0;
    if (ql <= mid) ans += query_sum(ls[rtu], ls[rtv], l, mid, ql, qr);
    if (mid < qr) ans += query_sum(rs[rtu], rs[rtv], mid + 1, r, ql, qr);
    return ans;
}

int query_mx(int rtu, int rtv, int l, int r, int pos) {
    if (l > pos || cnt[rtv] - cnt[rtu] == 0) return 0;
    if (l == r) return l;
    int mid = l + r >> 1;
    if (mid >= pos) return query_mx(ls[rtu], ls[rtv], l, mid, pos);
    int res = cnt[rs[rtv] - cnt[rs[rtu]]];
    int ans = 0;
    if (res) ans = query_mx(rs[rtu], rs[rtv], mid + 1, r, pos);
    if (!ans) ans = query_mx(ls[rtu], ls[rtv], l, mid, pos);
    return ans;
}

int query_mn(int rtu, int rtv, int l, int r, int pos) {
    if (r < pos || cnt[rtv] - cnt[rtu] == 0) return n + 1;
    if (l == r) return l;
    int mid = l + r >> 1;
    if (mid < pos) return query_mn(rs[rtu], rs[rtv], mid + 1, r, pos);
    int res = cnt[ls[rtv] - cnt[ls[rtu]]];
    int ans = n + 1;
    if (res) ans = query_mn(ls[rtu], ls[rtv], l, mid, pos);
    if (ans == n + 1) ans = query_mn(rs[rtu], rs[rtv], mid + 1, r, pos);
    return ans;
}

vector<pii> e[maxn];
int fa[maxn][19];
int DFN, in[maxn], out[maxn], ID[maxn];
int dep[maxn << 1], pre[maxn];
void dfs(int u, int p) {
    in[u] = ++DFN;
    ID[DFN] = u;
    fa[u][0] = p;
    dep[u] = dep[p] + 1;
    for (auto [v, w] : e[u])
        if (v != p) {
            pre[v] = pre[u] + w;
            dfs(v, u);
        }
    out[u] = DFN;
}

void init_lca(int n) {
    for (int j = 1; j < 19; ++j)
        for (int i = 1; i <= n; ++i)
            fa[i][j] = fa[fa[i][j - 1]][j - 1];
}
int get_lca(int u, int v) {
    if (dep[u] > dep[v]) swap(u, v);
    for (int i = 18; i >= 0; --i)
        if (dep[v] - dep[u] >= (1 << i))
            v = fa[v][i];
    if (u == v) return u;
    for (int i = 18; i >= 0; --i)
        if (fa[u][i] != fa[v][i])
            u = fa[u][i], v = fa[v][i];
    return fa[u][0];
}


void solve(int cas) {
    cin >> n >> q;
    for (int i = 1; i < n; ++i) {
        int u, v, w; cin >> u >> v >> w;
        e[u].eb(v, w); e[v].eb(u, w);
    }
    dfs(1, 0); init_lca(n);
    for (int i = 1; i <= n; ++i) {
        update(rt[i - 1], rt[i], 1, n, in[i]);
    }
    int lasAns = 0;
    while (q--) {
        int p, l, r; cin >> p >> l >> r;
        p ^= lasAns, l ^= lasAns, r ^= lasAns;
        int res = query_sum(rt[l - 1], rt[r], 1, n, in[p], out[p]);
        if (res == r - l + 1) {
            int lo = ID[query_mn(rt[l - 1], rt[r], 1, n, 1)];
            int hi = ID[query_mx(rt[l - 1], rt[r], 1, n, n)];
            int lca = get_lca(lo, hi);
            cout << (lasAns = pre[lca] - pre[p]) << '\n';
        } else if (res) {
            cout << (lasAns = 0) << '\n';
        } else {
            int lo = ID[query_mn(rt[l - 1], rt[r], 1, n, 1)];
            int hi = ID[query_mx(rt[l - 1], rt[r], 1, n, n)];
            int lca = get_lca(lo, hi);
            if (get_lca(lca, p) == lca) {
                int pr = ID[query_mx(rt[l - 1], rt[r], 1, n, in[p] - 1)];
                int su = ID[query_mn(rt[l - 1], rt[r], 1, n, in[p] + 1)];
                int ans = INF;
                if (pr) ans = min(ans, pre[p] - pre[get_lca(pr, p)]);
                if (su) ans = min(ans, pre[p] - pre[get_lca(su, p)]);
                cout << (lasAns = ans) << '\n';
            } else {
                cout << (lasAns = pre[p] + pre[lca] - 2 * pre[get_lca(lca, p)]) << '\n';
            }
        }
    }
}

posted @ 2023-04-04 23:58 Fighoh 阅读(46) 评论(0) 编辑收藏举报

刷新页面返回顶部

Fighoh