基础树形结构
树形结构指的是数据元素之间存在着“一对多”的树形关系的数据结构,是一类重要的非线性数据结构。 ——百度百科
1. 树的性质与遍历
1.1 树的性质
树是一个 个节点, 条边的无向连通图。
每一个节点有一个父亲节点,若 为 的父亲节点,则 为 的子节点。
深度相同的节点被称为兄弟节点。
如果钦定一个点作为整棵树的根,这就被称为一棵有根树,否则被称为一棵无根树。
注:根节点即树中唯一一个没有父亲节点的节点。
1.2 树的遍历
例题:P5908 猫猫和企鹅
题目大意:
王国里有 个居住区,它们之间有 条道路相连,并且保证从每个居住区出发都可以到达任何一个居住区,并且每条道路的长度都为 。
每个居住区住着一个小企鹅,有一天一只猫猫从 号居民区出发,想要去拜访一些小企鹅。可是猫猫非常的懒,它只愿意去距离它在 以内的小企鹅们。
猫猫非常的懒,因此希望你告诉他,他可以拜访多少只小企鹅。
对于 的数据,。
树的存储与无向图的存储类似,一般我们用链式前向星或者 存储,如果知道父亲节点与儿子节点的关系,可以用有向图的存储方式;否则应当存储双向边。
树的遍历最常用的是 dfs,核心代码如下:
void dfs(int u, int fa) { // u 为当前节点,fa 为父亲节点
for (auto v : G[u]) { // v 为 u 的儿子节点
if (v == fa) continue; // 因为存的是双向边,所以应该判断是否是自己的父亲节点
dfs(v, u);
}
}
设 表示节点 的深度,那么这道题就是求 的节点的数量。
但是树的遍历还可以用 bfs,虽然并不常用,这里给出核心代码:
queue <int> q;
int fa[N];
void bfs(int root) {
q.push(root); fa[root] = 0;
while (!q.empty()) {
int now = q.front(); q.pop();
for (auto v : G[now]) {
if (v == fa[now]) continue;
fa[v] = now;
q.push(v);
}
}
}
有许多树有特殊的形态,常作为题目中特殊性质的部分分出现。
-
链:每一个节点除了叶子节点只有一个子节点。
-
菊花图:除了根节点外的所有节点都向根节点连边。
2. 树的直径与重心
2.1 树的直径
设一条边的边权为 ,定义
也就是节点 到节点 之间的距离为 到 简单路径上的边权之和。
一棵树的直径就是两点之间距离的最大值,也就是
求直径的常用方法有两种——两遍 dfs 法和树形 dp,这里仅介绍两遍 dfs 法。
两遍 dfs 法是比较推荐的(主要是考场上不容易忘),时间复杂度 。
两遍 dfs 法的流程:
-
随意选择一个节点 作为起点,进行第一遍 dfs,找出距离 最远的节点 。
-
以 为起点,进行第二遍 dfs,找出距离 最远的节点 。
-
则 和 就是直径的两个端点。
具体证明可以看一下这篇 Blog。
注意点:两遍 dfs 法无法处理负边权的情况。
题目大意:
给定一棵 个节点的无根树,边带权,定义一段路径 的偏心距 为树中距离路径 最远的节点到路径 的距离。
找到一段路径 ,满足 是树的直径上的一段,长度不超过 ,且 最小,输出这个最小值。
原题数据范围:。
稍稍膜改后的数据范围:。
首先我们肯定是要把树的直径求出来的,然后我们考虑这个最小的偏心距怎么求?
首先我们方便起见,以直径的一个端点为根节点。
那么对于所有的节点,我们可以求出不经过直径上的其它点所能够到达的最远距离。
我们考虑一段路径的偏心距怎么算。
考虑这样一张图:
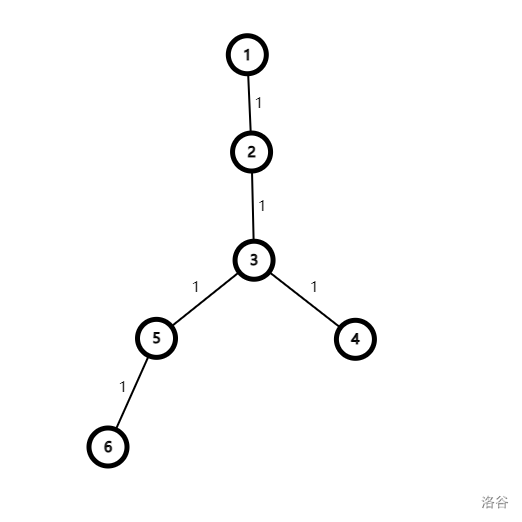
很明显,直径为从节点 到节点 的路径。
我们可以求出对于每一个点,不经过直径上其它点的情况下能够到达的最远的距离 ,显然,因为除了根节点,每一个直径上的节点的父亲节点也是直径上的,所以我们只需要考虑子树内的贡献即可。
引理 1
对于直径上的任意一个点 ,到它的距离最远的点一定是两个端点之一。
证明:
设两个端点分别为 和 ,有一个点 使得 ,那么就可以用 和 组成一条更长的路径,不符合直径的定义,原题得证。
所以我们就可以用双指针维护一段长度不超过 的直径上的路径。
然后这条路径的偏心距就是除了两个端点之外的点的 值中最大值和路径两个端点分别到直径两个端点的距离取 即可。
除了两个端点之外的点的 值中最大值可以用单调队列维护。
时间复杂度 。
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 5;
int n, s;
vector < pair <int, int> > G[N];
int A, B, dis[N], far = 0, f[N], father[N];
bool flag[N] = {false};
int q[N], head, tail, ans;
static inline
void dfs(int u, int fa) {
if (dis[u] > dis[far]) far = u;
for (auto v : G[u]) {
if (v.first == fa) continue;
father[ v.first ] = u;
dis[ v.first ] = dis[u] + v.second;
dfs(v.first, u);
}
}
void dfs2(int u, int fa) {
for (auto v : G[u]) {
if (v.first == fa) continue;
dfs2(v.first, u);
if (!flag[ v.first ]) f[u] = max(f[u], f[ v.first ] + v.second);
}
}
void add(int x, int limit) {
while (head <= tail && dis[ q[head] ] >= dis[limit]) head++;
while (head <= tail && f[ q[tail] ] <= f[x]) tail--;
q[ ++tail ] = x;
}
int QueryMax() {
return f[ q[head] ];
}
int main() {
scanf("%d%d", &n, &s);
for (int i = 1; i < n; i++) {
int u, v, w; scanf("%d%d%d", &u, &v, &w);
G[u].push_back({v, w});
G[v].push_back({u, w});
}
dis[1] = 0; dfs(1, 0); A = far;
dis[A] = father[A] = 0; far = 0; dfs(A, 0); B = far;
for (int i = B; i; i = father[i]) flag[i] = true;
dfs2(A, 0);
int l = B, r = B; ans = dis[B]; head = 1; tail = 0;
while (r) {
while (dis[r] - dis[ father[l] ] <= s && l) {
add(l, r);
l = father[l];
int now = max(QueryMax(), max(dis[B] - dis[r], dis[l]));
ans = min(ans, now);
}
r = father[r];
}
printf("%d\n", ans);
return 0;
}
双倍经验:P2491 [SDOI2011] 消防
2.2 树的重心
树的重心就是一个节点 ,使得以 为根时,最小化
或者一个节点 ,使得以 为根时,
从重心的这条结论中,我们能够推出重心的 条性质:
- 以重心为根时,所有子树的大小不超过全树大小的一半。
这是一条挺重要的性质,也是重心的第二条定义,点分治就主要时运用这条性质实现 的。
- 树中所有点到某个点的距离和中,到重心的距离和是最小的;如果有两个重心,那么到它们的距离和一样。
这条性质证明挺简单的,我们考虑最优的节点从重心移动,那么子树内的所有节点贡献 ,子树外的所有节点贡献 ,因为以重心为根时,所有子树的大小不超过全树大小的一半,所以加上的肯定比减去的多,易证重心为最优节点。
- 把两棵树通过一条边相连得到一棵新的树,那么新的树的重心在连接原来两棵树的重心的路径上。
- 在一棵树上添加或删除一个叶子,那么它的重心最多只移动一条边的距离。
如果添加或删除一个叶子节点,最多使一棵子树内的节点数量比一半多 ,移动一次重心即可解决问题。
那么如何求重心?
这个其实很简单,只需要进行一遍 dfs,求出每一个 表示以 为根的子树的大小,根据定义求解即可。
int siz[N], f[N], root(0); // root 表示重心
void dfs(int u, int fa) {
siz[u] = 1;
for (auto v : G[u]) {
if (v == fa) continue;
dfs(v, u); siz[u] += siz[v];
f[u] = max(f[u], siz[v]);
}
f[u] = max(f[u], n - siz[u]); // 别忘记把子树外的贡献算上
if (!root || f[u] < f[root]) root = u;
}
例题:P1395 会议
题目大意:
给定一棵 个节点的树,求出一个节点使得所有节点到这个节点的距离之和最小,输出节点编号以及最小值,如果有多个节点符合要求,输出编号最小的那一个。
对于 的数据,。
根据重心的性质 ,求出重心之后再求一个距离之和,然后就没有然后了……
代码应该不用放了。
这道题还有一种换根 dp 的做法,也是 的,这就不需要推重心的性质。
这里放一下代码,有兴趣的同学可以学习一下:
#include <bits/stdc++.h>
using namespace std;
const int N = 5e4 + 5;
const int inf = 1e9;
int n, f[N], siz[N];
vector <int> G[N];
void dfs1(int u, int fa, int dis) {
f[1] += dis; siz[u] = 1;
for (auto v : G[u]) {
if (v == fa) continue;
dfs1(v, u, dis + 1); siz[u] += siz[v];
}
}
void dfs2(int u, int fa) {
for (auto v : G[u]) {
if (v == fa) continue;
f[v] = f[u] - siz[v] + n - siz[v];
dfs2(v, u);
}
}
int main() {
scanf("%d", &n);
for (int i = 1; i < n; i++) {
int u, v; scanf("%d%d", &u, &v);
G[u].push_back(v); G[v].push_back(u);
}
dfs1(1, 0, 0);
dfs2(1, 0);
int ans(0); f[0] = inf;
for (int i = 1; i <= n; i++) {
if (f[ans] > f[i]) ans = i;
}
printf("%d %d\n", ans, f[ans]);
return 0;
}
3. 最近公共祖先
最近公共祖先,也被称为 LCA(Lowest Common Ancestor)。
对于有根树 的两个结点 ,最近公共祖先 表示一个结点 ,满足 是 和 的祖先且 的深度尽可能大。在这里,一个节点也可以是它自己的祖先。 ——百度百科
题目大意:
给定一棵 个节点,以节点 为根的树,有 个询问,每次询问 的 LCA。
对于 的数据,。
3.1 Brute Force 算法
人类历史上最优美的算法 (逃
假如数据范围只有 怎么做?
肯定是暴力往上跳啊!
我们就有一个显而易见的算法,先把节点 往上跳到同一高度,然后往上跳,直到跳到同一个节点,即为 LCA。
inline int LCA(int x, int y) {
if (dep[x] < dep[y]) swap(x, y);
while (dep[x] > dep[y]) x = fa[x];
if (x == y) return x;
while (x != y) x = fa[x], y = fa[y];
return x;
}
显然时间复杂度是 的,过不了 的数据。
3.2 倍增算法
既然一个一个往上跳太慢了,为什么不直接往上跳多步呢?
于是借鉴倍增的思想,对于一个数 ,进行二进制拆分,必然能够拆分成如下形式:
且 ,满足 。
所以我们可以记录 表示从节点 开始往上跳 个节点所到达的节点。
这样我们就最多只需要跳 次即可。
我们接下来考虑 的状态转移方程,显然往上跳 个节点可以转换为先往上跳 个节点,再往上跳 个节点。
有转移方程 。
void dfs(int u, int fa) {
dep[u] = dep[fa] + 1;
f[u][0] = fa; // 往上跳 1 个节点那就是父亲节点啦~
for (int i = 1; (1 << i) <= dep[u]; i++)
f[u][i] = f[ f[u][ i - 1 ] ][ i - 1 ];
for (auto v : G[u]) {
if (v == fa) continue;
dfs(v, u);
}
}
int LCA(int x, int y) {
if (dep[x] < dep[y]) swap(x, y);
for (int i = 20; i >= 0; i--) {
if (dep[ f[x][i] ] >= dep[y]) x = f[x][i];
if (x == y) return x;
}
for (int i = 20; i >= 0; i--)
if (f[x][i] != f[y][i]) x = f[x][i], y = f[y][i];
/*
这里为什么要写 if (f[x][i] != f[y][i]) x = f[x][i], y = f[y][i];
因为往上跳一个很大的距离最后节点编号肯定是相等的,
这样能够保证是公共祖先,但是不能保证是最近公共祖先,
所以应该始终保持两个节点的编号不相等,一直逼近最近公共祖先,
最终两个节点的父亲节点就是最近公共祖先。
*/
return f[x][0];
}
时间复杂度 。
3.3 Tarjan 算法
假如时间复杂度要求 呢?
这是一个值得深思的问题……
这里就不得不提到我们和蔼可亲的 Robert Tarjan 老爷爷了。
所以在线算法明显是不行了(其实通过四毛子可以做到在线),考虑离线。
假设有一棵优美的树:
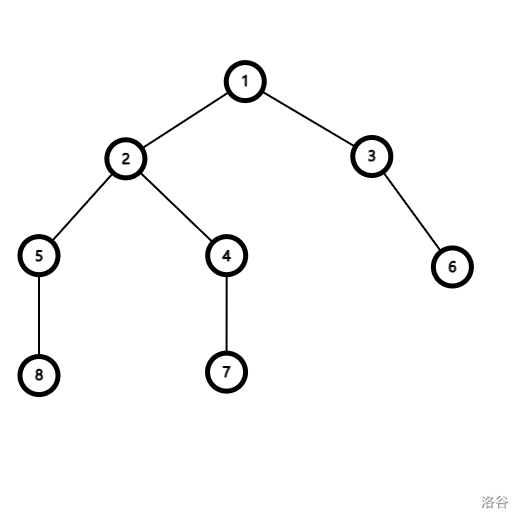
你需要求出 , 和 。
首先我们用 vector 把对应的查询挂到对应的节点上,例如:
struct query {
int x, id; // x 表示另一个节点,id 表示询问的编号
query() = default;
query(const int _x, const int _id) : x(_x), id(_id) {}
};
vector <query> q[N]; // 记录查询
int ans[N]; // 记录答案
q[5].push_back(query(4, 1));
q[4].push_back(query(5, 1));
// ...
然后我们用 Tarjan 算法(其实就是在 dfs 上搞点事情)。
这里求 LCA 我们需要用到并查集,这里给出常用的函数。
int f[N]; // 记录并查集中每一个节点的父亲节点编号
static inline
int find(int x) {
return (x ^ f[x] ? f[x] = find(f[x]) : x); // 路径压缩
}
先从 节点进入,然后遍历到 节点,但是 节点还没有被遍历过,所以不用管这个询问$。
遍历到 ,但是 没有被遍历过,所以不用管。
遍历到 节点,因为 已经被遍历过了,所以查询 函数,得到结果 。
由于 的子树内已经遍历完了,所以在并查集中从 向 的父亲 连边。
然后剩余的操作以次类推即可。
这里以 P3379 【模板】最近公共祖先(LCA) 为例放一下代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 5;
int n, m, s, f[N];
vector <int> G[N];
struct query {
int x, id;
query() = default;
query(const int _x, const int _id) : x(_x), id(_id) {}
};
vector <query> q[N];
int ans[N];
bool vis[N];
static inline
int find(int x) {
return (x ^ f[x] ? f[x] = find(f[x]) : x);
}
void merge(int x, int y) {
int fx = find(x), fy = find(y);
if (fx ^ fy) f[fx] = fy;
}
void Tarjan(int u, int fa) {
vis[u] = true;
for (auto v : q[u]) if (vis[ v.x ]) {
ans[ v.id ] = find(v.x);
}
for (auto v : G[u]) {
if (v == fa) continue;
Tarjan(v, u);
}
merge(u, fa);
}
int main() {
scanf("%d%d%d", &n, &m, &s);
for (int i = 1; i < n; i++) {
int u, v; scanf("%d%d", &u, &v);
G[u].push_back(v); G[v].push_back(u);
}
for (int i = 1; i <= n; i++) f[i] = i;
for (int i = 1; i <= m; i++) {
int x, y; scanf("%d%d", &x, &y);
q[x].push_back(query(y, i)); q[y].push_back(query(x, i));
}
Tarjan(s, s);
for (int i = 1; i <= m; i++) printf("%d\n", ans[i]);
return 0;
}
时间复杂度 ,使用树上线性并查集可以做到 ,虽然这并没有什么用(虽然是 的,但是跑的和 真心没区别)。
如果你正式理解了 Tarjan 求 LCA,那么 这道题 你就可以用 Kruskal 重构树 解决了。
4. 树上差分
例题:P3128 [USACO15DEC]Max Flow P
简要题意:
给出一棵 个节点的树,有 次修改操作,每次给定节点编号 和 ,把 到 的路径上的点权增加 ,问 次操作后最大点权的值。
对于 的数据,。
看到许多次修改操作,想到的肯定是差分。序列上的差分我就默认都会了,那么我们只需要把差分搬到树上就行了。
我们定义树上的前缀和就是
也就是前缀和指一棵子树内的所有权值之和。
我们考虑给 到 的路径上的所有点权 所带来的贡献。
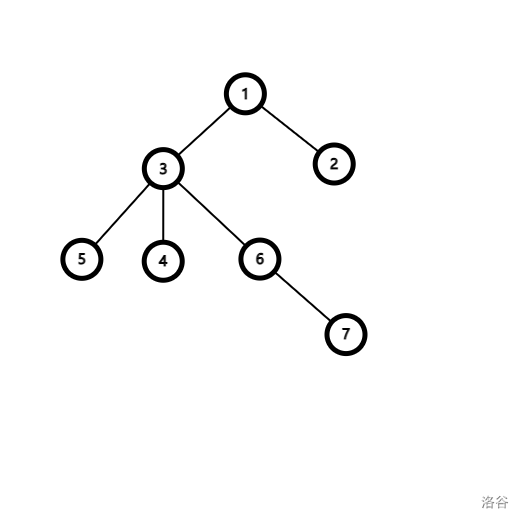
设 ,那么点 的点权都要 。
考虑差分怎么做,我们首先就要在 和 处 ,然后我们发现节点 满足条件了。
但是 ,也就是节点 处的点权却加了 ,这明显不符合,我们只要它加 就够了,所以我们就在 LCA 处减去 。
然后我们考虑 LCA 以上的部分,这里也就是节点 ,我们会发现这样节点 又加了 ,我们不希望节点 的权值和有变化,所以我们要在 LCA 的父亲节点处减去 。
这样树上差分就做好了。
int c[N], sum[N], ans(0);
void dfs(int u, int fa) { // 统计答案
sum[u] = 1;
for (auto v : G[u]) {
if (v == fa) continue;
dfs(v, u); sum[u] += sum[v];
}
ans = max(ans, sum[u]);
}
scanf("%d", &q);
while (q--) { // 树上差分
int s, t; scanf("%d%d", &s, &t);
int lca = LCA(s, t);
c[s]++; c[t]++; c[lca]--; c[ father[lca] ]--;
}
完结撒花!^_の



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 使用C#创建一个MCP客户端
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现