教堂第三次比赛出题

\(\texttt{T1 : Gold Experience Requiem}\)

出这道题的时候全国看 \(\texttt{JOJO}\) 的大概不到一千万....我现在已经退坑了..

因为是签到题,太水。

\[\texttt{25pts} \]

乱写?

\[\texttt{100pts} \]

1 -3 4 2 -1 7
求一波后缀和

然后把每一个后缀和与上一个后缀和比较大小 (如果没有上一个则与 \(0\))。

然后把后缀最大值求出来。

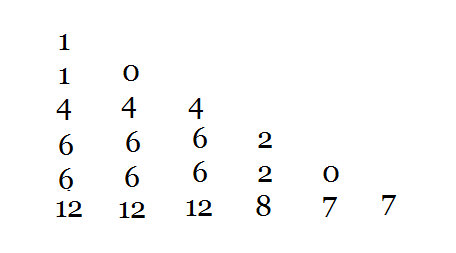
然后倒过来看一下。

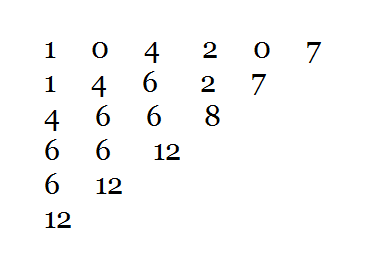
样例构图 :

暴力 \(N^2\) 即可,不过我还是卡了 \(N^2\) 空间。

$\texttt{T2 : Moment} $

\(\texttt{Zero-1}\) 作为中\(p\) 似乎已经非常优秀了呢...(怎么说你很懂术喽?)

\[\texttt{35 pts} \]

前缀和优化一下..

\[\texttt{100 pts} \]

这道题我本来想莫队的,突然发现贡献无法处理。

然后我在上政治课的时候 (为什么又是政治?) , 发现这个式子是可以差分的...

证明 ? 自己打一个暴力就知道了。

差分完以后我们发现要求的东西变成了这个 :

\[\sum\limits^{x}_{i=1} \sum\limits^{y}_{j=1}\ [num_i=num_j] \]

分块就可以了。我们记录每一个数字对每一个块的贡献,然后右边多出来的单点就可以放在桶里面乱搞。

$\texttt{T3 : No matter who will be the creator} $

这是生地中考前出的暴力可过大水题....

\[\texttt{30 pts} \]

先搞一搞这个区间的最大值,然后再用两层循环跑过去。

正所谓 \(N^3\) 过 \(10^3\)。

\[\texttt{60 pts} \]

首先我们想,这道题并没有修改,何不离线,可以想到莫队。考虑到逆序对,每一个点的贡献是 \(val_i\),\(num_i\) 在 \(i\)~\(r\) 的排名是 \(rank_i\),那么显然 \(val_i=num_i+num_j (l \leq i < j \leq r,rank_i=rank_j+1)\),这样子我们可以保证这个贡献最大,求出来后存在线段树里面即可。

考虑到 \(j\) 为存在于 \(i+1\)~\(r\),且刚好小于 \(num_i\) 的数,所以这就是一个求“前继”的过程,用某树求就可以了。时间复杂度均为 \(O(M \sqrt{N} \log N)\)。其实这个常数可以优化很多的,只需要一些骚操作,大概可以 \(\texttt{80 pts}\) 的样子...

\[\texttt{100 pts} \]

已经知道了 \(\texttt{60 pts}\) 的结论 \(\texttt{100 pts}\) 就很好推。

首先我们知道逆序对是这样定义的 : \(num_i>num_j , l \leq i < j \leq r\)

然后把贡献换一下 : \(num_j<num_i , l \leq i < j \leq r\)

也就是说,每一个贡献其实可以求它的前区间,而不是后区间。而且我们并不是求前区间的刚好比自己大的那个,如果要求这个贡献最优,那么一个点 \(j\) 的贡献绝对为 \(\max num_1\)~\(_{j-1}\)。

我们设一个序列 \(ans\{\}\),\(ans_i\) 为 \(1\)~\(i-1\) 的最大值。比如 1 8 5 4 2 5 6 3 的 \(ans\{\}\) 就为 0 0 8 8 8 8 8 8。我们把所有询问离线,按照 \(l\) 为第一关键字排序。\(i\) 从 \(1\)~\(n\) 遍历,然后我们看有没有询问的 \(l\) 为当前的 \(i\),如果有,则查询这些区间,查询这个区间 \(ans+num\) 的最大值。然后我们需要删除 \(i\) 这个数字对 \(ans\) 的贡献,出题人太菜所以并没有想出什么好办法,所以就用数据随机跑过去了 (如果用线段树的话有点悬,自测数据这个的运算次数大概有两三千万,加一个 \(log\) 可能就挂了)。
你会发现这个查询对 \(r\) 没有要求,所以按 \(l\) 排序就可以了。

其次这道题留下一个问题,一个序列 \(A\{\}\) 和一个序列 \(B\{\}\),\(B_i=\max A_1\)~\(_{i-1}\),支持区间查询 \(l\)~\(r\) 的 \(\max A_i+B_i\),支持从前到后逐次删除 \(A_i\) 并且维护 \(B_i\) 的正确性。

希望有大佬碾爆这个题解。