CDQ分治 从逆序对到三维偏序

使用\(CDQ\)实现偏序问题

\(CDQ\) 分治本身很好理解,只是复杂度有点玄学而已。

逆序对问题

贡献定义为 \(j=1...i-1\) 中求出 \(a[j]>a[i]\)。这样子朴素的算法就很简单,只需要对 \(1...i-1\) 进行遍历,时间复杂度 \(O(n^2)\)。不过也有 \(O(n\ log\ n)\) 的方法,这里做下铺垫,先讲解权值线段树的做法。

每加入一个数字,我们可以把这个数字插入到权值线段树中,如下:

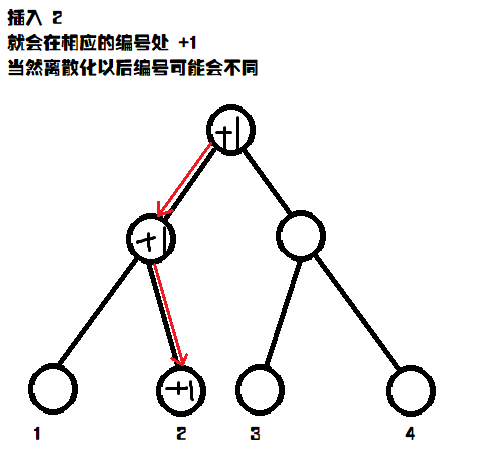
当到第 \(i\) 个数字的时候,我们就可以直接在权值线段树中查询 \(num[i]...max\) (其中 \(max\) 为 \(1...i-1\) 最大的值)。这就是第 \(i\) 个数的贡献。查询完以后记得要继续插入此数。

权值线段树转化为树状数组

这就比较好理解,跟权值线段树大同小异,查询、修改都差不多(甚至是参数也相同)。

偏序问题的定义

什么是偏序? \(N\) 维偏序,也就是给你 \(N\) 个数组,\(i\)的贡献定义为数组 \(1\) 数组 \(2.....\) 数组 \(N\) 的第 \(i\) 个数在这 \(N\) 个数组中满足 数组 \(1[i]\)
\(2[i] .... N[i] \leq 1[j],2[j]....N[j]\)。(\(1\leq i,j\leq N\))

或许有点模糊,我们用二维偏序来说。给定数组 \(a,b\)。如果 \(a[j]\leq a[i]\) 且 \(b[j]\leq b[i]\) 的话,就算是一个贡献。\(N\) 维也是如此。

如何解决问题

其实都可以用权值线段树或者树状数组来完成此类问题,这里来讲一下 \(CDQ\) 分治。 \(CDQ\) 分治和其它数据结构差不多,几乎都是每多一维,时间复杂度多个 \(log\ n\)。那么二维偏序直接用树状数组,这里不多说。

\(CDQ\) 大体可以认为是 先算出 \(l\)~\(mid\) 的贡献,然后算出 \(l\)对\(r\) 的贡献,最后再算 \(mid\)~\(r\) 的贡献。对于 \(l\)~\(mid\) 和 \(mid\)~\(r\) 的贡献,可以直接 \(CDQ(l,mid),CDQ(r,mid)\)。为什么呢?因为分治以后它们会对自己的 \(l\)~\(r\) 算自己的贡献,所以这样子木有问题。现在讨论的重点就是如何求出 \(l\)~\(r\) 的贡献。

三维偏序问题: 偏序问题的第一维,我们是直接排序的。注意要按第 \(1\) 个数组为第 \(1\) 关键字,第 \(2\) 个为第 \(2\) 个关键字 \(.....\)。然后我们就可以保证整个数组 \(a[i]\leq a[j]\ (i\leq j)\)。我们现在有一个区间 \(l,r\) ,我们先 \(CDQ(l,mid)\)。随后我们给 \(l,r\) 这个区间进行编号, \(num[i]:=i\)(这个时候 \(num\) 为编号)。我们再用一个数组 \(element[l\)~\(r]\) 为 \(l\)~\(r\) 的 \(b[i]\),然后进行 \(Sort(l,r)\)。其中 \(element\) 为第一关键字, \(num\) 为第二关键字。

最后循环扫一遍,因为这个时候后已经满足 \(b[i]\leq b[j]\ (i\leq j)\)。我们就可以按照逆序对这样子,对权值线段树(树状数组)插入第三维 \(c[i]\)。如果 \(num[i]\leq mid\) 的话,我们就插入,否则算贡献。为什么这样子呢?因为现在满足的是 \(b[i]\leq b[j]\ (i\leq j)\) ,而 \(num[i]\leq mid\) 可以满足 \(a[l\)~\(mid]\leq a[mid+1\)~\(r]\),我们只需要对 \(c\) 数组进行逆序对一样的操作。

procedure CDQ(l,r:longint);
var
    mid,i,j:longint;
begin
    if l=r then exit; //到了叶子,退出
    mid:=(l+r) div 2;
    CDQ(l,mid); //先左边

    for i:=l to r do //赋值
    begin
        element[i]:=point[2,i]; //第二维
        num[i]:=i; //编号
    end;
    Sort_2(l,r); //进行排序,关键字如上述

    for i:=l to r do
        if num[i]<=mid then //左边的,插入
            Insert(point[3,num[i]],1)
        else
            inc(value[num[i]],Query(point[3,num[i]])); //算贡献
    for i:=l to r do //还原树状数组
        if num[i]<=mid then
            Insert(point[3,num[i]],-1); //还原,所以是-1
    CDQ(mid+1,r); //再往右边
end;

\(a[l\)~\(mid]\leq a[mid+1\)~\(r]\) 是只能算出 \(l\) 对 \(r\) 的贡献的,所以就需要分治啦。最后别忘了还原树状数组和 \(CDQ(mid+1,r)\)!!! 加上树状数组时间复杂度 \(O(n\ (log\ n)^2)\)。

三维偏序就如此,谢谢大家。