FFT 11个问题速成

网上的博客讲的挺不错 , 只是有一些意义没有提到。
使得人很容易搞混淆 , 记不住。
以下 \(n\) 默认为 \(2^z\)。

\(\text{Q1}\) : \(\text{FFT}\) 用处是 ?

\(\text{FFT}\) 的用处就是在 \(O(n \log n)\) 的时间内求出两个多项式的卷积。
简单点说 , 多项式就是解析式 , \(\text F(x)=\sum\limits^{n-1}_{i=0} a_ix^i\) 。
卷积就是两个多项式相乘 , \(\text{A(x)}=\sum\limits^{n-1}_{i=0} a_ix^i\) , \(\text{B(x)}=\sum\limits^{n-1}_{i=0} b_ix^i\) , 那么
\(\text C(x)=\text A(x) *\text B(x) = \sum\limits^{n-1}_{i=1}\sum\limits^{n-1}_{j=1} a_ib_jx^{i+j}=\sum\limits^{n-1}_{i=1} c_i\) , 其实按照 \(x\) 的次数排序即可。
一般来说这样子的时间复杂度是 \(O(n^2)\) 的。

\(\text{Q2}\) : \(\text{FFT}\) 的基本流程是 ?

\(\text{FFT}\) 的基本流程是 : 系数表达式 \(\xrightarrow[O(n \log n)] {\text{DFT}}\) 点值表达式 \(\xrightarrow[O(n)] {\text{相乘}}\) \(\text A*\text B\) 的点值表达式 \(\xrightarrow[O(n \log n)] {\text{IDFT}}\)\(\text A*\text B\) 的系数表达式 , 得出答案。
是不是很简单呢。

\(\text{Q3}\) : 什么是点值表达式 ?

很简单 , 想象一次函数 , 是不是可以通过两个点求出来解析式。
结论 : \(n\) 次多项式 , 只需要 \(n+1\) 个点来确定。
我们可以这样表示 \(\text X=\{(x_0,\text F(x_0)),(x_1,\text F(x_1)) \dots (x_n,\text F(x_n))\}\)。

\(\text{Q4}\) : 为什么要转化成点值表达式 ?

当两个多项式变成点值表达式后 , 它们可以直接相乘 , 再换成系数表达式。
比如 , \(\text A*\text B=\text C\) , 那么 :
\(\text X_{\text A*\text B}=\{(x_0,\text F_{\text A}(x_0)\text F_{\text B}(x_0)),(x_1,\text F_{\text A}(x_1)\text F_{\text B}(x_1)) \dots (x_n,\text F_{\text A}(x_1)\text F_{\text B}(x_1))\}\) 其实就是
\(\text X_{\text C}=\{(x_0,\text F_{\text C}(x_0)),(x_1,\text F_{\text C}(x_1) \dots (x_n,\text F_{\text C}(x_n)\}\)。
这亚子的时间复杂度是 \(O(n)\) 的没错。

\(\text{Q5}\) : 为什么要学习复数和单位根 ? 什么是复数 ?

总的来说 , 单位根是 \(\text{FFT}\) 快速转换的原因 , 但因为单位根涉及复数所以要提及。
复数 , 就是形为 \(a+bi\) 的数字 , 其中 \(i=\sqrt{-1}\)。显然 \(a\) 为实部 \(b\) 为虚部。
对于普通的加减乘除 , 把 \(i\) 看作一个字母 , 运算完以后分出实虚部即可。
一个复数的共轭 , 就是 \(a-bi\) , 因为要满足此复数乘共轭为实数。
很显然 \((a+bi)(a-bi)=a^2+b^2\)。
一个复数的除法只需要乘分母的共轭即可 , 如 \(\frac{a+bi}{c+di}=\frac{(a+bi)(c-di)}{(c+di)(c-di)}=\frac{ac+bd}{c^2+d^2}+\frac{bc-ad}{c^2+d^2}i\)。

\(\text{Q6}\) : 复数的函数图像是怎样的 , 进行运算以后会变成怎样 ?

\(y\) 轴不再是你熟悉的标整数了 , 标的是 \(yi\) , 如下图。
假如我们有点 \((1,2i)\) 和 \((2+2i)\) , 它们相乘以后变为 \(-2+6i\) , 那么在坐标轴中会有一些相关的性质。
红色的长为模长 , 它的值为 \(\sqrt{a^2+b^2}\)。蓝色的叫幅角。

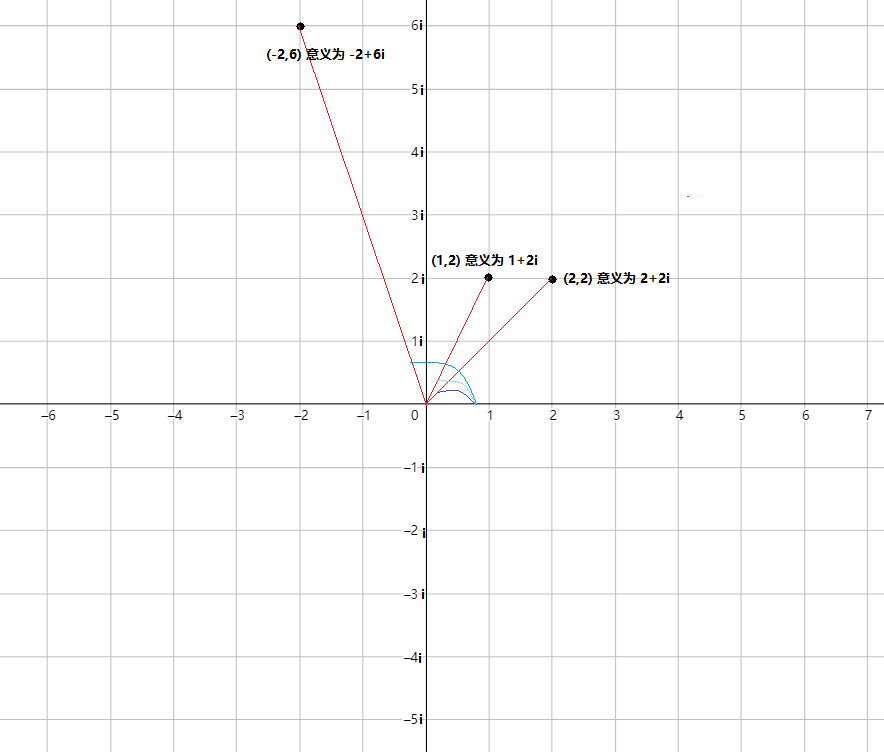
可以看出 , 乘法做完后 , 模长先乘 , 幅长相加。

\(\text{Q7}\) : 单位根是什么 ?

简单来说单位根是一堆复数 , 标记为 \(\omega_n^k\) , omega。
它表示下来的值是 \(a+bi\) , 不是 \(bi\) , 也不是 \(b\) , 不要误认。
是怎样一些复数呢 ?
它们要满足一个性质 , 就是模长为 \(1\)。也就是 \(\sqrt{a+b}=1\)。
那不是一个圆吗 ?
是的。

那为什么还有 \(n\) 和 \(k\) 这种东西 ?
其实 ， 它的真正定义 , 是把圆 \(n\) 等分以后 , 第 \(k\) 个等分的点表示的值。从 \(0\)~\(n-1\) 的 \(n\) 个点哦。

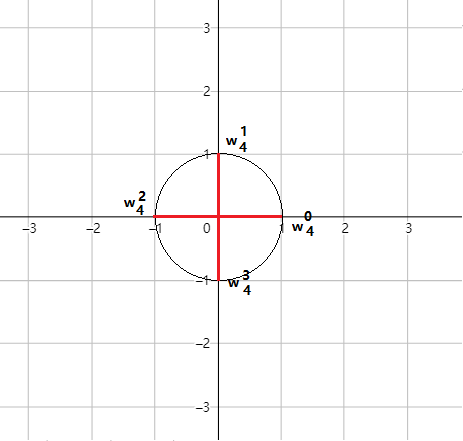
很显然的是 , \(\omega^2_4=-1 , \omega^0_4=i\) 。
它们有一个很显然的公式 : (\(\pi\) 是平角度数 , 复读机)

\[\omega^k_n=\cos \frac k n 2\pi+i\sin \frac k n 2\pi \]

其中我们可以发现 \(\frac {k360°} n\) 是幅角。
这个公式为什么成立 ? 其实很简单 , 我们的斜边也就是模长都是 \(1\) , 那么我们只要直角边就可以了。

\(\text{Q8}\) : 单位根有什么性质 ?

根据公式 , \(\omega\) 的大小你可以看作也是幅角。
有些时候 , 你可以把 \(\omega^k_n\) 看作 \(w^{\frac k n}\)。 (玄学)

• 性质 \(\text I\) : \(\omega^a_n \times \omega^b_n=\omega^{a+b}_n\)。
  • 子性质 : \((\omega^1_n)^k=\prod^k_{i=1}=\omega^k_n\)
• 性质 \(\text{II}\) : \(\omega^{k \mod n}_n=\omega^k_n\) , 过于显然。
• 性质 \(\text{III}\) : \(\omega^{ak}_{an}=\omega^k_n\) 。 总编号多一倍 , 你自己的编号也多一倍 , 这个比是不会变的 , 幅角不变。
• 性质 \(\text{IV}\) : \(\omega^{k+\frac n 2}_n=-\omega^k_n [n \mod 2=0]\) , 轴对称过去 , 显然。

\(\text{Q9}\) : 如何将单位根应用到 \(\text{DFT}\) 里面 ?

很简单的。
假设你现在有一个普通的多项式 \(\text F(x)=\sum\limits^{n-1}_{i=0} a_ix^i\)。
那么我们再设 \(\text F_1(x)=\sum\limits^{\frac n 2-1}_{i=0} a_{2i}x^i\) , \(\text F_2(x)=\sum\limits^{\frac n 2-1}_{i=0} a_{2i+1}x^i\)。
什么意思 ? 就是把系数拍成两半 , 一边是偶数系数 , 一边是奇数系数。
而 \(x\) 的次数不会变 , 且次数到 \(\frac n 2-1\) 就停了。

我们可以得到关系式 , \(\text F(x)=\text F_1(x^2)+x\text F_2(x^2)\)。
这个关系式极为重要。
我们随便代几个单位根进去 , 首先是 \(\omega^k_n\) :

\[\begin{aligned} \text F(x)= & \text F_1(x^2)+x\text F_2(x^2) \\ \text F(\omega^k_n)= & \text F_1(\omega^{2k}_n)+\omega^k_n\text F_2(\omega^{2k}_n) \\ \text F(\omega^{k}_n)= & \text F_1(\omega^{k}_{\frac n2})+\omega^k_n\text F_2(\omega^k_{\frac n 2}) \\ \end{aligned}\]

我们会发现 \(\omega^k_n\) 可以用值求出来 , 其它的递归即可。
但是这样子只到 $\frac n 2 $ 啊 , 注意到 \(k < \frac n 2\)。
我们再套一个 \(-\omega^k_n\)。

\[\begin{aligned} \text F(x)= & \text F_1(x^2)+x\text F_2(x^2) \\ \text F(-\omega^k_n)= & \text F_1(\omega^{2k}_n)-\omega^k_n\text F_2(\omega^{2k}_n) \\ \text F(\omega^{k+\frac n 2}_n)= & \text F_1(\omega^{k}_{\frac n2})-\omega^k_n\text F_2(\omega^k_{\frac n 2}) \\ \end{aligned}\]

在 \(k < \frac n 2\) 的情况下我们也可以递归了。
注意到指数级减少 , \(O(n \log n)\) 的复杂度啦。

\(\text{Q10}\) : \(\text{IDFT}\) 如何操作 ?

结论 : 将所有求出来的 \(\text F(\omega^k_n)^{-1}\) 变为一个新的多项式的系数 , 再做一遍 \(\text{DFT}\) , 所有系数再除个 \(n\) , 即可得出每一个系数。
玄学 ?

\(\text{Q11}\) : \(\text{IDFT}\) 的操作怎样证明 ?

都是口胡 , 感谢 \(\text{alpha1022}\) 大佬的帮助。
下面引用大佬的话。
这其实是一个解线性方程的问题 , 给出了 \(n\) 个线性方程。

\[\begin{bmatrix} a_0(\omega^0_n)^0 +a_1(\omega^0_n)^1 \dots+a_{n-1}(\omega^0_n)^{n-1} & = \ \text F(\omega^0_n) \\ a_0(\omega^1_n)^0+a_1(\omega^1_n)^1 \dots+a_{n-1}(\omega^1_n)^{n-1} & = \ \text F (\omega^1_n) \\ \vdots \\ a_0(\omega^{n-1}_n)^0+a_1(\omega^{n-1}_n)^1 \dots+a_{n-1}(\omega^{n-1}_n)^{n-1} & = \ \text F(\omega^{n-1}_n) \\ \end{bmatrix}\]

其实也就是 :

\[\begin{bmatrix} (\omega^0_n)^0 &(\omega^0_n)^1 \dots &(\omega^0_n)^{n-1} \\ (\omega^1_n)^0 &(\omega^1_n)^1 \dots &(\omega^1_n)^{n-1} \\ & \vdots \\ (\omega^{n-1}_n)^0 &(\omega^{n-1}_n)^1 \dots &(\omega^{n-1}_n)^{n-1} \\ \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ \vdots \\ a_{n-1} \\ \end{bmatrix} = \begin{bmatrix} \text F(\omega^0_n) \\ \text F(\omega^1_n) \\ \vdots \\ \text F(\omega^{n-1}_n) \\ \end{bmatrix} \]

我们记录最左边这个矩阵为 \(\text E\) , 那么再来一个 \(\text{D}\) , 设 \(\text V=\text {ED}\) :

\[\text D=\begin{bmatrix} (\omega^0_n)^0 &(\omega^0_n)^1 \dots &(\omega^0_n)^{n-1} \\ (\omega^{-1}_n)^0 &(\omega^{-1}_n)^1 \dots &(\omega^{-1}_n)^{n-1} \\ & \vdots \\ (\omega^{1-n}_n)^0 &(\omega^{1-n}_n)^1 \dots &(\omega^{1-n}_n)^{n-1} \\ \end{bmatrix}\]

也就是 \(\text E\) 的逆矩阵。证明 :

当 \(i=j\) 时 , \(v_{i,j}=n\)。
当 \(i \not =j\) 时 ，

\[\begin{aligned} v_{i,j}= &\sum\limits^{n-1}_{k=1} (\omega^{j-i}_n)^k \\ = & \frac{1-(\omega^{j-i}_n)^n}{1-(\omega^{j-i}_n)} \\ = & 0 \\ \end{aligned}\]

我们要求的是中间的矩阵 , 又知道右边的 , 就拿右边的乘上 \(\text D\) 即可。而且这个逆矩阵少出来贡献为 \(n\)>
即 :

\[\begin{bmatrix} (\omega^0_n)^0 &(\omega^0_n)^1 \dots &(\omega^0_n)^{n-1} \\ (\omega^{-1}_n)^0 &(\omega^{-1}_n)^1 \dots &(\omega^{-1}_n)^{n-1} \\ & \vdots \\ (\omega^{1-n}_n)^0 &(\omega^{1-n}_n)^1 \dots &(\omega^{1-n}_n)^{n-1} \\ \end{bmatrix} \begin{bmatrix} \text F(\omega^0_n) \\ \text F(\omega^1_n) \\ \vdots \\ \text F(\omega^{n-1}_n) \\ \end{bmatrix} \times n = \begin{bmatrix} a_0 \\ a_1 \\ \vdots \\ a_{n-1} \\ \end{bmatrix} \]