P4197 【Peaks】克鲁斯卡尔重构树详解
\(\texttt{Kruskal}\) 重构树 —— 需要一定基础的简单算法
题目大意:
- 给你一个无向图,可能有很多个连通块
- 给定一些询问 \(v,x,k\),代表在 \(v\{\}\) 这个连通块里面找到一些路径
\(v \Longrightarrow u\{\}\) 的边权 \(max\{val\{\}\} \leq x\)。求 \(u_k\)。
首先我们思考,我们要满足最小的边权,那么是整个图的最小生成树的点,而不是 \(v \Longrightarrow u\) 的最短路径 (有可能最大值会大,但是总值小)。因为最小生成树互相连的都是最小的边。
举个很简单的例子 :
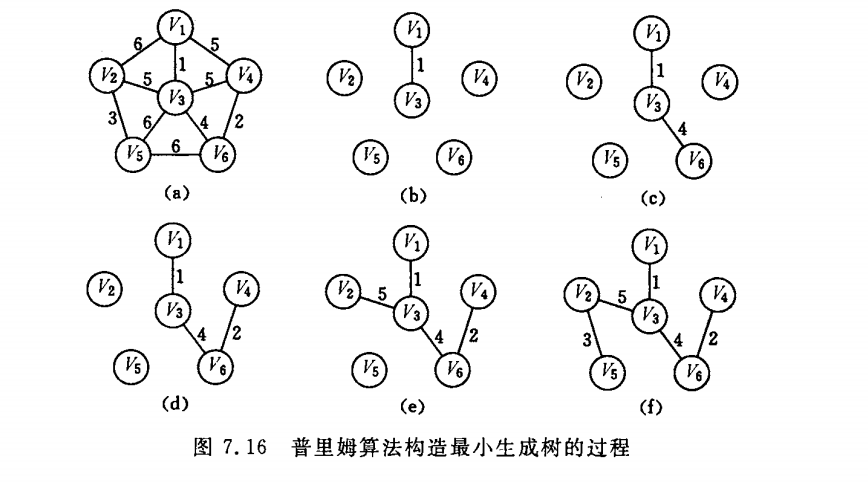
\(V_3 \Longrightarrow V_4\) 的最短路应该是 \(V_3 \Longrightarrow V_4\),距离为 \(5\),最大值为 \(5\)。而最小生成树以后,\(V_3 \Longrightarrow V_4\) 的路是 \(V_3 \Longrightarrow V_6 \Longrightarrow V_4\),距离为 \(6\),最大值为 \(4\)。
然后我们知道,最小生成树了以后就变成了一棵树,然后可以再这上面做文章。如果我们表示一种东西,它的存在满足所有路径通过自己的时候,自己的值为这条道路的最大值,并且满足一定的点在某一个地方,一定的点在另一个地方,每一个点要经过一些必须点来通过。
所以有一种东西叫 \(\texttt{Kruskal}\) 重构树。
首先我们先把边排好,然后开始一条一条重构。
假如我们有一个图 :
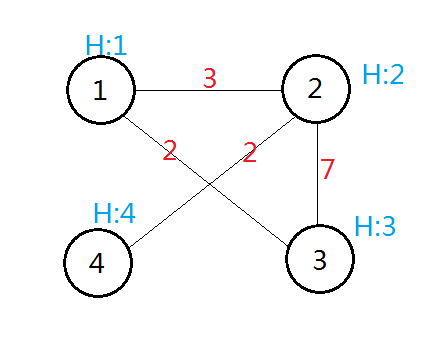
那么我们先按边最小的 \(1 \Longrightarrow 2\) 开始。
我们新建一个节点,编号随便,权值为 \(val\{1 \Longrightarrow 3\}\),也就是 \(2\)。
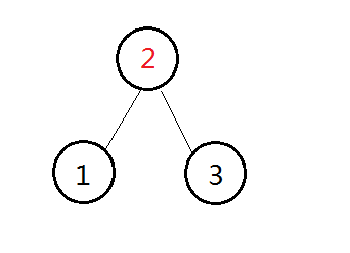
然后是 \(2 \Longrightarrow 4\)
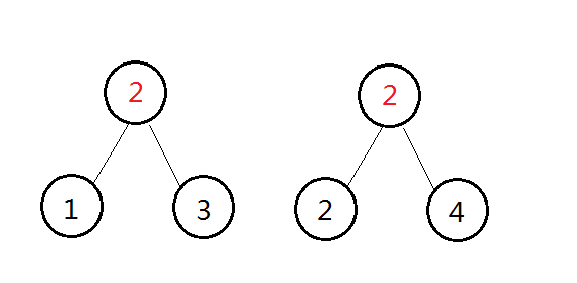
做到 \(1 \Longrightarrow 2\) 时候我们发现 \(1\) 和 \(2\) 各自已经有父亲,或者说各自形成了各自的树,现在是一个森林局面。然后我们把各自的根相连,权值为 \(\{1,3\} \Longrightarrow \{2,4\}\),也就是 \(1 \Longrightarrow 2\),为 \(3\)。
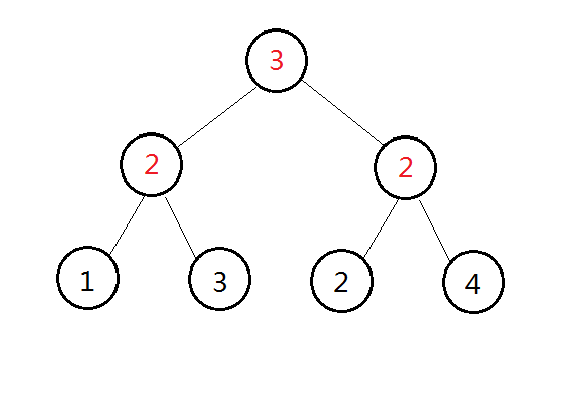
然后最后一条边为 \(2 \Longrightarrow 3\),我们发现这两个点已经在同一个树,就不用管它们了。
以上是重构过程,我们来看一下其性质。首先一个非叶子节点 \(u\) 代表自己的子树的叶子节点到达 \(u\) 的路径的最小权值为 \(u\),且其所包含的叶子节点绝对在同一个连通块。其次,这棵树一定是一个二叉堆,二叉是因为每一次是两两结合,最大堆是因为从小到大排序后依次合并。
这时候我们就可以知道,如果我们从 \(v\) 这个点一直往上跑,然后找到一个点 \(p\),满足 \(val_p \leq k\) 且 \(val_{father_{p}} > key\) 的时候,这棵树的叶子节点就可以表示所有的 \(v\) 能到达的图中的点。
好了,以上暴力。
我们考虑到一个性质,这是一个二叉堆,但不是完全二叉树,所以高度不一定是 \(O(\log N)\) 的,有可能会卡到 \(O(N)\)。(高度会被卡成是 \(\frac{N}{2}-1\))
所以我们用到树剖。
我们假设有这样一个重构树,然后按照轻重链剖分搞出来。
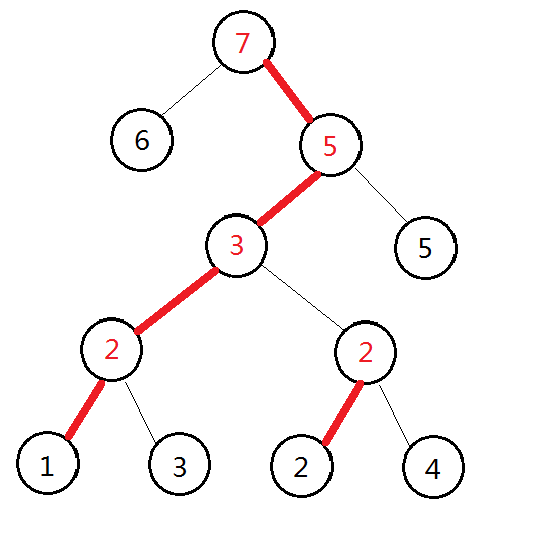
假如我们求从 \(4\) 往上找,一直找到 \(u\) 满足 \(val_u \leq 5\)。那么显然 \(5\) 是 \(7\) 的右二子。 (这两个点我讲得是权值不是编号)
我们到 \(4\) 的父亲,然后找这条链的最大值,发现是 \(2\) ,继续往上跳,跳到 \(3\),这个链的最大值是 \(7\),然后我们就二分,找到这个点就好了。
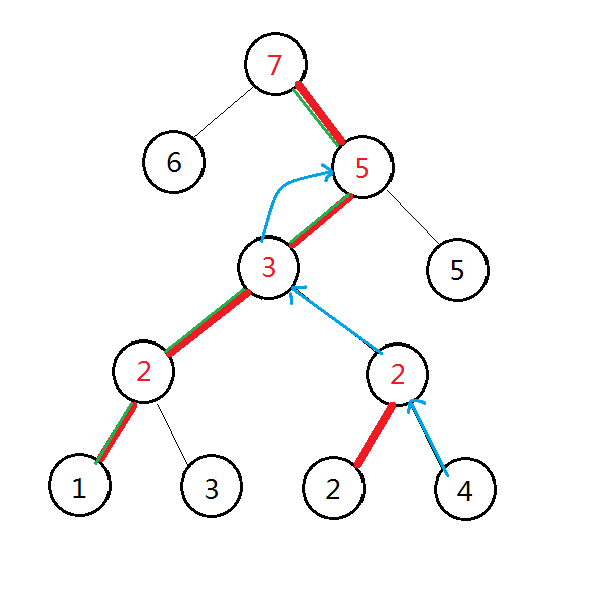
最后我们只需要求非叶子节点的子树中的叶子节点的最左边的编号和最右边的编号,求这些点的高度的第 \(k\) 大,这个编号为 \(\texttt{Dfs}\) 到的顺序。这个图可能有很多个连通块,你的 \(dfn\) 一直增加也是没有问题的。
求第 \(k\) 大? 划分树。
Uses math;
Const
total=100010 << 1; // 点数
edge=400010 << 1; // 边数
var
dsu,num,val,dfn,dep,top,size,recf,father:array[-1..total] of longint;
tree,toleft:array[-1..21,-1..total] of longint;
son,element:array[-1..total,-1..2] of longint;
input:array[-1..edge,-1..3] of longint;
i,n,m,x,y,k,sa,hop,test,tail,root,dfnum:longint;
function Get(x:longint):longint; // 并查集
begin
if dsu[x]=x then exit(x) else begin Get:=Get(dsu[x]); dsu[x]:=Get; end;
end;
procedure Sort(l,r:longint); // 排序
var i,j,s:longint;
begin
i:=l; j:=r; s:=input[(l+r) >> 1,3];
repeat
while (input[i,3]<s) do inc(i);
while (input[j,3]>s) do dec(j);
if i<=j then
begin
input[0]:=input[i]; input[i]:=input[j]; input[j]:=input[0];
inc(i); dec(j);
end;
until i>=j;
if i<r then Sort(i,r);
if j>l then Sort(l,j);
end;
procedure Dfs_1(x:longint); // 轻重链剖分
var i:longint;
begin
size[x]:=1;
for i:=1 to 2 do
if (dep[son[x,i]]=0)and(son[x,i]<>0) then
begin
dep[son[x,i]]:=dep[x]+1;
father[son[x,i]]:=x;
Dfs_1(son[x,i]); inc(size[x],size[son[x,i]]);
if size[son[x,i]]>size[son[x,0]] then son[x,0]:=son[x,i];
end;
end;
procedure Dfs_2(x,centre:longint); // 同样是树剖
var i:longint;
begin
inc(dfnum); dfn[x]:=dfnum; recf[dfnum]:=x; top[x]:=centre;
if son[x,0]=0 then
begin
inc(tail); val[tail]:=num[x];
element[x,1]:=tail; element[x,2]:=tail; exit; // element[x,0/1] 是这个点的编号
end;
Dfs_2(son[x,0],centre);
for i:=1 to 2 do if (son[x,i]<>son[x,0]) then Dfs_2(son[x,i],son[x,i]);
element[x,1]:=min(element[son[x,1],1],element[son[x,2],1]); // 叶子节点最大编号
element[x,2]:=max(element[son[x,1],2],element[son[x,2],2]); // 叶子节点最小编号,这两个在一起用来指导第 k 大的范围
end;
function Refer(x,key:longint):longint; // 查询 u 点的所在位置
var l,r,mid,tmp:longint;
begin
x:=father[x];
while (x<>root) do
begin
if num[top[x]]>key then break; // 如果这条链的最大值 > x
x:=top[x];
if num[father[x]]<=key then x:=father[x] else break; // 如果下一条链有 u (如果下一条链合法)
end;
l:=1; r:=dep[x]-dep[top[x]]+1; // 二分,因为一条链的 dfn 在一起
while l<=r do
begin
mid:=(l+r) >> 1; tmp:=recf[dfn[x]-mid+1];
if num[tmp]<=key then begin l:=mid+1; Refer:=tmp; end else r:=mid-1;
end;
end;
procedure Build(left,right,deep:longint); // 划分树预警
var i,mid,same,ls,rs,flag:longint;
begin
if left=right then exit;
mid:=(left+right) >> 1; same:=mid-left+1;
for i:=left to right do if tree[deep,i]<val[mid] then dec(same);
ls:=left; rs:=mid+1;
for i:=left to right do
begin
flag:=0;
if (tree[deep,i]<val[mid])or((tree[deep,i]=val[mid])and(same>0)) then
begin
flag:=1; tree[deep+1,ls]:=tree[deep,i]; inc(ls);
if tree[deep,i]=val[mid] then dec(same);
end else begin tree[deep+1,rs]:=tree[deep,i]; inc(rs); end;
toleft[deep,i]:=toleft[deep,i-1]+flag;
end;
Build(left,mid,deep+1); Build(mid+1,right,deep+1);
end;
function Query(left,right,k,l,r,deep:longint):longint;
var mid,x,y,cnt,rx,ry:longint;
begin
if left=right then exit(tree[deep,left]);
mid:=(l+r) >> 1;
x:=toleft[deep,left-1]-toleft[deep,l-1];
y:=toleft[deep,right]-toleft[deep,l-1];
ry:=right-l-y; rx:=left-l-x; cnt:=y-x;
if cnt>=k then Query:=Query(l+x,l+y-1,k,l,mid,deep+1)
else Query:=Query(mid+rx+1,mid+ry+1,k-cnt,mid+1,r,deep+1);
end;
begin
read(n,m,test);
for i:=1 to n do read(num[i]);
for i:=1 to n << 1 do dsu[i]:=i;
for i:=1 to m do read(input[i,1],input[i,2],input[i,3]);
Sort(1,m);
for i:=1 to m do // 建立重构树
begin
x:=input[i,1]; y:=input[i,2]; dsu[x]:=get(x); dsu[y]:=get(y);
if dsu[x]=dsu[y] then continue;
inc(n); num[n]:=input[i,3]; son[n,1]:=Get(x); son[n,2]:=Get(y);
dsu[Get(x)]:=dsu[n]; dsu[Get(y)]:=dsu[n];
end;
for i:=1 to n do // 做树剖操作
begin
if father[i]<>0 then continue; root:=Get(i);
dep[root]:=1; father[root]:=root; Dfs_1(root); Dfs_2(root,root);
end;
for i:=1 to tail do begin tree[0,i]:=val[i]; input[i,3]:=val[i]; end;
Sort(1,tail);
for i:=1 to tail do val[i]:=input[i,3];
Build(1,tail,0);
for i:=1 to test do
begin
read(x,y,k); hop:=Refer(x,y); sa:=element[hop,2]-element[hop,1]+1;
if sa<k then begin writeln(-1); continue; end;
writeln(Query(element[hop,1],element[hop,2],sa-k+1,1,tail,0));
end;
end.
时间复杂度为 \(O(M \log N)\),查询点 \(u\) 每一次用 \(2\) 个 \(\log\),划分树用 \(1\) 个 \(\log\)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号