梯度下降法求函数最小值 基于matlab实现

算法原理

梯度下降法是一个最优化算法，可以用来求一个函数的最小值，最大值等，也常用于人工神经网络中更新各个感知器之间的权值，求出cost function的最小值等，应用广泛。
其原理简单，就求函数的最小值这个应用而言，大致说来就是先求出该函数梯度，大家都知道梯度是一个函数在该点的最快上升率，那么求个相反数就是最快下降率了。将每个自变量按下列公式更新：

xt+1=xt+Δx

其中

Δx=−η∂f∂x

η称为学习速率，也称为步长，指明了自变量朝向最快下降方向减少的速度，这个值的选定相当重要，太大了会导致震荡，无法收敛到最小值点，太小了会导致收敛速度过慢。
当xt+1和xt的差小于一个阀值时，就可以停止循环了。

Matlab实现

% 没有加入冲量项的随机梯度下降法实现
syms x y real
y(x) = x^2+2*x+10 ;
delta(x) = -diff(y(x)) ;
step = 0.1 ;
first_x = 10 ;
x_current = first_x ;
x_next = first_x ;
show_tmp = 0 ;
show = [] ;
counter = 0 ;
delta_last = 0 ;
while (true)
    delta_x = double(delta(x_current))*step ;
    if(abs(delta_x) < 0.0001)
        break
    end
    x_next = x_current + delta_x ;
    x_current = x_next ;
    counter = counter + 1;
    show_tmp = x_next ;
    show = [show, show_tmp] ;
    if(counter > 200)
        break ;
    end
end
x_next
counter
figure(1)
ezplot(y(x))
hold on 
plot([-100, 100],[double(y(x_next)), double(y(x_next))],'-r')
double(y(x_next))
figure(2)
plot(show)
pause
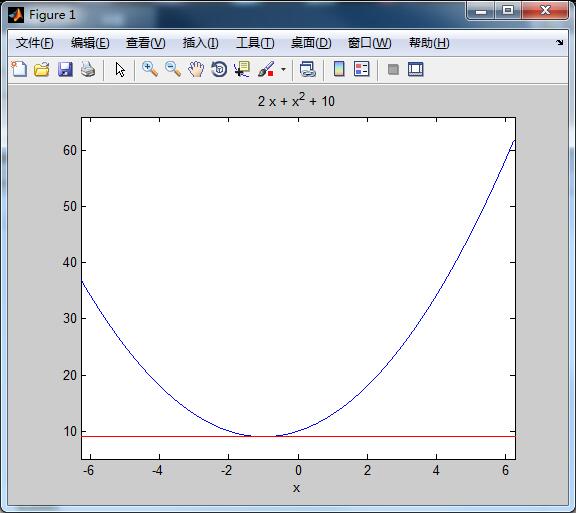
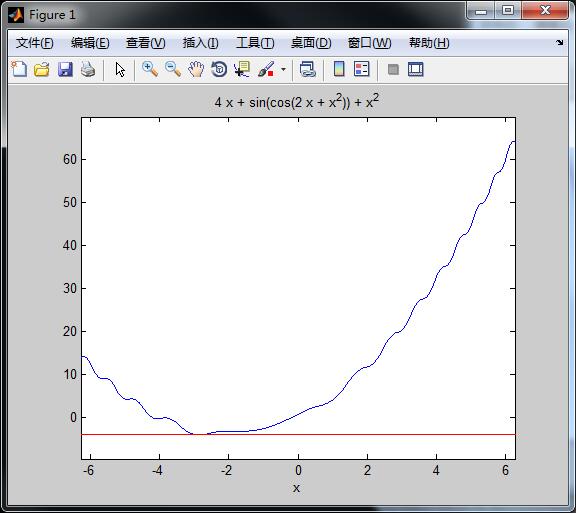
close all

待求解的函数曲线图像如下所示，其中的红线为梯度下降法算出来的最小值，可以看出来梯度下降法成功求出了该函数的最小值。

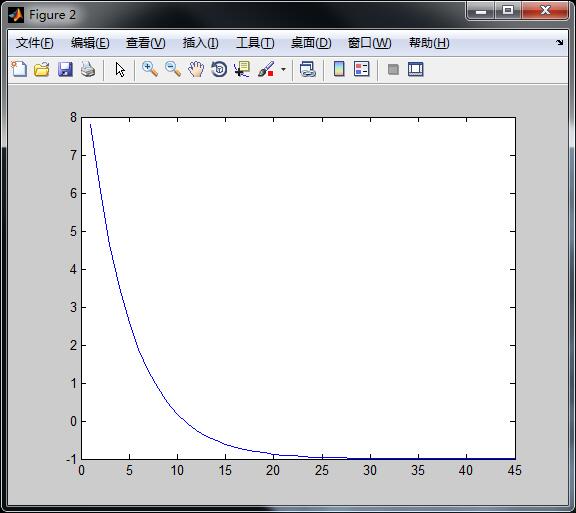
自变量的变化曲线，可以看出当循环超过25次时，此时的x已经很接近最小值点了，收敛速度取决于步长step。

各位可以自行调整步长和初始值，观察其收敛速度的变化，需要注意的是，这个步长如果太大将会导致震荡，无法收敛到最小值点，如果太小，将导致收敛速度太慢。
——————————————————————————————
另外，这个函数因为是二次函数，没有多个极点，因此梯度下降法能够在不陷入局部最优的情况下找到最大值，如果是存在多个极点的复杂函数会怎么样呢？让我们看下以下例子：

% 加入了冲量项，缓解陷入局部最优的随机梯度下降算法
syms x y real
y(x) = x^2+4*x+sin(cos(2*x+x^2)) ;
delta(x) = -diff(y(x)) ;
step = 0.1 ;
first_x = 10 ;
x_current = first_x ;
x_next = first_x ;
show_tmp = 0 ;
show = [] ;
counter = 0 ;
delta_last = 0 ;
alpha = 0; % 冲量项比例系数，设为0相当于没有加入冲量项
while (true)
    delta_x = double(delta(x_current))*step + delta_last*alpha;
    delta_last = delta_x ;
    if(abs(delta_x) < 0.0001)
        break
    end
    x_next = x_current + delta_x ;
    x_current = x_next ;
    counter = counter + 1;
    show_tmp = x_next ;
    show = [show, show_tmp] ;
    if(counter > 200)
        break ;
    end
end
x_next
counter
figure(1)
ezplot(y(x))
hold on 
plot([-100, 100],[double(y(x_next)), double(y(x_next))],'-r')
double(y(x_next))
figure(2)
plot(show)
pause
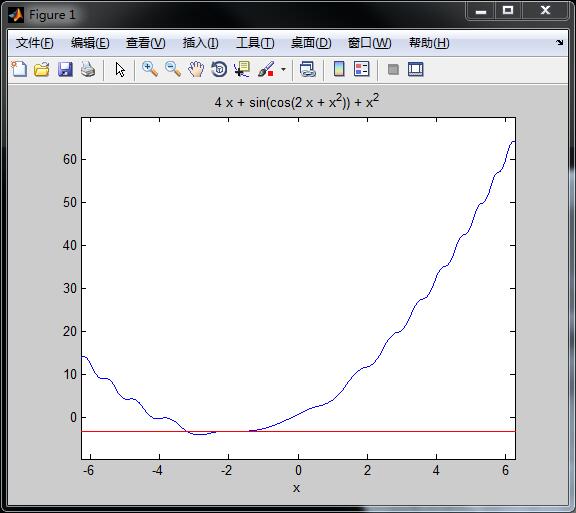
close all

可以看出来，最小值和剃度下降法算出来的最小值并没有重合，此时算法陷入了局部最优点，梯度下降法算出的最小值是y = -3.1586

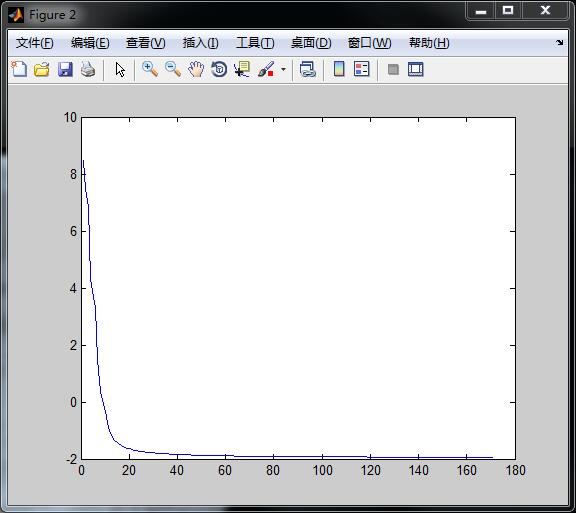
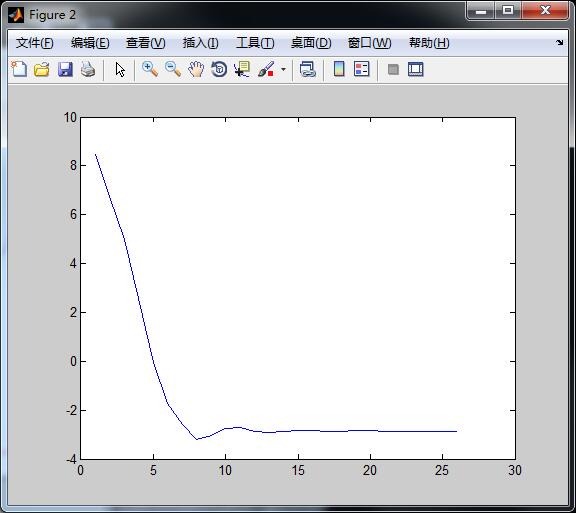
自变量变化曲线如下：

当把冲量项的系数alpha改为0.5时，得出：

此时梯度下降法算出来的最小值为 y = -3.9611,从图中也可以看出已经是达到了函数最低点了。
自变量变化曲线如下：

总结上面的实验，可以看出，加入冲量项可以缓解梯度下降法陷入局部最优的风险。