训练集，测试集，检验集的区别与交叉检验

前言

在机器学习中，不可避免要接触到训练集，测试集以及检验集，这些数据集各有各的作用，为机器学习算法的泛化保驾护航，这里结合《Deep Learning》中的关于训练集，测试集和检验集的讨论，浅谈所见所学。
如有谬误，请联系指正。转载请注明出处。
联系方式：
e-mail: FesianXu@163.com
QQ: 973926198
github: https://github.com/FesianXu

---

训练集和测试集

　　机器学习模型需要训练去更新模型中的各个参数，因此需要提供训练集(Training Set)作为训练样本，假设此训练集由数据生成分布Pdata生成。同时为了描述这个模型的泛化能力，需要一个同样由Pdata生成的测试集(Test Set)进行测试，得出其泛化误差。可以得知，训练集和测试集是独立同分布的，在训练阶段，模型观测不到测试集。

检验集

超参数

　　在讨论检验集之前，有必要先提到超参数(hyperparameter)这个概念。超参数不能或者难以通过机器学习算法学习得出，一般由专家经过经验或者实验选定，如广义线性回归中的多项式次数，控制权值衰减的λ等。容易想象到，不同的超参数选定控制了模型的容量和泛化能力，决定了模型的性能，事实上，超参数的调试(Tuning of the hyperparameter)是机器学习中很关键的一部分。
　　这里我们假想一个场景：

我们有多个待选的权值衰减因子λ,分别是λ1,⋯,λn，这些λ的不同选择代表了一个模型的不同超参数状态，其中有一个可能性能比较优的超参数，为了得到这个较为优的超参数，我们需要在多个[训练集,测试集]元组上训练测试，寻找最小的泛化误差，直到找到合适的超参数为止。

　　由于监督数据的获取困难，一般来说没有那么多数据用来划分这个元组，因此一般的做法是：

将数据集按一定比例划分为训练集（大类）和测试集（Test set），其中测试集只在最后的测试泛化误差的时候才能被模型观察到，而在训练集（大类）中又将其按一定比例划分为训练集(Training Set)和检验集(validation set)，其中训练集用于模型训练，检验集用于寻找最佳的超参数。一般模型会在训练集上训练多次，在检验集上检验多次，直到得到满意的检验误差，然后才能交给测试集得出泛化误差。

交叉检验（Cross Validation）

　　在实际应用中，因为数据集的数量限制，常常采用交叉检验作为检验手段1，其中k折交叉检验(k-folds cross validation)最为常用，其中k=10最为常见。其方法十分简单，就是将训练集（大类）均分为K份，然后分别取出其中的第i个作为检验集，其余的i−1作为训练集训练，然后再检验集上检验。进行了K次该操作之后，采用平均值作为最终的交叉验证误差（CV Error），用于选择模型。

CVError=1K∑i=1KLi

其中Li是第i检验集的平均误差

Li=1m∑j=1m(yj^−yj)2,其中m是第i检验集的样本数量

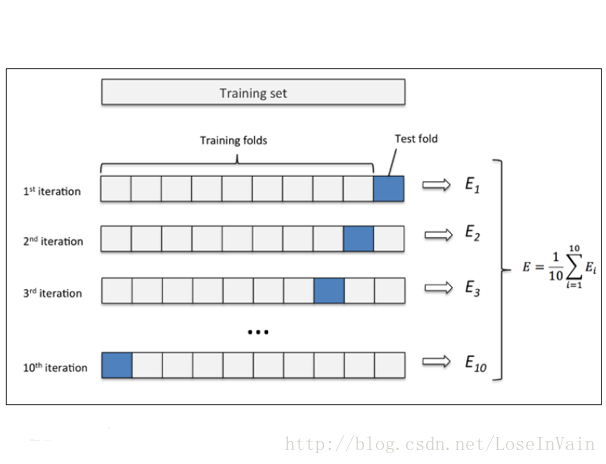
总结

　　在这篇文章里，主要介绍了训练集，检验集，测试集之间的关系，以及引进检验集的目的：就是为了多次比较，得出较好的超参数，进行模型选择。

---

1. 当给定数据集D对于简单的训练/测试或训练/验证分割而言太小难以产生泛化误差的准确估计时（因为在小的测试集上,L可能具有过高的方差)，常常采用交叉验证。 ↩