深度学习中激活函数的选择
前言
在神经网络中,有线性部分,也存在激活函数作为线性部分的非线性激活,这里的激活函数往往是非常重要的,合适的选用有助于提高整个神经网络的性能,这里根据网络的一些所见所学和自己的理解,结合上一篇关于反向传播算法的内容,浅谈下激活函数的选择。
如有谬误,请联系指正。转载请注明出处。
联系方式:
e-mail: FesianXu@163.com
QQ: 973926198
github: https://github.com/FesianXu
基本神经元
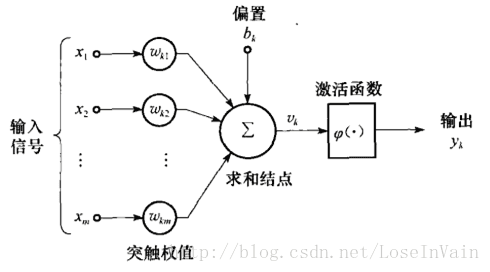
典型的神经元单元是由Rosenblatt提出的Rosenblatt感知器,而其基于McCulloch-Pitts模型,其神经元基本结构如下所示:
典型的神经元具有输入端,偏置端,求和节点(线性部分)和激活函数(非线性部分),用公式表示为:
其中
不难看出,在求和节点之前,其实就是线性部分,而激活函数的作用,就是将线性部分进行非线性映射。联系到SVM中的kernel函数,可以明白这个激活函数使得神经网络具有了非线性分类的能力。实际上,神经网络的拟合能力是相当强悍的,具有一定层次的神经网络甚至可以拟合任何函数。
激活函数
激活函数的主要任务,正如刚才所说的,正是非线性映射,那么就存在很多符合条件的激活函数可供挑选了,而这些激活函数各有优缺点,值得探讨。
Sigmoid函数
sigmoid激活函数是很经典的激活函数,其基本表达式如下:
其导数为:
图像很容易绘制出来,如下所示
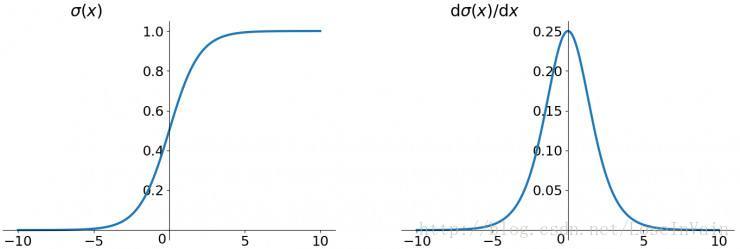
可以看出来,当输入值,也就是线性部分越大或者越小时,其导数越小。让我们回到反向传播算法中的参数更新部分,我们考察式子:
而参数更新的式子为:
可以看出,当
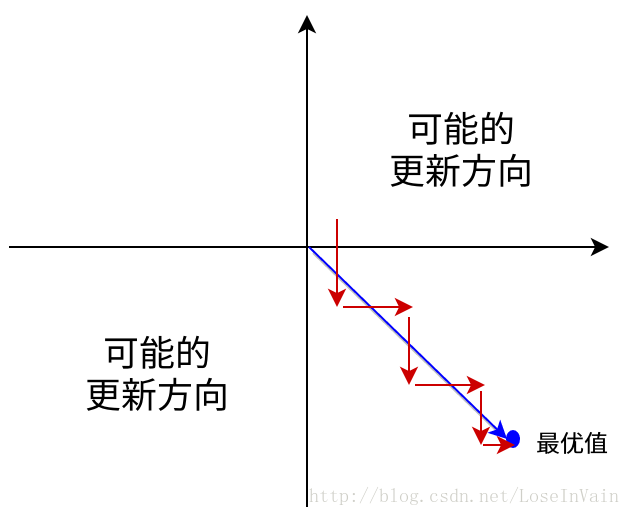
梯度消散是一个很严重的问题,直接导致了网络层数不能加深。但是,sigmoid激活函数不只是有这个问题,我们还要注意到,sigmoid激活函数的输出是非0均值的分布(zero-mean, zero-centered),也就是说,sigmoid函数输出的总是大于0的值,这里有个结论,就是如果所有的输入或者输出(这里的输出相当于下一层的输入)都是负数或者正数,那么对其的边的权值的导数就总是正数,这样会导致产生阶梯式的参数更新,使得参数更新速度变慢1。
特别需要注意的是,对于两类分类的激活来说,sigmoid是softmax的弱化版,因此sigmoid的输出可以看成是概率分布。
tanh函数
tanh函数也称为双曲线函数,函数形式为:
图像为:
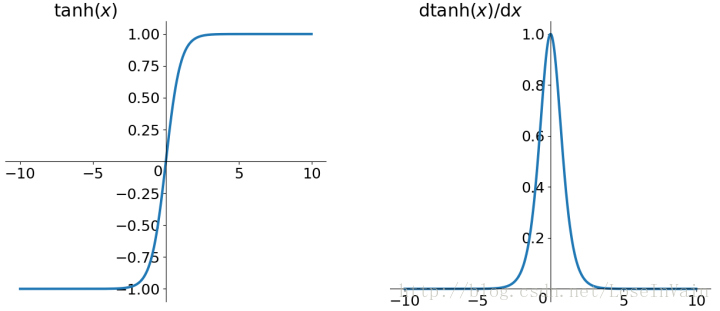
从图上不难看出,tanh是0均值输出的,解决了zero-center问题,但是仍存在梯度消失的问题。
ReLU函数系
ReLU函数称为修正线性单元(Rectified Linear Units),是一种常用于深层网络的激活函数,具有计算简单,可以避免梯度消失等有点。
ReLU函数
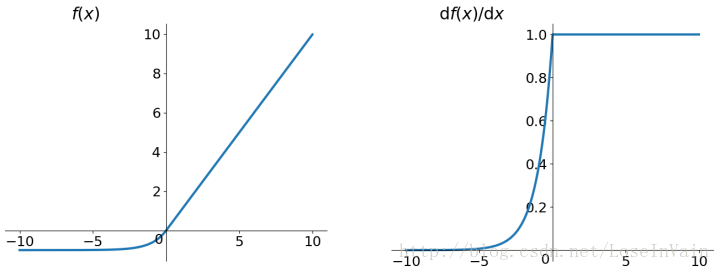
传统的ReLU函数形式为:
图像为:
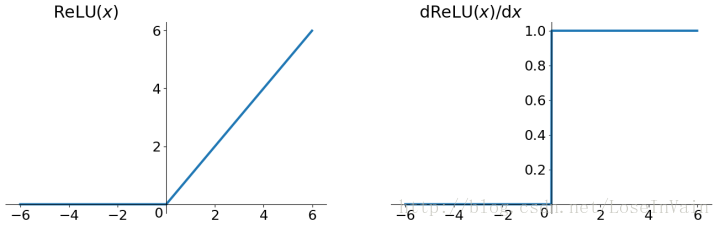
解决了梯度消失的问题,计算速度快,收敛速度远高于sigmoid和tanh,其作为最终输出,非线性程度不足,而且不具有值范围规整的作用。(待求证)其输出仍不是zero-center的,同时也会出现Dead ReLU的问题,指的是某些神经元可能永远都不会被激活,导致参数永远不会被更新。导致的原因有:
非常凑巧的参数初始化,比如
∂C∂wljk=∂C∂zlj∗∂zlj∂wljk=al−1k∗δlj=al−1k∗∑k(δl+1k∗wl+1kj∗σ′(zlj))
中的∑k(δl+1k∗wl+1kj∗σ′(zlj)) 所有的zlj 都处在非激活区,导致∂C∂wljk=0 ,使得参数不更新。学习率Learning rate太高。
ELU函数(Exponential Linear Units)
图像如:
可以看出,其符合zero-center的输出。没有Dead ReLU问题(因为其没有非激活区)
PReLU函数(Parametric ReLU)
其中的
PReLU其中包含了Leaky ReLU,表达式为:
图像如:
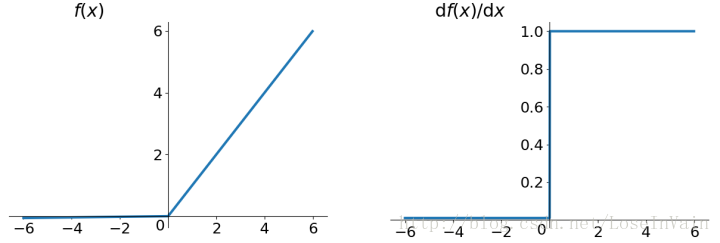
也就是将
- 这里我只能得出最后一层的权值求导结果全为正或者负值,前几层的权值求导结果一部分还会包括权值本身,因此不一定全部为正或者负,这里有待探讨。最后一层可以得出
y=σ(w1x1+w2x2+b) ,因此∂y∂w1=σ′(z)x1 ,可知其为恒大于0。 ↩



 浙公网安备 33010602011771号
浙公网安备 33010602011771号