理解多维高斯分布

理解多维高斯分布

前言

在数理统计和机器学习中，经常用到高斯分布，这里根据网上的资源和理解，对多维高斯分布做一个小总结。

如有谬误，请联系指正。转载请注明出处。

联系方式：
e-mail: FesianXu@163.com
QQ: 973926198
github: https://github.com/FesianXu

---

一维高斯分布

标准的一维高斯分布是0均值和单位方差的，数学形式如(1)：

p(x)=12π−−√exp(−x22)(1)$$\begin{array}{}\text{(1)}& p(x)=\frac{1}{\sqrt{2\pi }}exp(-\frac{x^2}{2})\end{array}$$

为了扩展成一般的一维高斯分布，我们引入一个线性变换x:=A(x−μ)$x:=A(x-\mu )$，结合(1)，有：

p(x)=|A|2π−−√exp(−A2(x−μ)22)(5)(2)$$\begin{array}{}\text{(2)}& \begin{array}{}\text{(5)}& p(x)& =\frac{|A|}{\sqrt{2\pi }}exp(-\frac{A^2(x-\mu {)}^2}{2})\end{array}\end{array}$$

令σ=1/A$\sigma =1/A$，式(2)变为:

p(x)=1σ2π−−√exp(−(x−μ)22σ2)(3)$$\begin{array}{}\text{(3)}& p(x)={\displaystyle \frac{1}{\sigma \sqrt{2\pi }}}exp(-\frac{(x-\mu {)}^2}{2{\sigma }^2})\end{array}$$

从这里可以看出A$A$和σ$\sigma$存在关系。在系数前乘上|A|$|A|$是为了整个分布的积分为1。这里的|⋅|$|\cdot |$表示绝对值，在多变量下，则表示行列式。

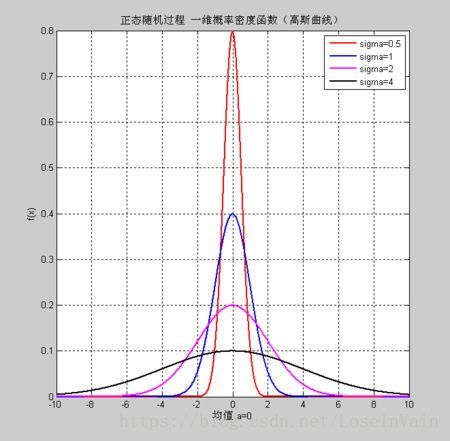
在一维高斯分布上，通过调整均值μ$\mu$和方差σ2${\sigma }^2$可以调整分布的形状，使得其向左右平移，或者拉伸其”顶峰”。

多维高斯分布

多维高斯分布其变量为n$n$维变量，每个变量之间可能会存在关系，为了描述这种关系，我们引入了协方差矩阵Σ$\mathrm{\Sigma }$，其大小为n×n$n\times n$，其中每一个元素为:

Σi,j=conv(Xi,Xj)=E(XiXj)−E(Xi)E(Ej)(2)(3)(4)$$\begin{array}{}\text{(4)}& \begin{array}{}\text{(2)}& {\mathrm{\Sigma }}_{i,j}& =conv(X_i,X_j)\text{(3)}& & =E(X_i{X}_j)-E(X_i)E(E_j)\end{array}\end{array}$$

我们首先看看标准二维高斯分布的数学表达式(5)，因为是标准二维高斯分布，所以每个变量之间是独立的:

p(x,y)=p(x)p(y)=12πexp(−x2+y22)(5)$$\begin{array}{}\text{(5)}& p(x,y)=p(x)p(y)=\frac{1}{2\pi }exp(-\frac{x^2+y^2}{2})\end{array}$$

为了向量化公式，用向量v=[x  y]T$\mathbf{\text{v}}=[xy{]}^T$，有：

p(v)=12πexp(−12vTv)(6)$$\begin{array}{}\text{(6)}& p(\mathbf{\text{v}})=\frac{1}{2\pi }exp(-\frac{1}{2}{\mathbf{\text{v}}}^T\mathbf{\text{v}})\end{array}$$

这个时候，用v=A(x−μ)$\mathbf{\text{v}}=\mathbf{\text{A}}(\mathbf{\text{x}}-\mu )$，其中的A$\mathbf{\text{A}}$为v$\mathbf{\text{v}}$中每个分量的线性组合系数，也就是说A$\mathbf{\text{A}}$表示了每个变量的线性关系。有：

p(v)=|A|2πexp(−12(x−μ)TATA(x−μ))(7)$$\begin{array}{}\text{(7)}& p(\mathbf{\text{v}})=\frac{|\mathbf{\text{A}}|}{2\pi }exp(-\frac{1}{2}(\mathbf{\text{x}}-\mu {)}^T{\mathbf{\text{A}}}^T\mathbf{\text{A}}(\mathbf{\text{x}}-\mu ))\end{array}$$

用Σ=(ATA)−1$\mathrm{\Sigma }=({\mathbf{\text{A}}}^T\mathbf{\text{A}}{)}^{-1}$表示其协方差，其中|A|$|\mathbf{\text{A}}|$为行列式，有：

p(v)=12π|Σ|1/2exp(−12(x−μ)TΣ−1(x−μ))(8)$$\begin{array}{}\text{(8)}& p(\mathbf{\text{v}})=\frac{1}{2\pi |\mathrm{\Sigma }{|}^{1/2}}exp(-\frac{1}{2}(\mathbf{\text{x}}-\mu {)}^T{\mathrm{\Sigma }}^{-1}(\mathbf{\text{x}}-\mu ))\end{array}$$

当维度大于2时，情形类似，n$n$维的高斯分布公式为：

p(v)=1(2π)n/2|Σ|1/2exp(−12(x−μ)TΣ−1(x−μ))v∈Rn(9)$$\begin{gathered} \begin{array}{}\text{(9)}& p(\mathbf{\text{v}})=\frac{1}{(2\pi {)}^{n/2}|\mathrm{\Sigma }{|}^{1/2}}exp(-\frac{1}{2}(\mathbf{\text{x}}-\mu {)}^T{\mathrm{\Sigma }}^{-1}(\mathbf{\text{x}}-\mu )) \\ \mathbf{\text{v}}\in {\mathbb{R}}^n\end{array} \end{gathered}$$

多维高斯分布的图像性质

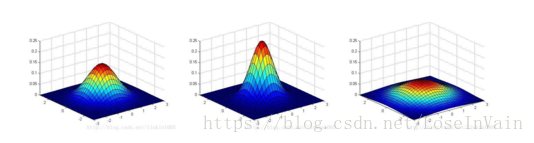
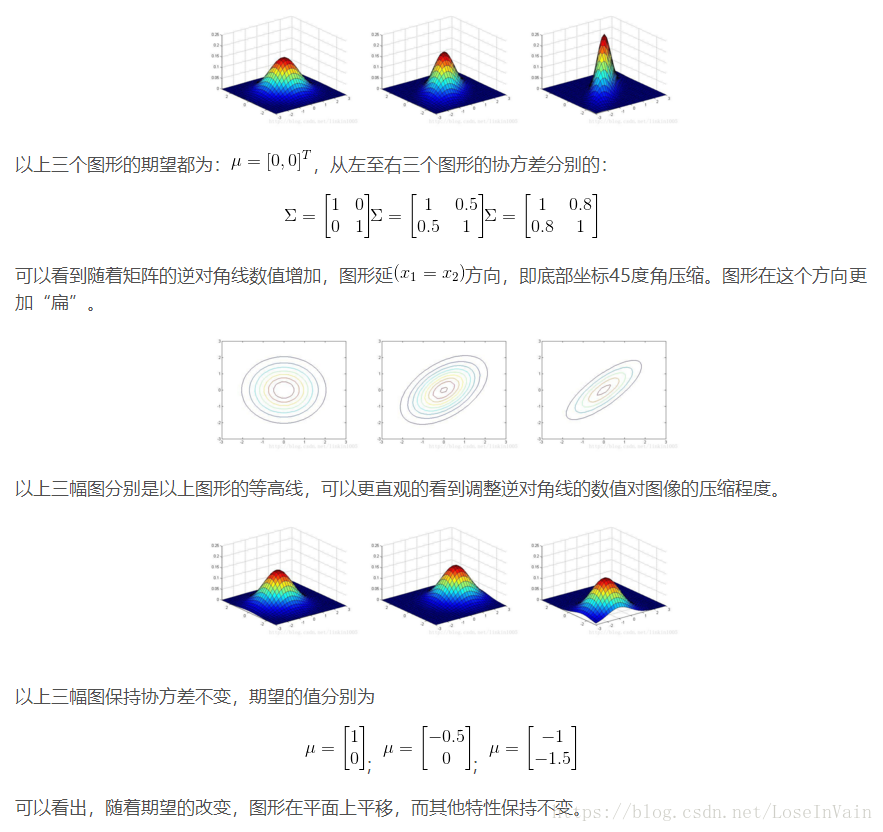
以上三个图形的期望都为：μ=[0,0]T$\mu =[0,0{]}^T$，最左端图形的协方差Σ=I$\mathrm{\Sigma }=I$，中间的Σ=0.6I$\mathrm{\Sigma }=0.6I$，最右端的Σ=2I$\mathrm{\Sigma }=2I$，我们可以看出：当变小时，图像变得更加“瘦长”，而当增大时，图像变得更加“扁平”。

Reference

1. 斯坦福大学机器学习——高斯判别分析
2. 多维高斯分布是如何由一维发展而来的？