pytorch中的L2和L1正则化，自定义优化器设置等操作

在pytorch中进行L2正则化，最直接的方式可以直接用优化器自带的weight_decay选项指定权值衰减率，相当于L2正则化中的$\lambda$，也就是：
$\mathcal{L}_{reg} = ||y-\hat{y}||^2+\lambda||W||^2 \tag{1}$
中的$\lambda$。但是有一个问题就是，这个指定的权值衰减是会对网络中的所有参数，包括权值$w$和偏置$b$同时进行的，很多时候如果对$b$进行L2正则化将会导致严重的欠拟合¹，因此这个时候一般只需要对权值进行正则即可，当然，你可以获取模型中的所有权值，然后按照定义的方法显式地进行处理，得到一个正则损失之后在交给优化器优化，这是一个通用的方法。但是其实还有更为简单的方法，同样在优化器中提供了。

---

torch.optim中包含了很多现成的优化器，包括SGD，Adadelta，Adam，Adagrad，RMSprop等，使用它很简单，你需要传入一个可迭代的参数列表（里面必须都是Variable类型的）进行优化，然后你可以指定一些优化器的参数，如学习率，动量，权值衰减等。例子如：

optimizer = optim.SGD(model.parameters(), lr = 0.01, momentum=0.9,weight_decay=1e-5)
optimizer = optim.Adam([var1, var2], lr = 0.0001)

此外，优化器还支持一种称之为Per-parameter options的操作，就是对每一个参数进行特定的指定，以满足更为细致的要求。做法也很简单，与上面不同的，我们传入的待优化变量不是一个Variable而是一个可迭代的字典，字典中必须有params的key，用于指定待优化变量，而其他的key需要匹配优化器本身的参数设置。我们看一下例子：

optim.SGD([
                {'params': model.base.parameters()},
                {'params': model.classifier.parameters(), 'lr': 1e-3}
            ], lr=1e-2, momentum=0.9)

其中，我们可以看到，传入的list中有两个字典，每一个都是一个独立的参数组，其中每一组中都有一个paramskey，用于指定需要训练的参数，如model.base.parameters()就是base网络中的所有参数，尔后，也可以在每一组内单独设置学习率，权值衰减等。如果不显式地在组内设定，那么就会继承优化器的全局参数，如lr=1e-2,momentum=0.9等，如果组内指定了，那么全局的将不会覆盖掉组内的参数设置。
这样我们就可以灵活的给每一个子网络设定不同的学习率，权值衰减，momentum了，我们也可以给权值设定权值衰减，而不作用与偏置，如：

weight_p, bias_p = [],[]
for name, p in model.named_parameters():
  if 'bias' in name:
     bias_p += [p]
   else:
     weight_p += [p]
# 这里的model中每个参数的名字都是系统自动命名的，只要是权值都是带有weight，偏置都带有bias，
# 因此可以通过名字判断属性，这个和tensorflow不同，tensorflow是可以用户自己定义名字的，当然也会系统自己定义。
optim.SGD([
          {'params': weight_p, 'weight_decay':1e-5},
          {'params': bias_p, 'weight_decay':0}
          ], lr=1e-2, momentum=0.9)

Update 2018-12-12：
有朋友说博文的方法好像报错，我这里又试了下，并没有问题。环境是pytorch 1.0.0，jupyter notebook，ubuntu 16.04。完整测试代码如下：

import torch
import torch.nn as nn
import numpy as np

## build model
class net(nn.Module):
    def __init__(self):
        super().__init__()
        self.fc1 = nn.Linear(100,50)
        self.fc2 = nn.Linear(50,1)
        self.relu = nn.ReLU(inplace=True)
    def forward(self, inputs):
        layer = self.fc1(inputs)
        layer = self.relu(layer)
        layer = self.fc2(layer)
        return layer
## analoy inputs and labels
inputs = np.random.normal(size=(8,100))
inputs = torch.tensor(inputs).float()
labels = np.ones((8,1))
labels = torch.tensor(labels).float()

## update the weights and bias with L2 weight decay 
n = net()
weight_p, bias_p = [],[]
for name, p in n.named_parameters():
    if 'bias' in name:
        bias_p += [p]
    else:
        weight_p += [p]
        
criterion = nn.MSELoss()
logit = n(inputs)
loss = criterion(input=logit, target=labels)
opt = torch.optim.SGD([{'params': weight_p, 'weight_decay':1e-5},
                      {'params': bias_p, 'weight_decay':0}], 
                      lr=1e-2, 
                      momentum=0.9)

## update
opt.zero_grad()
loss.backward()
opt.step()        

请各位试试，谢谢。

Update 2019-9-30

评论区有朋友提到为什么说

很多时候如果对$b$进行L2正则化将会导致严重的欠拟合

这里补充下我的理解。当对b进行了L2正则之后，b的取值范围将变得非常小，接近于0，那么考虑到b是决策平面中的偏置值，那么这个决策平面就会在原点附近。那么现在假设有若干个决策平面，因为b的范围都很小，只能在原点附近，这样子其实是很大程度上限制了这若干决策平面围成决策区域的可能性的。如图所示

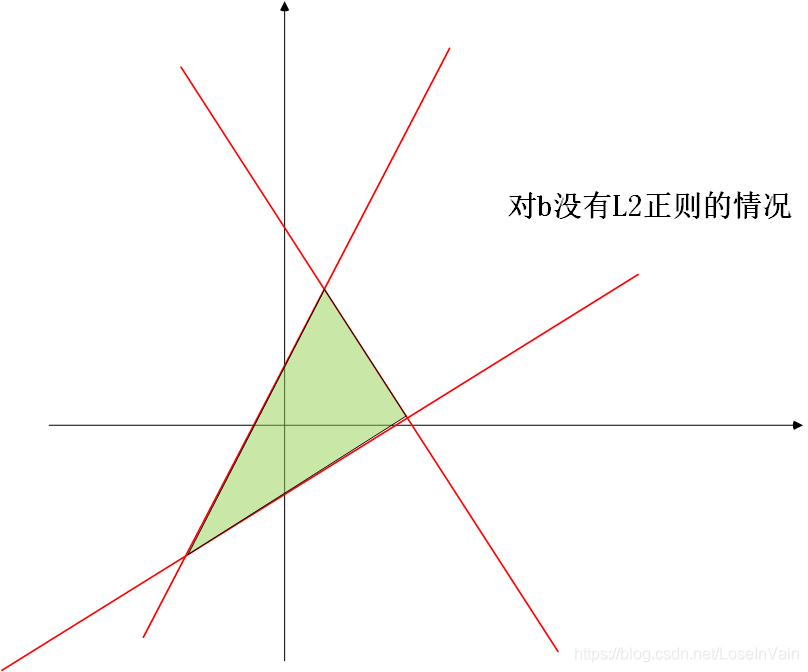
没有对b进行L2正则的时候，因为b的取值范围没有约束在原点附近，那么在对其他决策面不动的情况下，即使是只移动其中某个决策面的b，都可以有很多种决策区域的组合。

然而，如果对b进行了L2正则，那么其决策区域将会变得很小，而且b的可移动范围也是被严重受限了的，因此整个模型的容量对比于w进行L2正则，是受到了很大的削减的。

Reference

[1]. PyTorch Documentation -> torch.optim

---

1. Goodfellow I, Bengio Y, Courville A, et al. Deep learning[M]. Cambridge: MIT press, 2016. ↩︎