贝叶斯曲线拟合

贝叶斯曲线拟合以及对L2正则化的贝叶斯解释

前言

在以前文章中，我们讨论过《概率学派和贝叶斯学派的区别》和《 <机器学习系列> 线性回归模型》，这里我们讨论下曲线拟合问题中的数据点的噪声问题，以及根据贝叶斯理论的L2正则化解释。

如有谬误，请联系指正。转载请注明出处。

联系方式：
e-mail: FesianXu@163.com
QQ: 973926198
github: https://github.com/FesianXu

曲线拟合问题

这里的曲线指的是多项式曲线（polynomial curve）1，如下图所示：

在这里插入图片描述

一般来说，概率学派按照最小化平方和误差函数，如下所示，来进行参数的学习的。
(1.1)Tθ=arg⁡min⁡θL(y^,y)y^j=∑i=0Nθix(i,j)i=y(x;θ)L(y^,y)=12∣∣y^−y∣∣2 \mathcal{T}_{\theta} = \arg \min_{\theta} \mathcal{L}(\hat{y},y) \\ \hat{y}_j = \sum_{i=0}^N \theta_i x_{(i,j)}^{i} = y(x;\theta)\\ \mathcal{L}(\hat{y}, y) = \dfrac{1}{2}||\hat{y}-y||^2 \tag{1.1}
x(i,j)x_{(i,j)}表示第jj个样本的第ii维数据值。更新策略采用梯度下降法[4]即可更新参数，达到收敛。

用概率角度看待曲线拟合，考虑下噪声吧~

但是按照上面策略进行曲线拟合是没有考虑到数据的不确定性（uncertainty）的，这种不确定性体现在数据是添加了噪声的，而基于直接估计出一个点，然后直接拟合的方式没有考虑到这种噪声。为了描述这种不确定性，我们接下来以一种概率的角度去看待曲线拟合问题。

假设我们通过多项式模型预测出来的并不是一个单纯的数字，而是一个分布，一般来说我们将其假设为是一个均值为tt（也就是预测目标值），方差为σ2\sigma^2（β=1σ2\beta=\dfrac{1}{\sigma^2}，β\beta称之为精确度precision），因此预测出来的分布如下式所示：
(1.2)p(t∣x,w,β)=N(t∣y(x,w),β−1) p(t|x, \textbf{w}, \beta) = \mathcal{N} (t|y(x, \textbf{w}), \beta^{-1}) \tag{1.2}
我们之所以假设为是高斯分布，是因为我们假设数据添加的噪声是高斯噪声，既是：
(1.3 数据的噪声分解模型)xobserve=xreal+N(μ,σ2) \mathbf{x}_{\rm{observe}} = \mathbf{x}_{\rm{real}}+\mathcal{N}(\mu,\sigma^2) \tag{1.3 数据的噪声分解模型}
图像看起就更加直观了：

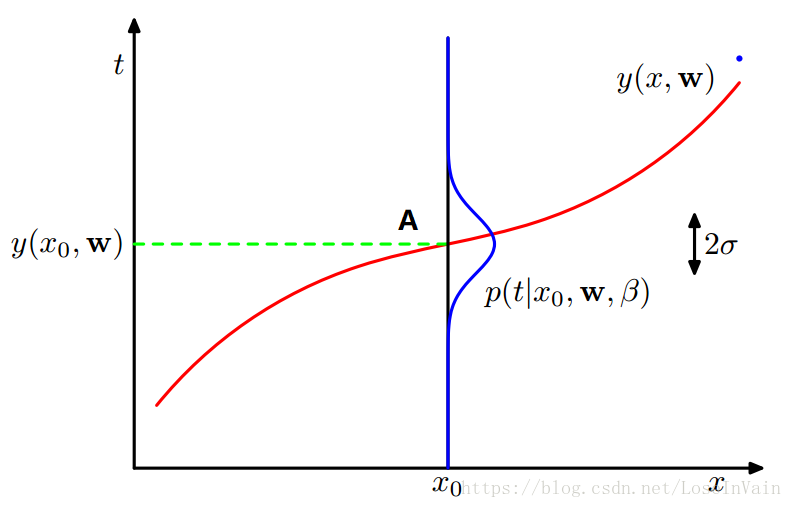
在这里插入图片描述

可以看出，对于某一个预测，其为一个分布（蓝色线），其中预测的均值的预期就是观察值点A，可以看出，参数β\beta决定了其置信范围2σ2\sigma的大小。这个2σ2\sigma的范围可以认为是认为假设的，噪声的主要范围。

如果采用频率学派中的观点，那么就会采用极大似然法进行参数估计。似然函数如下所示：
(1.4)p(t∣x,w,β)=∏i=0NN(tn∣y(xn,w),β−1) p(\textbf{t}|\textbf{x},\textbf{w}, \beta) = \prod_{i=0}^N \mathcal{N} (t_n | y(x_n, \textbf{w}), \beta^{-1}) \tag{1.4}
为了计算方便转化为对数似然后，有：
(1.5)L=ln⁡p(t∣x,w,β)=−β2∑n=1N{y(xn,w)−tn}2+N2ln⁡β−N2ln⁡(2π) \mathcal{L} = \ln p(\textbf{t}|\textbf{x},\textbf{w}, \beta) \\ = -\dfrac{\beta}{2} \sum_{n=1}^N \{y(x_n, \textbf{w})-t_n\}^2 + \dfrac{N}{2}\ln \beta - \dfrac{N}{2} \ln (2\pi) \tag{1.5}
为了估计出w\mathbf{w}，我们用L\mathcal{L}对w\mathbf{w}求偏导数，并且令其为0。我们可以发现(1.5)中的后两项和w\mathbf{w}并没有关系，因此可以舍弃。同时，因为β\beta的取值并不会影响w\mathbf{w}的极值点，因此可以令其为β=1\beta=1。最终，我们有：
(1.6)L=−12∑n=1N{y(xn,w)−tn}2T=max⁡wL=min⁡w−L \mathcal{L} = -\dfrac{1}{2} \sum_{n=1}^N \{y(x_n, \textbf{w})-t_n\}^2 \\ \mathcal{T} = \max_{\mathbf{w}} \mathcal{L} = \min_{\mathbf{w}} \mathcal{-L} \tag{1.6}
不难发现，其实(1.6)式子就是平方和损失，因此我们得出结论：
∇\nabla平方和损失，是在假设数据噪声符合0均值高斯分布的情况下推导出的。∇\nabla

当然，这里的精度β\beta也可以用最大似然法估计，有：
(1.7)1β^=1N∑n=1N{y(xn,w)^−tn}2 \frac{1}{\hat{\beta}} = \frac{1}{N} \sum_{n=1}^N \{y(x_n,\hat{\mathbf{w})}-t_n\}^2 \tag{1.7}
其中的w^\hat{\mathbf{w}}是对权值的估计。

对参数引入先验假设，向着贝叶斯的更进一步

注意到我们之前讨论的都是没有对参数w\mathbf{w}进行任何假设的，也就是说其可以符合任何分布。这个很不贝叶斯，如果我们能对参数引入合理的先验假设，那么就能提高其泛化性能[5]。我们不妨假设w\mathbf{w}符合高斯分布，其均值为0，方差为一个对角矩阵（既是假设每个参数之间独立，其中α\alpha控制了每个参数的range），数学表达为：
(2.1 对参数的先验假设)p(w∣α)=N(w∣0,α−1I)=(α2π)(M+1)/2exp{−α2wTw} p(\mathbf{w}|\alpha) = \mathcal{N}(\mathbf{w}|\mathbf{0},\alpha^{-1}\mathbf{I}) \\ = (\frac{\alpha}{2\pi})^{(M+1)/2} \rm{exp}\{-\frac{\alpha}{2}\mathbf{w}^T\mathbf{w}\} \tag{2.1 对参数的先验假设}
其中MM为多项式次数。如同α\alpha这样的，控制着整个模型的超空间形状的参数，称之为超参数(hyperparameters)。
引入了这个先验假设后，我们模型的后验：
(2.2)p(w∣x,t,α,β)∝p(t∣x,w,β)p(w∣α) p(\mathbf{w}|\mathbf{x},\mathbf{t},\alpha,\beta) \propto p(\mathbf{t}|\mathbf{x},\mathbf{w},\beta)p(\mathbf{w}|\alpha) \tag{2.2}
我们现在可以在给定了训练集{x,t}\{\mathbf{x},\mathbf{t}\}的情况下，通过找到一个最可能的w\mathbf{w}来估计出w\mathbf{w}。换句话说，我们可以最大化这个后验概率，这个技术称之为最大后验概率法(MAximum Posterior,MAP)。取(2.2)的负对数，我们有:
(2.3)ln⁡p(w∣x,t,α,β)∝ln⁡p(t∣x,w,β)+ln⁡p(w∣α) \ln{p(\mathbf{w}|\mathbf{x},\mathbf{t},\alpha,\beta)} \propto \ln{p(\mathbf{t}|\mathbf{x},\mathbf{w},\beta)}+\ln{p(\mathbf{w}|\alpha)} \tag{2.3}
结合(1.6)和(2.1)，舍弃掉和w\mathbf{w}无关的项之后，我们有：
β2∑n=1N{y(xn,w)−tn}2+α2wTw⇒12∑n=1N{y(xn,w)−tn}2+αβwTw \frac{\beta}{2}\sum_{n=1}^N \{y(x_n,\mathbf{w})-t_n\}^2+\frac{\alpha}{2}\mathbf{w}^T\mathbf{w} \\ \Rightarrow \frac{1}{2}\sum_{n=1}^N \{y(x_n,\mathbf{w})-t_n\}^2+\frac{\alpha}{\beta}\mathbf{w}^T\mathbf{w}
令γ=αβ\gamma=\dfrac{\alpha}{\beta}，于是我们就有了在正则项中最常见到的L2正则项γ2wTw\dfrac{\gamma}{2}\mathbf{w}^T\mathbf{w}了。于是我们得到结论：
∇\nabla在贝叶斯理论中，L2正则项是在参数w\mathbf{w}符合0均值高斯分布的情况下推导出来的，其系数γ\gamma决定了正则的程度。∇\nabla

最终一步，贝叶斯曲线拟合

在上一步中，虽然我们根据最大后验法估计出了w\mathbf{w}，但是对于曲线拟合来说，这并不是我们的最终目标，我们的最终目标是估计出目标值t^\hat{\mathbf{t}}出来。在完全的贝叶斯处理过程中，我们的估计出来的w\mathbf{w}是一个分布，为了得到预测值t^\hat{\mathbf{t}}，我们要用概率的加法和乘法法则，对所有可能的w\mathbf{w}进行积分，得到目标值。这个操作将在贝叶斯理论中一直沿用。
具体到我们的曲线拟合的例子，当我们给定了训练集{x,t}\{\mathbf{x},\mathbf{t}\}的时候，当输入一个新的输入xx的时候，我们期望得到其预测值tt。也就是说我们需要得出p(t∣x,x,t)p(t|x,\mathbf{x},\mathbf{t})，由概率的基本和积定理有：
(3.1)p(t∣x,x,t)=∫p(t∣x,w)p(w∣x,t)dw p(t|x,\mathbf{x},\mathbf{t}) = \int p(t|x,\mathbf{w})p(\mathbf{w}|\mathbf{x},\mathbf{t}) \rm{d} \mathbf{w} \tag{3.1}
因为采用了共轭先验[6]假设，因此我们的后验概率同样是一个高斯分布。也即是：
(3.2)p(t∣x,x,t)=N(t∣m(x),s2(x)) p(t|x,\mathbf{x},\mathbf{t}) = \mathcal{N}(t|m(x),s^2(x)) \tag{3.2}
这个时候，均值和方差可以给定为[1] page 31（暂时并不知道怎么算出来的）
(3.3)m(x)=βϕ(x)TS∑n=1Nϕ(xn)tn m(x) = \beta \phi(x)^T \mathbf{S} \sum_{n=1}^N \phi(x_n) t_n \tag{3.3}
(3.4)s2(x)=β−1+ϕ(x)TSϕ(x) s^2(x) = \beta^{-1}+\phi(x)^T\mathbf{S}\phi(x) \tag{3.4}
(3.5)S−1=αI+β∑n=1Nϕ(xn)ϕ(x)T \mathbf{S}^{-1} = \alpha\mathbf{I}+\beta \sum_{n=1}^N \phi(x_n)\phi(x)^T \tag{3.5}
其中的ϕ(x)=xi,i=0,⋯&ThinSpace;,M\phi(x)=x^i,i=0,\cdots,M。
可以观察到，这个均值m(x)m(x)是取决于xx的，在式子(3.4)中的第一项，代表了因为目标的噪声所带来的不确定性。而第二项，表示了因为w\mathbf{w}的不确定所带来的不确定性，这个正是贝叶斯处理所带来的结果。下图的绿线表示了生成样本的基线，蓝色样本表示基线上添加高斯噪声的结果，红线是预测的均值，红区域是正负1个标准差的区域。
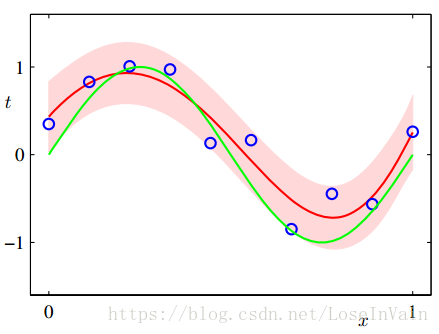
在这里插入图片描述

Reference

[1] Bishop C M. Pattern recognition and machine learning (information science and statistics) springer-verlag new york[J]. Inc. Secaucus, NJ, USA, 2006.
[2] 《概率学派和贝叶斯学派的区别》
[3] 《 <机器学习系列> 线性回归模型》
[4] 《随机梯度下降法，批量梯度下降法和小批量梯度下降法以及代码实现》
[5] 《机器学习模型的容量，过拟合与欠拟合》
[6] 《先验概率、后验概率以及共轭先验》

  1. A curve obtained by fitting polynomials to each ordinate of an ordered sequence of points. 指的是用多项式函数f(X;θ)=∑i=0Nθixii,X∈RNf(\textbf{X}; \theta)=\sum_{i=0}^N \theta_i x_i^{i}, \textbf{X} \in \mathbb{R}^N。其中如果指数全部变为1而不是ii，则退化为线性回归。 ↩︎

posted @ 2018-09-23 15:55  FesianXu  阅读(551)  评论(0)  编辑  收藏  举报