二叉树的遍历，递归与迭代的解法

二叉树的遍历，递归与迭代的解法

FesianXu, 19' 9.29 at UESTC

前言

树结构是一种非线性的数据结构，而二叉树是树结构中常见的一种树，这章我们考虑如何对二叉树进行元素的遍历，在这里我们会分别考虑递归和迭代两种不同的解法。

---

$\nabla$ 目录 $\nabla$

文章目录

• 前言
• @[toc]
• 所谓二叉树以及其遍历
• 二叉树
• 遍历的策略
• 代码平台
• 递归方案
• 迭代方案
• 前序遍历
• 中序遍历
• 后序遍历
• Reference

所谓二叉树以及其遍历

二叉树

相对于队列，栈这种抽象的线性数据结构来说，树是一种非线性的数据结构，而二叉树是树的一种经典的，常见的种类。对二叉树的遍历是一个很基础也很重要的问题，遍历指的是依据一定的顺序对树的元素进行访问，最后需要访问到整个树的所有元素。一般来说，对树的遍历可以有递归和迭代两种不同的实现，通常来说递归的解法直接明了，但是在树的深度很大的时候，容易导致stack overflow；而迭代方法通常更快，更节省内存，但是通常理解起来没有递归方法简单。

要描述一棵树，首先其单元结构可以用一个结构体描述，如：

 struct TreeNode {
     int val;
     TreeNode *left;
     TreeNode *right;
     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 ;

其中，一棵树的叶子节点指的是其左右节点皆为空

node->left == NULL && node->right == NULL ;

遍历的策略

对于每个非叶子节点而言，其都有根节点D， 左节点L和右节点R，如果遍历的时候只考虑从左到右的这种方向，我们可以有三种排列

1. DLR，前序遍历
2. LDR，中序遍历
3. LRD，后序遍历

我们发现，我们是根据访问D的位置来确定其命名的，这里举几个例子。加入树长成这个样子

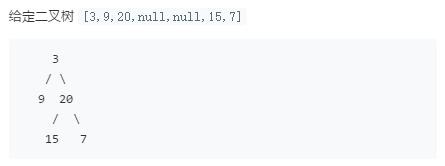
那么其前序遍历结果为： 3 -> 9 -> 20 -> 15 -> 7

中序遍历结果为： 9 -> 3 -> 15 -> 20 -> 7

后序遍历结果为： 9 -> 15 -> 7 -> 20 -> 3

那么针对这三种遍历策略，我们后续进行代码编写分析和实验。

代码平台

本文中代码可在LeetCode中进行运行，大家可以随意选择一个与树相关的题目进行测试代码（LeetCode内部提供了Tree数据结构的支持），比如说笔者是在https://leetcode-cn.com/problems/binary-tree-preorder-traversal/中进行的，我们只需要指定了树的结构（可以通过在控制台指定其树的每个元素，如下图所示），显然只要我们有了目标树的输入，我们便可以开始我们的实验了。

递归方案

对于树的遍历来说，递归方案是很容易理解的，这种方法也是必须要掌握的。

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
		if (!root) return {};
		if (!root->left && !root->right) return {root->val};
		vector<int> vec;
		vec.push_back(root->val);
		auto ret = preorderTraversal(root->left);
		vec.insert(vec.end(), ret.begin(), ret.end());
		auto ret = preorderTraversal(root->right);
		vec.insert(vec.end(), ret.begin(), ret.end());
		return vec;
    }
};

其实还有一种方式，更为简洁：

class Solution {
public:
    void preorderTraversal(TreeNode* root, vector<int> &vec) {
		if (!root) return ;
		vec.push_back(root->val);
		preorderTraversal(root->left);
		preorderTraversal(root->right);
    }
};

我们会发现，决定其顺序的，是ret.push_back(root->val)这句代码的顺序而已。

---

迭代方案

比起递归的方案，迭代的方案去遍历树比较难，在LeetCode中属于中等难度的题目[1,2,3]，不过对其进行理解有助于我们更好的理解树的遍历，因此我们还是要求掌握。

对于迭代方案来说，就不再和递归一样具有一个统一的范式进行求解了。

前序遍历

我们可以用一个LIFO(Last In First Out)的stack进行这个遍历过程的管理，我们采用了c++中的stack数据结构，这个结构是一个操作受限的stack，只能有以下操作

• push， 在stack尾部推入新的元素
• pop， 弹出尾部元素，不返回值
• empty， 判断stack是否为空
• size，stack的大小
• top，读取尾部元素，但是不弹出

利用stack，我们在获取了一个节点之后，对其右节点和左节点进行入栈，当然前提是其节点存在，为什么要反过来入栈呢？因为出栈的顺序是和入栈顺序相反的，因此出栈的时候顺序就是正常的L->R了，对于每个节点都这样去考虑其左右节点，我们就得到了整个先序遍历列表。代码如下。

    vector<int> preorderTraversal(TreeNode* root) {
        if (!root) return vector<int>();
        stack<TreeNode*> stack;
        vector<int> ret;
        stack.push(root);
        while (!stack.empty()) {
            auto curr = stack.top();
            stack.pop();
            ret.push_back(curr->val);
            if (curr->right) 
                stack.push(curr->right);
            if (curr->left) 
                stack.push(curr->left);
        }
        return ret;
        
    }

中序遍历

我们在中序遍历中，有：

​ 对于某个节点A而言，在访问A之前，肯定会先访问A的左子树的所有元素

中序遍历同样采用了栈stack作为储存节点的数据结构，但是因为中序遍历LDR需要首先访问左节点，因此一开始需要将根节点的所有左节点先进行入栈，如#8-#11所示。然后，在#12-#21对栈中的元素进行出栈。一开始在没有其他元素入栈的时候显然是叶子节点的左节点7首先出栈，然后因为是叶子节点，因此没有任何的其他后继节点了，继续循环。

在下个循环中，出栈的是倒数4，这个时候，节点4的左子树和自己以及被访问了，需要考虑其右子树了，那么将node = node->right 考虑其右子树，因为在右子树中，我们同样要根据中序遍历的要求，首先访问右子树节点的左子树节点，所以这个时候，代码#16-#19就在对其左子树进行入栈，和#8-#11相似。

Fig 1. 首先将根节点的所有左节点入栈。

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        if (!root) return vector<int>();
        stack<TreeNode*> stack;
        vector<int> ret;
        while (root) {
            stack.push(root);
            root = root->left;
        } // 将根节点的所有左子树迭代入栈
        while (!stack.empty()) {
            auto node = stack.top();
            stack.pop();
            ret.push_back(node->val);
            node = node->right; // 切换到右子树
            while (node) {
                stack.push(node);
                node = node->left;
            }
        }
        return ret;
    }
};

中序遍历比起前序遍历来说，难上了些。总得来说，基于迭代的中序遍历可以用模版如下来解决：

class Solution {
public:
    vector<int> inorder(TreeNode* root) {
        if (!root) return vector<int>(); // 边界条件注意
        stack<TreeNode *> s; // 一个栈来保存节点的遍历
        vector<int> ret;
        while (!s.empty() || root != NULL) {
            while (root) {
                s.push(root);
                root = root->left;
            }
            root = s.top();
            cont.pop(); // 弹出左子树
          	// 这里插入对左节点L应该进行的处理，比如读取，修改等。如遍历，则是
          	ret.push_back(root->val);
            root = root->right; //将节点更新为右子树
        }
        return ret;
        
    }
};

后序遍历

leetcode官方对这个问题的解决是： 后序遍历 = 宽度优先搜索+逆序输出，代码为：

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        if (!root) return vector<int>();
        
        stack<TreeNode*> stack;
        vector<int> ret;
        stack.push(root);
        while (!stack.empty()) {
            auto node = stack.top();
            stack.pop();
            ret.push_back(node->val);
            if (node->left) 
                stack.push(node->left);
            if (node->right)
                stack.push(node->right);
        }
        std::reverse(ret.begin(), ret.end());
        return ret;
    }
};

其实是逆前序遍历啦。

Reference

[1]. https://leetcode-cn.com/problems/binary-tree-preorder-traversal/

[2]. https://leetcode-cn.com/problems/binary-tree-inorder-traversal/

[3]. https://leetcode-cn.com/problems/binary-tree-postorder-traversal/