[leetcode刷题笔记] 杨辉三角 I&II

题目地址：

1. https://leetcode-cn.com/problems/pascals-triangle/ 杨辉三角 I
2. https://leetcode-cn.com/problems/pascals-triangle-ii/ 杨辉三角 II

题目内容：

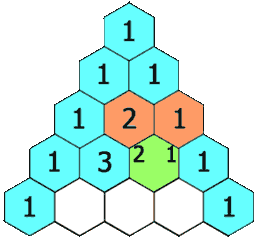
在杨辉三角中，每个数是他的左上方和右上方的数的和，公式表达为：
$f(i,j) = f(i-1,j-1)+f(i-1,j) \tag{1}$

---

题目内容：

• 杨辉三角 I: 给定一个非负整数 numRows，生成杨辉三角的前 numRows 行。

示例：

输入: 5
输出:
[
[1],
[1,1],
[1,2,1],
[1,3,3,1],
[1,4,6,4,1]
]

这题最直观的方法是采用递推式(1)，根据上一行的数据直接产生下一行的数据就行了，比较简单，见代码：

class Solution {
public:
    vector<vector<int>> generate(int numRows) {
        // f(i,j) = f(i-1, j-1)+f(i-1,j)
        if (numRows <= 0)
            return vector<vector<int>>();
        vector<vector<int>> ret;
        ret.push_back(vector<int>{1});
        for(int layer = 1; layer < numRows; layer++){
            vector<int> tmp(layer+1);
            tmp[0] = 1;
            tmp[layer] = 1;
            for (int element = 1; element < layer; element++)
                tmp[element] = ret[layer-1][element-1]+ret[layer-1][element];
            
            ret.push_back(tmp);
        }
        return ret;
    }
};

容易知道，此代码的时间复杂度是$\mathcal{O}(n^2)$，空间复杂度为$\mathcal{O}(n^2)$

如果我们输入行数，只需要函数输出特定行数的排列，而不需要整个前n行的排列，我们可以怎么做呢？当然，我们可以把前n行都计算出来后，取某个行的结果，不过这样的计算复杂度是比较高的，我们可以用一些巧妙些的方法，把计算复杂度和空间复杂度减少，见第二题。

题目内容：

• 杨辉三角II：给定一个非负索引 k，其中 k ≤ 33，返回杨辉三角的第 k 行

示例：

输入: 3
输出: [1,3,3,1]

注意到我们可以把第二题的空间复杂度优化到$\mathcal{O}(n)$，针对指定的第n行，我们只需要线性空间即可。算法流程如下：我们首先初始化出一个数组，这个数组的长度为n+1，对于任意行，总是可以把第一个数初始化为1，假设我们的n=4，于是我们有初始化的数组[1,0,0,0]，我们有如下递推公式：

for (int i = n-1; i > 0; --i)
	v[i] = v[i]+v[i-1];

我们发现，其实是倒过来进行相邻元素叠加的，因为如果是正向叠加，会影响到之前的元素，操作起来比较麻烦些，而倒过来进行则不会这样。于是有：
第一轮

step1: [1, 0, 0, 0] 初始化
step2: [1, 0, 0, 0] 空操作
step3: [1, 0, 0, 0] 空操作
step4: [1, 1, 0, 0]

第二轮

step1: [1, 1, 0, 0] 空操作
step2: [1, 2, 1, 0]

我们注意到有部分0+0的操作是空操作，是不必要的，可以去掉以提高性能。最终，我们的代码如下所示：

class Solution {
public:
    vector<int> getRow(int rowIndex) {
        vector<int> ret(rowIndex+1);
        ret[0] = 1;
        for (int j = rowIndex; j > 0; j--)
            for (int i = rowIndex-j+1; i > 0; --i)
                ret[i] += ret[i-1];
            
        return ret;
        
    }
};

还算是比较精简的，其时间复杂度为$\mathcal{O}(n^2)$，准确的说是$\mathcal{O}(\frac{1}{2}n^2)$，空间复杂度为$\mathcal{O}(n)$。

---

容易出现的问题：

1. 注意边界，为了减少空操作，边界特别要注意。