立体视觉中的对极几何——如何更好更快地寻找对应点

立体视觉中的对极几何——如何更好更快地寻找对应点

2019.10.21 FesianXu

文章目录

• @[toc]
• 前言
• 什么是立体视觉
• 对极几何
• 对极约束
• 本征矩阵
• 去掉归一化坐标系的限制，引入基础矩阵
• Reference

前言

在立体视觉中，我们通过多个摄像机的相互配合，可以获得关于现实生活中物体的一些3D信息，通过这些信息，我们可以对这个物体进行重建，建模等等。而在立体视觉中，对极几何有着非常重要的作用，在本文中，笔者将讨论下立体视觉中的对极几何，如何用对极几何去进行更好更快地寻找不同视图中的对应点。如有谬误，请联系指正。转载请注明出处。

$\nabla$ 联系方式：
e-mail: FesianXu@gmail.com
QQ: 973926198
github: https://github.com/FesianXu

---

什么是立体视觉

立体视觉(Stereo Vision)是什么呢？我们可以这样理解：
$立体视觉(Stereo Vision) = 寻找相关性(Correspondences) + 重建(Reconstruction)$

• Correspondences: 给定一张图片中的像素$P_l$点，寻找其在另一张图片中的对应点$P_r$。
• Reconstruction: 给定一组对应点对$(P_l, P_r)$，计算其在空间中对应点$P$的3D坐标。

Fig 1.1 立体视觉的寻找对应点和重建。

那么，在本文中，其实我们要讨论的内容就属于如何去更好更快地寻找对应点。抱着这个问题，我们正式地开始讨论对极几何吧。

---

对极几何

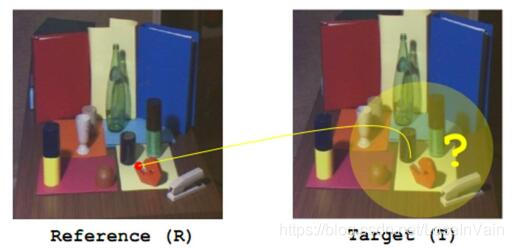
假设我们现在有两张从不同视角拍摄的，关于同一个物体的图片，如Fig 2.1所示，最为朴素的想法就是从一个2D区域中去寻找对应点，这样显然我们的计算复杂度很高，而且还不一定精准，那么我们有没有能够改善这个算法的方案呢？我们能不能对对应点的可能搜索范围进一步缩小呢？答案是可以的。

Fig 2.1 难道我们要从一个2D区域中去寻找对应点？

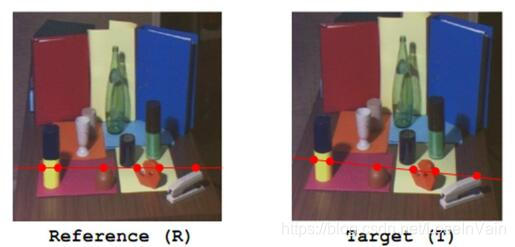
通过对极几何的约束，我们可以把搜索空间限制在一个直线上，我们将这个直线称之为对极线，显然，这样不仅提供了搜索的效率，还提高了搜索的精确度。如Fig 2.2所示。

Fig 2.2 通过对极几何的约束，我们将搜索空间限制在了对极线上。

这个对极几何那么神奇，那到底是什么原理呢？且听笔者慢慢道来。

对极约束

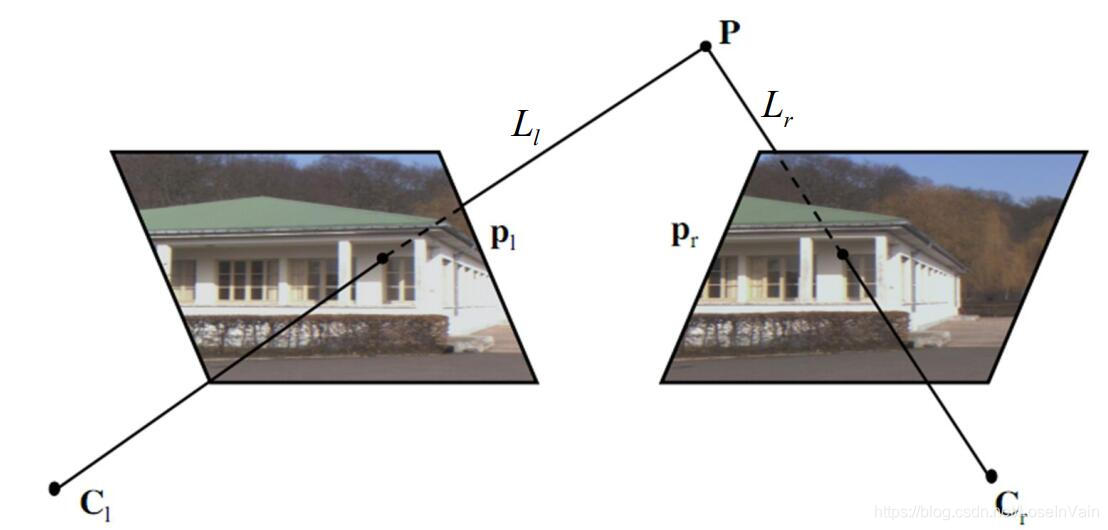
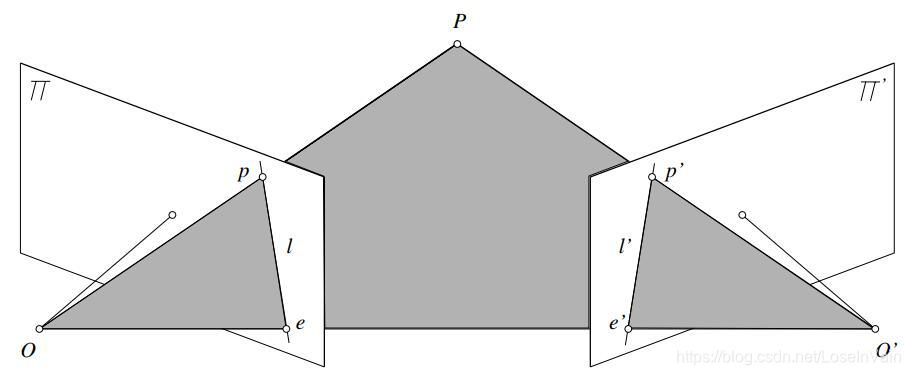
为了简单分析考虑，我们现在只是假设两台摄像机的情况，假设我们已经对摄像机进行了内外参数的标定[2]，也就是说，我们已经知道了摄像机的朝向以及彼此之间的距离，相对位置关系等，同时也知道了内参数，也就是焦距等等。那么我们假设现在这两台摄像机同时对某个现实物体点$P$进行成像，我们有几何关系示意图Fig 2.3。

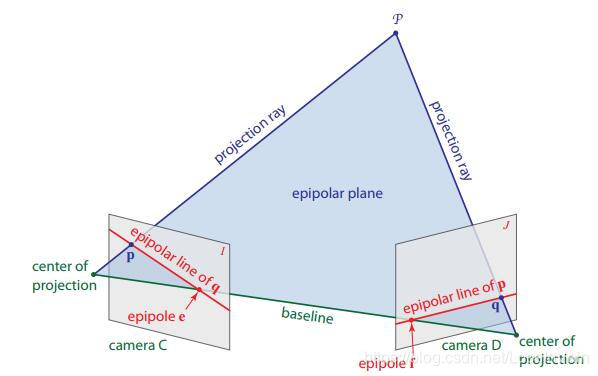
Fig 2.3 对极几何约束，其中P点是实体3D点，O和O'是焦点

在Fig 2.3中，其中的$P = (x,y,z)$是实体3D点，而$O$和$O^{\prime}$是两个摄像机的焦点（对于焦点，读者不妨看成是一个观察者的视角，也就是你可以想象成你在$O$和$O^{\prime}$点观察P点。），而成像平面$\prod$和$\prod^{\prime}$就是我们的成像面，其中面上的$p$和$p^{\prime}$是实体点P的成像对应点，我们需要找的对应关系，其实就是$(p, p^{\prime})$这样的点对。

对于这两个不同的相机坐标系，我们对于这两个成像点有着不同的坐标系表达，让我们分别以各自的焦点为原点，表达这两个点，有：
$\mathbf{p} = \left[ \begin{matrix} p_1 \\ p_2 \\ f \\ \end{matrix} \right] 和 \, \, \mathbf{p^{\prime}} = \left[ \begin{matrix} p_1^{\prime} \\ p_2^{\prime} \\ f^{\prime} \\ \end{matrix} \right] \tag{2.1}$
对于Fig 2.3中的其他几何元素，我们分别给予术语，以方便称呼：

1. 点$e$和点$e^{\prime}$称之为极点(epipole)
2. 线$l$和$l^{\prime}$称之为对极线(epipolar line)，其中$l$是点$p^{\prime}$的对极线，$l^{\prime}$是点$p$的对极线。
3. 焦点之间的连线$OO^{\prime}$称之为基线(Baseline)
4. 平面$POO^{\prime}$称之为对极面(epipolar plane)。

具体的元素位置，我们还能参考图Fig 2.4中的英语标注。

Fig 2.4 对极几何的一些术语。

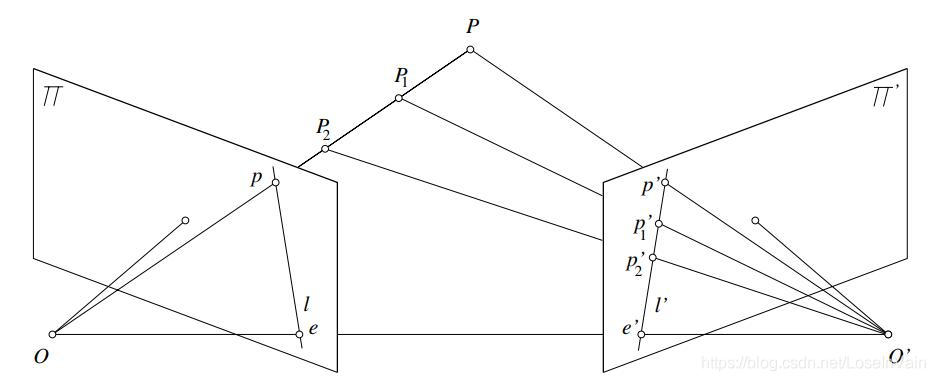
那么由图Fig 2.3我们其实很容易发现，所谓的对极约束，指的就是，成像平面$\prod$上的点$p$，其在$\prod^{\prime}$的对应点$p^{\prime}$必然在其对极线$l^{\prime}$上，这个关系可以由三者共面很容易看出来，其证明可参考[3]。也就是说，对于点$p$，如果我们要搜索其在另一个成像平面上的对应点，无需在整个平面上搜索，只需要在对极线上寻找即可了。如图Fig 2.5所示，我们发现这个几何关系其实是很直观的。

Fig 2.5 一系列实体点以及其在两个摄像机成像平面上的成像点。

再如图Fig 2.6所示，这是个实际图像的例子，我们发现我们刚才在几何上的结论在实际中是成立的。

Fig 2.6 b和c上的对极线以及其对应点的位置。

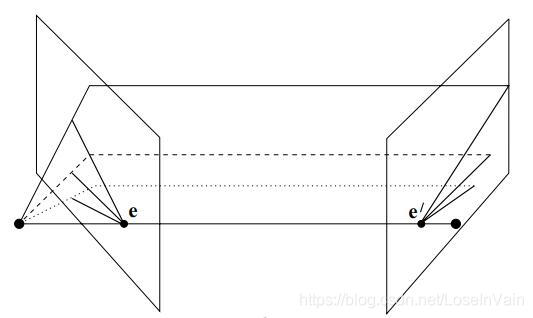
同时，我们要注意到，我们的基线和成像平面的位置是不会改变的（假设不改变摄像机的相对位置的话），那么显然，不管实体点$P$的位置在哪里，所有的对极线都是会经过极点的，如图Fig 2.7所示,其中虚线表示不同的对极面，不管对极面是哪个，都是会经过基线的；相对应的，所有的对极线也是会经过极点的。

Fig 2.7 不同的对极面都会经过基线。

好的，那么我们以上就直觉上讨论了对极约束，那么我们应该怎么用代数的方式去描述这个约束呢？毕竟只有用代数的方式表达，才能进行计算机的编程和实现。为了实现代数化，我们要引入所谓的本征矩阵。我们接下来讨论这个。

---

本征矩阵

还记得公式(2.1)中，我们曾经对两个对应点$p$和$p^{\prime}$进行了坐标表达吗？假设我们现在知道了每台摄像机的内部参数，并且图像坐标已经归一化[4,5]，这里所说的归一化指的是假设存在一个焦距为1的面，如Fig 2.8所示，这里假设焦距为单位长度，是为了后面的分析方便而已，我们将会看到，当考虑实际焦距时，其处理略有不同。进行了归一化之后，我们有
$\begin{aligned}\mathbf{p} &= \mathbf{\hat{p}} \\\mathbf{p}^{\prime} &= \mathbf{\hat{p}}^{\prime}\end{aligned}$
其中$\mathbf{\hat{p}}, \mathbf{\hat{p}}^{\prime}$是图像点的单位坐标向量。

Fig 2.8 相机系统内的物理视网膜平面（也就是实际的成像平面）和归一化成像平面（也就是焦距为1时的成像平面，是假想出来的平面，为了分析方便）。

OK， 不管怎么样，我们继续我们的讨论。我们发现在Fig 2.3中，$\vec{Op}, \vec{O^{\prime}p^{\prime}}$和$\vec{OO^{\prime}}$共面，我们用代数描述就是：
$\vec{Op} \cdot [\vec{OO^{\prime}} \times \vec{O^{\prime}p^{\prime}}] = 0 \tag{2.2}$
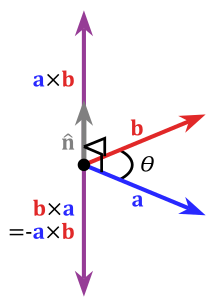
其中，$\times$表示的是向量叉乘，我们知道空间向量叉乘表示求得其在右手坐标系中的正交向量，如图Fig 2.9所示。

Fig 2.9 叉乘的几何意义。

而式子中的点积为0表示了垂直关系，因此式子(2.2)正确表达了我们的对极约束，我们接下来代入坐标。

考虑在$\prod^{\prime}$中表示点$p$，通过坐标的平移和旋转可以容易实现，见：
$\mathbf{q}^{\prime} = \mathbf{R}(\mathbf{p}-\mathbf{t}) \tag{2.3}$
其中$\mathbf{t}$表示平移向量，$\mathbf{R}$表示旋转矩阵。那么反过来有：
$\mathbf{p} = \mathbf{R}^{\mathrm{T}}\mathbf{q}^{\prime}+\mathbf{t} = \mathbf{R}^{\mathrm{T}}(\mathbf{q}^{\prime}+\mathbf{R}\mathbf{t}) \tag{2.4}$
令$R^{\prime} = \mathbf{R}^{\mathrm{T}}$和$s^{\prime} = -\mathbf{R}\mathbf{t}$，我们有(2.4)的简化形式：
$\mathbf{p} = R^{\prime} (\mathbf{q}^{\prime}-s^{\prime}) \tag{2.5}$
考虑公式(2.2)，我们发现：
$\begin{aligned} \vec{Op} &= \mathbf{p} \\ \vec{OO^{\prime}} &= \mathbf{t} \\ \vec{O^{\prime}p^{\prime}} &= \mathbf{p}^{\prime} \end{aligned} \tag{2.6}$
注意到，因为对于垂直关系而言，平移与否没有影响，我们最终有式子：
$\begin{aligned}\mathbf{p} \cdot [\mathbf{t} \times \mathbf{p}^{\prime}] &= 0 \\(\mathbf{R} \mathbf{p}) \cdot [\mathbf{t} \times \mathbf{p}^{\prime}] &= 0 \\(\mathbf{R} \mathbf{p})^{\mathrm{T}} [\mathbf{t} \times \mathbf{p}^{\prime}] &= 0 \\\mathbf{p}^{\mathrm{T}} \mathbf{R}^{\mathrm{T}} [\mathbf{t} \times \mathbf{p}^{\prime}] &= 0 \\\mathbf{p}^{\mathrm{T}} \mathbf{R}^{\mathrm{T}}[\mathbf{t}]_{\times} \mathbf{p}^{\prime} &= 0\end{aligned}\tag{2.7}$
其中，(2.7)第二行的公式表示在另一个成像平面 $\prod^{\prime}$ 表示$\prod$上的坐标，最后一行，我们把叉乘转化成矩阵乘法操作[6]。对于一个$\mathbf{t} = [t_1, t_2, t_3]^{\mathrm{T}}$来说，其叉乘乘子的矩阵乘法形式为：
$[\mathbf{t}]_{\times} = \left[\begin{matrix}0 & -t_3 & t_2 \\t_3 & 0 & -t_1 \\-t_2 & t_1 & 0 \end{matrix}\right]\tag{2.8}$
如果用$\mathcal{E} = \mathbf{R}^{\mathrm{T}}[\mathbf{t}]_{\times}$，我们有：
$(\mathbf{p}^{\mathrm{T}}) \mathcal{E} \mathbf{p}^{\prime} = 0\tag{2.9}$
我们把这里的$\mathcal{E}$称之为本征矩阵(Essential matrix)。

我们发现，这里的旋转矩阵$\mathbf{R}$其实是可以通过相机标定进行外参数估计得到的，同样的，$\mathbf{t}$也是如此。假设，我们现在已知了$\prod$上的点$p$，我们可以令$\mathbf{\mu}_p = (\mathbf{p}^{\mathrm{T}}) \mathcal{E} \in \mathbb{R}^3$，我们知道这个是个常数向量。最终，公式(2.9)可以写成：
$\mathbf{\mu}_p \mathbf{p}^{\prime} = 0 \tag{2.10}$
我们发现(2.10)其实就是一个直线方程了，这个直线方程正是$p$的对极线，我们需要搜索的对应点$p^{\prime}$正是在对极线上。

---

去掉归一化坐标系的限制，引入基础矩阵

我们在本征矩阵那一节考虑的是归一化的坐标系，那么如果在原始的图像坐标系中，我们需要改写成：
$\begin{aligned}\mathbf{p} &= \mathcal{K} \mathbf{\hat{p}} \\\mathbf{p}^{\prime} &= \mathcal{K}^{\prime} \mathbf{\hat{p}}^{\prime}\end{aligned}\tag{2.11}$
其中，$\mathcal{K}, \mathcal{K}^{\prime}$是$3 \times 3$的标定矩阵，$\mathbf{\hat{p}}, \mathbf{\hat{p}}^{\prime}$是图像点的单位坐标向量。那么我们有：
$\mathbf{p}^{\mathrm{T}} \mathcal{F} \mathbf{p}^{\prime} = 0\tag{2.12}$
其中，矩阵$\mathcal{F} = \mathcal{K}^{-\mathrm{T}} \mathcal{E} {\mathcal{K}^{\prime}}^{-1}$称之为基础矩阵(Fundamental matrix)。

通常来说，无论是基础矩阵还是本征矩阵都可以通过内外参数的标定来求得，特别地，通过足够多的的图像匹配计算，我们同样可以无须采用标定图像，也可以得到这两个矩阵。

---

Reference

[1]. 电子科技大学自动化学院 杨路 老师 计算机视觉课程课件。

[2]. https://blog.csdn.net/LoseInVain/article/details/102632940

[3]. Hartley R, Zisserman A. Multiple View Geometry in Computer Vision[J]. Kybernetes, 2008, 30(9/10):1865 - 1872.

[4]. http://answers.opencv.org/question/83807/normalized-camera-image-coordinates/

[5]. http://answers.opencv.org/question/83807/normalized-camera-image-coordinates/

[6]. https://en.wikipedia.org/wiki/Cross_product