几何变换——关于透视变换和仿射变换以及齐次坐标系的讨论

几何变换——关于透视变换和仿射变换以及齐次坐标系的讨论

2019/10/26 FesianXu

前言

在本文首先介绍了引入齐次坐标系的必要性，随后介绍了在几何变换中常见的投射变换和仿射变换，这俩种变换在计算机视觉问题中，包括在相机成像过程中都是很基础并且重要的内容。
如有谬误，请联系指正。转载请注明出处。

$\nabla$ 联系方式：
e-mail: FesianXu@gmail.com
QQ: 973926198
github: https://github.com/FesianXu

---

文章目录

• 前言
• 齐次坐标系的引入
• 投影变换的背景
• 坐标表达
• 仿射变换和透视变换
• 仿射变换
• 尺度放缩(scale)
• 平移(translate)
• 切变(shear)
• 旋转（rotate）
• 可组合性
• 透视变换
• 广义投影变换
• Reference

齐次坐标系的引入

投影变换的背景

我们对于投影变换(projective transformation) 其实是一点的不陌生的，假设我们在看一张照片时，我们经常会发现本来应该是平行的线条，却变得不平行了，如Fig 1.1所示。更一般地说，在投影变换中，大部分的几何属性，比如长度，角度，比例，平行性等，都可能不能保留了，但是有一点我们是可以确保的，那就是 直线在变换前后始终还是直线。

Fig 1.1 本来应该是平行的马路，在相机成像的时候，则变成了“不平行”，汇聚于无限远处的消失点(vanishing point)。

Fig 1.2 现代的绘画作品很多采用了透视的方法增强了立体感，这是在仿照人类视觉的特点。

我们考虑到在欧式几何(Euclidean Geometry)中，其实有一些概念是有些“麻烦之处”的，比如说到平行这个概念，我们知道在欧几里德空间中，两个直线都会交于一点，当然除了平行线之外，这让平行线处于在一个很特殊的地位。如果我们熟悉编程我们就不难发现，当有个编程对象处于特殊地位时，我们就不得不单独考虑他，使得整个程序变得不能通用(general)起来，这个是个糟糕的事情。

当然，我们也可以耍滑头，说在欧几里德空间里，平行线相交于无限远的点处，这当然没问题。但是，“无限远”这种概念其实是为了方便定义出来的，实际上并不存在。不管怎么样，我们把平行线相交于的无限远的点，称之为 理想点(Ideal point)。

通过添加了这个理想点，我们把欧几里德空间(Euclidean Space)转变成了投影空间(Projective Space)，很简单吧，但是我们后面将会发现，我们的很多投影变换都只能在投影空间中进行，在没有定义出理想点的欧式空间，我们根本对这些变换无能为力。总而言之， 在投影空间中，所有的线最终都能够相交了。因为所有的理想点都有着相同的距离，所以在二维的投影空间中，所有的平行线其实都是交于由所有理想点组成的“理想直线”上的。同样的，在三维投影空间中，所有的平行面都交于一个“理想平面”。我们如果用符号$\mathbb{R}^{2}$表示二维的欧式空间，那么用$\mathbb{P}^{2}$表示二维的投影空间。

坐标表达

我们都知道一个在二维平面上的点可以用一组有序的二元对表示，如$(x,y)$。我们在此引入 齐次坐标(homogeneous coordinate) 的表达，我们将同样的二维点$(x,y)$表示成$(x,y,1)$，并且，其等价于$(kx, ky, k), k \neq 0$。 我们发现，基本上所有的齐次坐标表达$(x,y,c)$，都可以找到相对应的非齐次坐标表达方式$(x/c, y/c, 1)$，除了一个最为特殊的点$(x,y,0)$。这个点如果硬要用非齐次的方式去表示，那么只能表示为$(x/0, y/0, 1)$，我们发现，这个方式其实就是在齐次坐标系里面定义出了理想点这个概念，并且的，这个处于无限远处的理想点和普通点有着一致的表达方式，意味着可以用和普通点一样的处理方式去处理理想点这个概念了。

这个正是投影空间的精髓之处，在投影空间中，我们用齐次坐标去表示点，把空间中的点所有都看成是等价的，这样就不存在普通点与理想点的区别了，而且在这个空间中，所有的直线都会相交，因此也不存在平行性这个概念了。笔者在这里举个在投影空间处理点的变换的例子，假如现在在投影空间$\mathbb{P}^{n}$中定义了一个变换，我们首先用齐次坐标表示这个空间中的元素先，其是一个$(n+1)$维的向量，然后，我们定义这个变换，这个变换应该是一个矩阵，我们称之为单应性矩阵（homography），$\mathcal{H} \in \mathbb{R}^{(n+1) \times (n+1)}$，因此这个变换结果最后为:
$\mathbf{X}^{\prime} = \mathcal{H} \mathbf{X} \tag{1.1}$
通过这种方法，我们会发现我们同时可以考虑在欧式空间中的平行线和非平行线。这对处理投影变换非常的方便，因为投影变换是不保留平行性这个几何属性的，因此在变换的过程中，可能需要将平行线变换成非平行的。

---

仿射变换和透视变换

投影变换可以细分为 仿射变换(affine transform) 和 透视变换(perspective transform)，以及 广义的投影变换(general projective transform)。我们分别介绍下。
PS：注意，我们这里的点是二维点，也就是$\mathbf{x} = (u,v,1)^{\mathrm{T}} \in \mathbb{R}^3$，因此，单应性矩阵是$\mathcal{H} \in \mathbb{R}^{3 \times 3}$。如果延展到三维空间的点变换，那么点就是三维点，为$\mathbf{X} = (u,v,w,1)^{\mathrm{T}} \in \mathbb{R}^4$，单应性矩阵$\mathcal{H} \in \mathbb{R}^{4 \times 4}$。

仿射变换

仿射变换(affine transform)在变换前后，保留了元素的平行性，也就是说，在变换前是平行线的，在变换后同样也是平行线。仿射变换可以表示为一组线性变换，如(2.1)，同时，在齐次表达下，仿射变换通常可以用一个$2 \times 3$的矩阵表达（二维情况下），如(2.2)。
$\left[ \begin{matrix} x \\ y \end{matrix} \right] = \left[ \begin{matrix} a_{11} u + a_{12} v + a_{13} \\ a_{21} u + a_{22} v + a_{23} \end{matrix} \right] \tag{2.1}$

$\left[ \begin{matrix} x \\ y \\ 1 \end{matrix} \right] = \left[ \begin{matrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ 0 & 0 & 1 \end{matrix} \right] \left[ \begin{matrix} u \\ v \\ 1 \end{matrix} \right] \tag{2.2}$

通过对这六个元素的某些约束，比如令某些为0，为1等，我们将仿射变换又分成了以下若干种。

尺度放缩(scale)

尺度放缩(scale)的变换矩阵如：
$\mathcal{H} = \left[ \begin{matrix} a_{11} & 0 & 1\\ 0 & a_{22} & 0 \\ 0 & 0 & 1 \end{matrix} \right] \tag{2.3}$

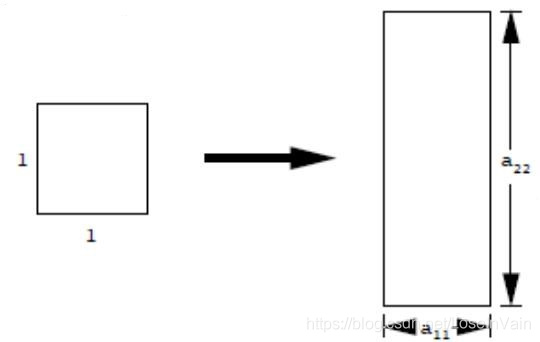
Fig 2.1 尺度放缩示意图。

平移(translate)

平移(translate)的变换矩阵如：
$\mathcal{H} = \left[ \begin{matrix} 1 & 0 & a_{13}\\ 0 & 1 & a_{23} \\ 0 & 0 & 1 \end{matrix} \right] \tag{2.4}$

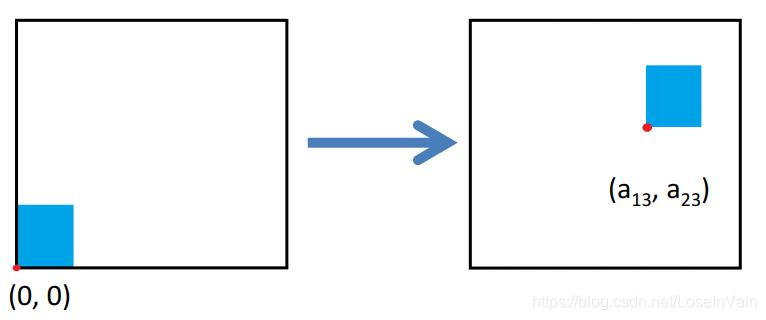
Fig 2.2 平移示意图。

切变(shear)

切变(shear)的变换矩阵如：
$\mathcal{H} = \left[ \begin{matrix} 1 & a_{12} & 0\\ a_{21} & 1 & 0 \\ 0 & 0 & 1 \end{matrix} \right] \tag{2.5}$

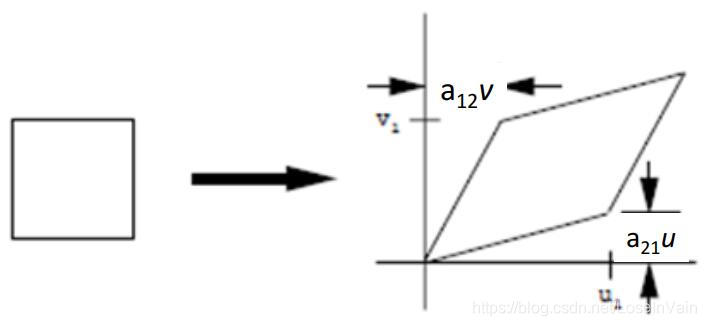
Fig 2.3 切变示意图。

旋转（rotate）

旋转(rotate)的变换矩阵如：
$\mathcal{H} = \left[ \begin{matrix} \cos(\theta) & -\sin(\theta) & 0\\ \sin(\theta) & \cos(\theta) & 0 \\ 0 & 0 & 1 \end{matrix} \right] \tag{2.6}$

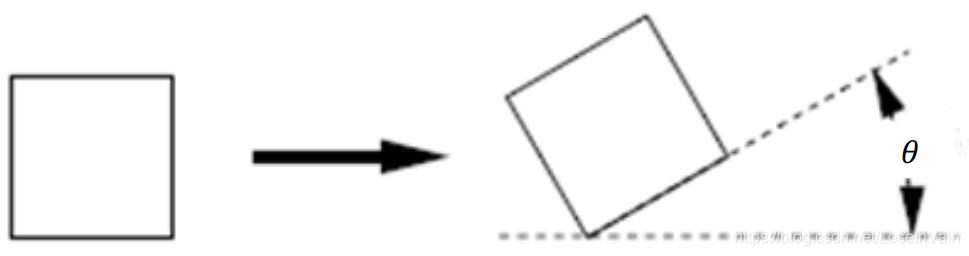
Fig 2.4 旋转示意图。

可组合性

注意到仿射变换其是可以组合的，比如一个变换可以是先平移，后旋转，最后放缩，那么其变换矩阵为:
$\mathcal{H} = \mathcal{S}((\mathcal{R}(\mathcal{T}\mathbf{X}))) \tag{2.7}$
其中$\mathcal{S}$代表放缩变换，$\mathcal{R}$代表旋转变换，$\mathcal{T}$代表平移变换。

但是，我们也要注意到，一般来说其是不具有交换性的，比如先平移在旋转一般结果和先旋转后平移是不同的，即是：
$\mathcal{T}\mathcal{R} \neq \mathcal{R}\mathcal{T} \tag{2.8}$
其本质是矩阵乘法的不可交换性。

透视变换

透视变换(perspective transform)在变换前后不再保留所有元素的平行性了，但是变换前后，直线还是保持是直线，使用这种变换能提供3D的视觉效果。

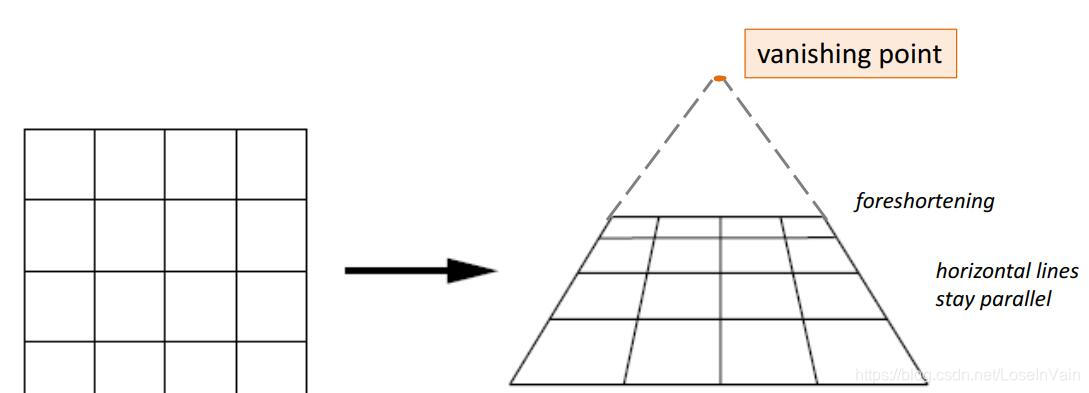
Fig 3.1 透视变换，不能保证保留所有的平行性。其原先的平行线可能相交于理想点，也就是图中的消失点(vanishing point)。

我们同样用齐次坐标去表示这个变换，其变换矩阵的形式如:
$\left[ \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ a_{31} & a_{32} & 1 \end{matrix} \right] \tag{3.1}$
观察变换过程(3.2)，我们发现本来在仿射变换中为1的$w$不再是1了。
$\left[ \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ a_{31} & a_{32} & 1 \end{matrix} \right] \left[ \begin{matrix} u \\ v \\ 1 \end{matrix} \right] = \left[ \begin{matrix} u \\ v \\ a_{31} u + a_{32} v + 1 = w \end{matrix} \right] \tag{3.2}$
将其表示为非齐次的形式，我们有：
$\left[ \begin{matrix} u/w \\ v/w \\ 1 \end{matrix} \right]$
我们发现其是一个非线性变换，因此，透视变换其是一个非线性变换，处于无限远处的点可能会被移到有限处，处于有限点也可能会被移到无限点处，正是因为如此，平行性才不能被保留了。

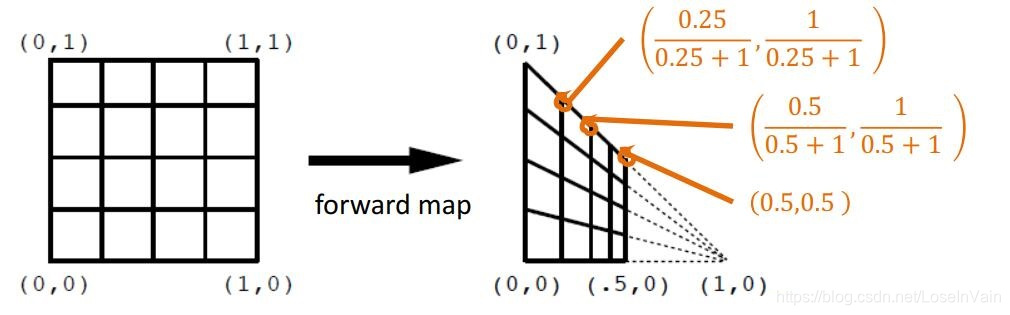
Fig 3.2 透视变换的例子。

我们这里举个例子，假设有个透视变换矩阵:

$\mathcal{H} = \left[ \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \end{matrix} \right]$
我们于是有转换过程:
$\mathcal{H} \left[ \begin{matrix} u \\ v \\ 1 \end{matrix} \right] = \left[ \begin{matrix} u \\ v \\ u+1 \end{matrix} \right] = \left[ \begin{matrix} \dfrac{u}{u+1} \\ \dfrac{v}{u+1} \\ 1 \end{matrix} \right] \tag{3.3}$
我们有:
$\begin{aligned} \lim_{u \rightarrow \infin} \dfrac{u}{u+1} &= 1 \\ \lim_{u \rightarrow \infin} \dfrac{v}{u+1} &= 0 \end{aligned} \tag{3.4}$
我们发现这个极限点正是其消失点的坐标。

广义投影变换

我们要注意到，透视变换其本质是广义的投影变换中的一种特殊情况，广义透视变换的变换矩阵如：
$\left[ \begin{matrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{matrix} \right] \tag{4.1}$

同样的，其也是一种非线性变换。在二维情况下我们有：
$\begin{aligned} x &= \dfrac{a_{11} u + a_{12} v + a_{13}}{a_{31} u + a_{32} v + a_{33}} \\ y &= \dfrac{a_{21} u + a_{22} v + a_{23}}{a_{31} u + a_{32} v + a_{33}} \end{aligned}$

---

Reference

[1]. Hartley R, Zisserman A. Multiple View Geometry in Computer Vision[J]. Kybernetes, 2008, 30(9/10):1865 - 1872.