通俗易懂的KMP算法详解

 

角色：

甲：abbaabbaaba
乙：abbaaba

乙对甲说：「帮忙找一下我在你的哪个位置。」

甲从头开始与乙一一比较，发现第 7 个字符不匹配。

要是在往常，甲会回退到自己的第 2 个字符，乙则回退到自己的开头，然后两人开始重新比较。^[1]这样的事情在字符串王国中每天都在上演：不匹配，回退，不匹配，回退，……

但总有一些妖艳字符串要花出自己不少的时间。

上了年纪的甲想做出一些改变。于是甲把乙叫走了：「你先一边玩去，我自己研究下。」

甲给自己定了个小目标：发生不匹配，自己不回退。

甲发现，若要成功与乙匹配，必须要匹配 7 个字符。也就是说，就算自己回退了，在后续的匹配流程中，肯定还要匹配自己的第 7 个字符。

当在甲的某个字符 c 上发生不匹配时，甲即使回退，最终还是会重新匹配到字符 c 上。

那干脆不回退，岂不美哉！

甲不回退，乙必须回退地尽可能少，并且乙回退位置的前面那段已经和甲匹配，这样甲才能不用回退。

如何找到乙回退的位置？

「不匹配发生时，前面匹配的那一小段 abbaab 于我俩是相同的」，甲想，「这样的话，用 abbaab 的头部去匹配 abbaab 的尾部，最长的那段就是答案。」

具体来说，
abbaab 的头部有 a, ab, abb, abba, abbaa（不包含最后一个字符。下文称之为「前缀」）
abbaab 的尾部有 b, ab, aab, baab, bbaab（不包含第一个字符。下文称之为「后缀」）
这样最长匹配是 ab，乙回退到第三个字符和甲继续匹配。

「要计算的内容只和乙有关」，甲想，「那就假设乙在所有位置上都发生了不匹配，乙在和我匹配之前把所有位置的最长匹配都算出来（算个长度就行），生成一张表，之后我俩发生不匹配时直接查这张表就行。」

据此，甲总结出了一条甲方规则：

所有要与甲匹配的字符串，必须先自身匹配：对每个子字符串 [0...i]，算出其「相匹配的前缀与后缀中，最长的字符串的长度」。

甲把乙叫了回来，告诉他新出炉的甲方规则。

「小 case，我对自己还不了解吗」，乙眨了一下眼睛，「那我回退到第三个字符和你继续匹配就行了」。

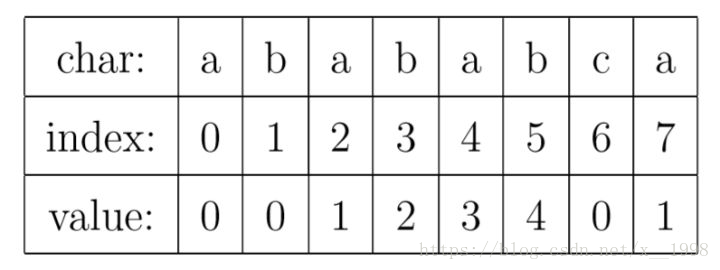
有些算法，适合从它产生的动机，如何设计与解决问题这样正向地去介绍。但KMP算法真的不适合这样去学。最好的办法是先搞清楚它所用的数据结构是什么，再搞清楚怎么用，最后为什么的问题就会有恍然大悟的感觉。我试着从这个思路再介绍一下。大家只需要记住一点，PMT是什么东西。然后自己临时推这个算法也是能推出来的，完全不需要死记硬背。KMP算法的核心，是一个被称为部分匹配表(Partial Match Table)的数组。我觉得理解KMP的最大障碍就是很多人在看了很多关于KMP的文章之后，仍然搞不懂PMT中的值代表了什么意思。这里我们抛开所有的枝枝蔓蔓，先来解释一下这个数据到底是什么。对于字符串“abababca”，它的PMT如下表所示：

 

就像例子中所示的，如果待匹配的模式字符串有8个字符，那么PMT就会有8个值。

我先解释一下字符串的前缀和后缀。如果字符串A和B，存在A=BS，其中S是任意的非空字符串，那就称B为A的前缀。例如，”Harry”的前缀包括{”H”, ”Ha”, ”Har”, ”Harr”}，我们把所有前缀组成的集合，称为字符串的前缀集合。同样可以定义后缀A=SB， 其中S是任意的非空字符串，那就称B为A的后缀，例如，”Potter”的后缀包括{”otter”, ”tter”, ”ter”, ”er”, ”r”}，然后把所有后缀组成的集合，称为字符串的后缀集合。要注意的是，字符串本身并不是自己的后缀。

有了这个定义，就可以说明PMT中的值的意义了。PMT中的值是字符串的前缀集合与后缀集合的交集中最长元素的长度。例如，对于”aba”，它的前缀集合为{”a”, ”ab”}，后缀 集合为{”ba”, ”a”}。两个集合的交集为{”a”}，那么长度最长的元素就是字符串”a”了，长 度为1，所以对于”aba”而言，它在PMT表中对应的值就是1。再比如，对于字符串”ababa”，它的前缀集合为{”a”, ”ab”, ”aba”, ”abab”}，它的后缀集合为{”baba”, ”aba”, ”ba”, ”a”}， 两个集合的交集为{”a”, ”aba”}，其中最长的元素为”aba”，长度为3。

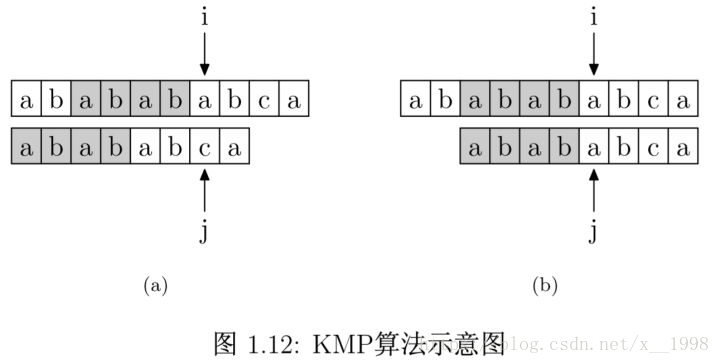
好了，解释清楚这个表是什么之后，我们再来看如何使用这个表来加速字符串的查找，以及这样用的道理是什么。如图 1.12 所示，要在主字符串"ababababca"中查找模式字符串"abababca"。如果在 j 处字符不匹配，那么由于前边所说的模式字符串 PMT 的性质，主字符串中 i 指针之前的 PMT[j −1] 位就一定与模式字符串的第 0 位至第 PMT[j−1] 位是相同的。这是因为主字符串在 i 位失配，也就意味着主字符串从 i−j 到 i 这一段是与模式字符串的 0 到 j 这一段是完全相同的。而我们上面也解释了，模式字符串从 0 到 j−1 ，在这个例子中就是”ababab”，其前缀集合与后缀集合的交集的最长元素为”abab”， 长度为4。所以就可以断言，主字符串中i指针之前的 4 位一定与模式字符串的第0位至第 4 位是相同的，即长度为 4 的后缀与前缀相同。这样一来，我们就可以将这些字符段的比较省略掉。具体的做法是，保持i指针不动，然后将j指针指向模式字符串的PMT[j −1]位即可。

简言之，以图中的例子来说，在 i 处失配，那么主字符串和模式字符串的前边6位就是相同的。又因为模式字符串的前6位，它的前4位前缀和后4位后缀是相同的，所以我们推知主字符串i之前的4位和模式字符串开头的4位是相同的。就是图中的灰色部分。那这部分就不用再比较了。

 

有了上面的思路，我们就可以使用PMT加速字符串的查找了。我们看到如果是在 j 位 失配，那么影响 j 指针回溯的位置的其实是第 j −1 位的 PMT 值，所以为了编程的方便， 我们不直接使用PMT数组，而是将PMT数组向后偏移一位。我们把新得到的这个数组称为next数组。下面给出根据next数组进行字符串匹配加速的字符串匹配程序。其中要注意的一个技巧是，在把PMT进行向右偏移时，第0位的值，我们将其设成了-1，这只是为了编程的方便，并没有其他的意义。在本节的例子中，next数组如下表所示。

 

// 返回值为首次匹配的串的第一个字符的下标
/* 
    不能写 while( i < t.length() && j < p.length() )，
    因为当j = -1时，因为p.length()是无符号整数，则-1 > p.length(),
    这样就产生了错误
    所以要事先用有符号整数保存 t.length()和p.length()的值
*/
int kmp(string t, string p)
{
    int i = 0, j = 0;

    int tlen = t.length();
    int plen = p.length();
    while (i < tlen && j < plen)
    {
        if (j == -1 || t[i] == p[j])
        {
            ++i;
            ++j;
        }
        else
        {
            j = nxt[j];
        }
    }

    if (j == plen)
        return i - j;
    else
        return -1;
}

 

好了，讲到这里，其实KMP算法的主体就已经讲解完了。你会发现，其实KMP算法的动机是很简单的，解决的方案也很简单。远没有很多教材和算法书里所讲的那么乱七八糟，只要搞明白了PMT的意义，其实整个算法都迎刃而解

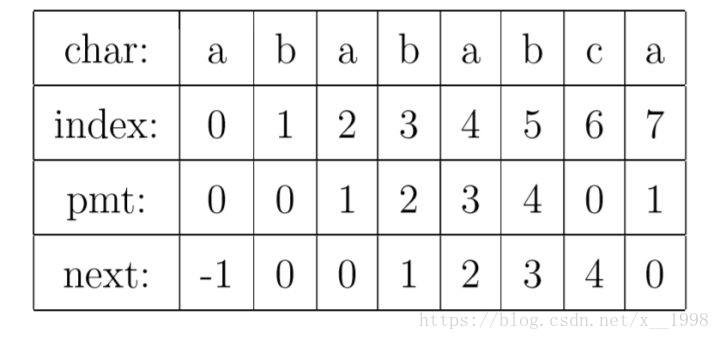
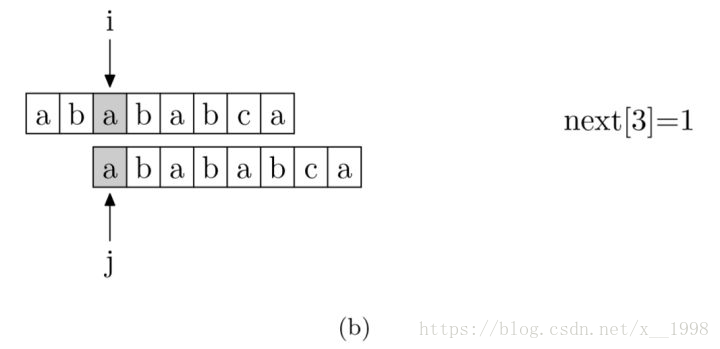
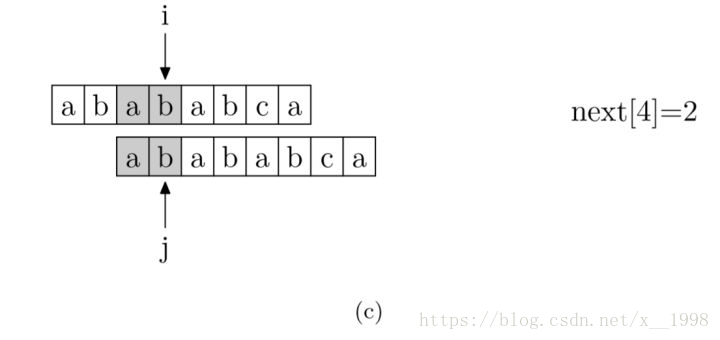
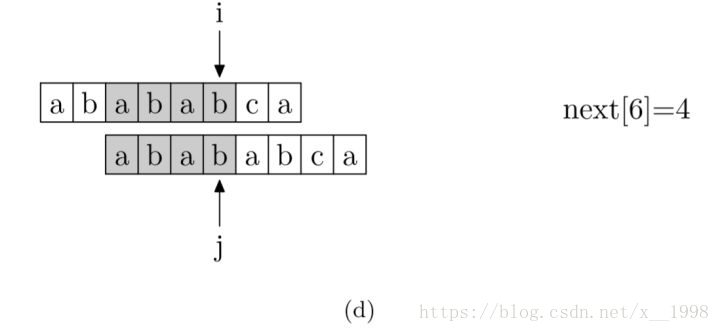
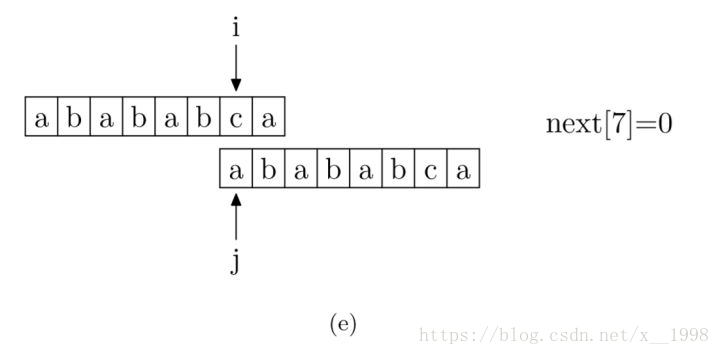
现在，我们再看一下如何编程快速求得next数组。其实，求next数组的过程完全可以看成字符串匹配的过程，即以模式字符串为主字符串，以模式字符串的前缀为目标字符串，一旦字符串匹配成功，那么当前的next值就是匹配成功的字符串的长度

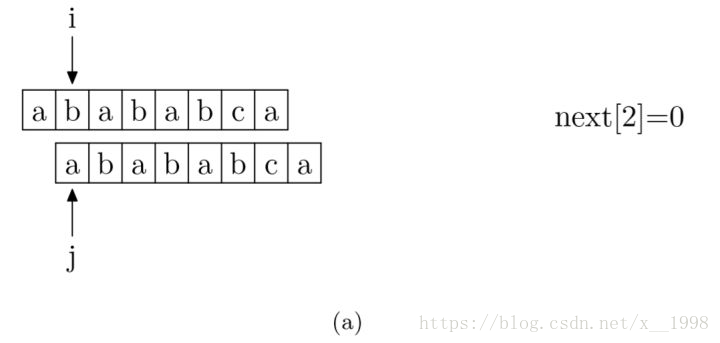
具体来说，就是从模式字符串的第一位(注意，不包括第0位)开始对自身进行匹配运算。 在任一位置，能匹配的最长长度就是当前位置的next值。如下图所示。

求next数组值的程序如下所示：

int nxt[1010];

// 已经有库函数叫做next，所以next数组的命名不能再叫做next，否则会报next不明确的错误，这里改为nxt
void getNext(string p, int nxt[])
{
    nxt[0] = -1;
    int i = 0, j = -1;
    
    int plen = p.length();
    while (i < plen)
    {
        if (j == -1 || p[i] == p[j])
        {
            ++i;
            ++j;
            nxt[i] = j;    // nxt[1]恒等于0 
        }
        else
        {
            j = nxt[j];
        }
    }
}

 

复杂度估计：

假设原串长度为n, 匹配串长度为m。我们可以看到，匹配串每次往前移动，都是一大段一大段移动，假设匹配串里不存在重复的前缀和后缀，即next的值都是-1，那么每次移动其实就是一整个匹配串往前移动m个距离。然后重新一一比较，这样就比较m次，概括为，移动m距离，比较m次，移到末尾，就是比较n次，O(n)复杂度。 假设匹配串里存在重复的前缀和后缀，我们移动的距离相对小了点，但是比较的次数也小了，整体代价也是O(n)。所以复杂度是一个线性的复杂度O(n)。同理，求next数组的复杂度为O(m)，总体就为O(m+n)。

 

 

作者：海纳

链接：https://www.zhihu.com/question/21923021/answer/281346746
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。