Loading

POJ 1222 EXTENDED LIGHTS OUT (熄灯问题)

Time Limit: 1000MS   Memory Limit: 10000K
Total Submissions: 8417   Accepted: 5441

Description

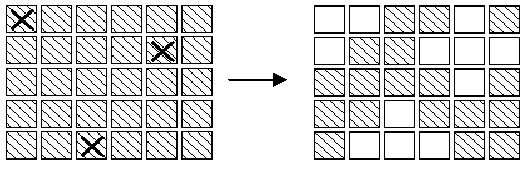
In an extended version of the game Lights Out, is a puzzle with 5 rows of 6 buttons each (the actual puzzle has 5 rows of 5 buttons each). Each button has a light. When a button is pressed, that button and each of its (up to four) neighbors above, below, right and left, has the state of its light reversed. (If on, the light is turned off; if off, the light is turned on.) Buttons in the corners change the state of 3 buttons; buttons on an edge change the state of 4 buttons and other buttons change the state of 5. For example, if the buttons marked X on the left below were to be pressed,the display would change to the image on the right. 

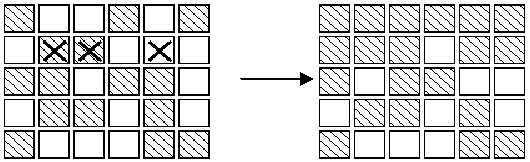
The aim of the game is, starting from any initial set of lights on in the display, to press buttons to get the display to a state where all lights are off. When adjacent buttons are pressed, the action of one button can undo the effect of another. For instance, in the display below, pressing buttons marked X in the left display results in the right display.Note that the buttons in row 2 column 3 and row 2 column 5 both change the state of the button in row 2 column 4,so that, in the end, its state is unchanged. 

Note: 
1. It does not matter what order the buttons are pressed. 
2. If a button is pressed a second time, it exactly cancels the effect of the first press, so no button ever need be pressed more than once. 
3. As illustrated in the second diagram, all the lights in the first row may be turned off, by pressing the corresponding buttons in the second row. By repeating this process in each row, all the lights in the first 
four rows may be turned out. Similarly, by pressing buttons in columns 2, 3 ?, all lights in the first 5 columns may be turned off. 
Write a program to solve the puzzle.

Input

The first line of the input is a positive integer n which is the number of puzzles that follow. Each puzzle will be five lines, each of which has six 0 or 1 separated by one or more spaces. A 0 indicates that the light is off, while a 1 indicates that the light is on initially.

Output

For each puzzle, the output consists of a line with the string: "PUZZLE #m", where m is the index of the puzzle in the input file. Following that line, is a puzzle-like display (in the same format as the input) . In this case, 1's indicate buttons that must be pressed to solve the puzzle, while 0 indicate buttons, which are not pressed. There should be exactly one space between each 0 or 1 in the output puzzle-like display.

Sample Input

2
0 1 1 0 1 0
1 0 0 1 1 1
0 0 1 0 0 1
1 0 0 1 0 1
0 1 1 1 0 0
0 0 1 0 1 0
1 0 1 0 1 1
0 0 1 0 1 1
1 0 1 1 0 0
0 1 0 1 0 0

Sample Output

PUZZLE #1
1 0 1 0 0 1
1 1 0 1 0 1
0 0 1 0 1 1
1 0 0 1 0 0
0 1 0 0 0 0
PUZZLE #2
1 0 0 1 1 1
1 1 0 0 0 0
0 0 0 1 0 0
1 1 0 1 0 1
1 0 1 1 0 1

 

 

　　所以，枚举第一行按钮是否按下的所有状态就行。

 

解法一： 使用for循环枚举（只适用于循环层数已知的情况）

  1 #include<iostream>
  2 #include<cstring>
  3 #include<stdio.h>　
  4 
  5 using namespace std;
  6 
  7 int n; 
  8 int p = 1;
  9 int orig_maze[5][6];    //原始的迷宫
 10 int maze[5][6];            //每次循环后都要将maze重新还原为orig_maze
 11 int result[5][6] = { 0 };
 12 
 13 void opposite(int x, int y)
 14 {
 15     if (x >= 0 && x < 5 && y >= 0 && y < 6)
 16     {
 17         if (maze[x][y] == 0)
 18             maze[x][y] = 1;
 19         else
 20             maze[x][y] = 0;
 21     }
 22 }
 23 
 24 void press(int x, int y)
 25 {
 26     opposite(x, y);
 27     opposite(x + 1, y);
 28     opposite(x - 1, y);
 29     opposite(x, y + 1);
 30     opposite(x, y - 1);
 31 }
 32 
 33 bool judge()
 34 {
 35     for (int i = 0; i < 5; ++i)
 36         for (int j = 0; j < 6; ++j)
 37         {
 38             if (maze[i][j] == 1)
 39                 return false;
 40         }
 41     return true;
 42 
 43 
 44 }
 45 
 46 void solve()
 47 {
 48     for (int i = 0; i < 5; ++i)
 49         for (int j = 0; j < 6; ++j)
 50         {
 51             cin >> orig_maze[i][j];
 52             maze[i][j] = orig_maze[i][j];
 53         }
 54 
 55     //枚举第一行按下的按钮
 56     for (result[0][0] = 0; result[0][0] <= 1; result[0][0]++)
 57         for (result[0][1] = 0; result[0][1] <= 1; result[0][1]++)
 58             for (result[0][2] = 0; result[0][2] <= 1; result[0][2]++)
 59                 for (result[0][3] = 0; result[0][3] <= 1; result[0][3]++)
 60                     for (result[0][4] = 0; result[0][4] <= 1; result[0][4]++)
 61                         for (result[0][5] = 0; result[0][5] <= 1; result[0][5]++)
 62                         {
 63                             for (int i = 0; i <= 5; ++i)
 64                             {    //按第一行    
 65                                 if (result[0][i] == 1)
 66                                     press(0, i);
 67                             }
 68 
 69                             //由第一行算出后面四行
 70                             for (int i = 1; i <= 4; ++i)
 71                             {
 72                                 int k = i - 1;    //k表示i的上一行
 73                                 for (int j = 0; j <= 5; ++j)
 74                                 {
 75                                     if (maze[k][j] == 1)
 76                                     {
 77                                         result[i][j] = 1;   //将其置为1表示按下
 78                                         press(i, j);
 79                                     }
 80                                     else
 81                                         result[i][j] = 0;    //没按下一定要置零，因为以前循环时置的1还保留在此
 82                                 }
 83                             }
 84 
 85                             if (judge() == true)
 86                             {
 87                                 printf("PUZZLE #%d\n", p++);
 88                                 for (int i = 0; i < 5; ++i)
 89                                 {
 90                                     int j;
 91                                     for (j = 0; j < 5; ++j)
 92                                         cout << result[i][j] << ' ';
 93                                     cout << result[i][j] << endl;
 94                         
 95                                 }
 96                                 return ;
 97                             }
 98 
 99                             memcpy(maze, orig_maze, sizeof(orig_maze));    //将迷宫还原
100                         }
101 }
102 
103 
104 int main()
105 {
106     int n;
107     cin >> n;
108     
109     while (n--)
110     {
111         solve();
112     }
113 
114 
115     return 0;
116 }

 

解法二： 使用dfs枚举（适用于循环层数未知的情况）

  1 #include<iostream>
  2 #include<cstring>
  3 #include<stdio.h>　
  4 
  5 using namespace std;
  6 
  7 int m, n;
  8 int orig_maze[20][20];    //原始的迷宫
  9 int maze[20][20];        //每次循环后都要将maze重新还原为orig_maze
 10 int result[20][20] = { 0 };
 11 int book[1000000][20];    // 使用book保存第一行的所有枚举情况
 12 int index = 0;
 13 int p = 1;
 14 
 15 void opposite(int x, int y)
 16 {
 17     if (x >= 0 && x < m && y >= 0 && y < n)
 18     {
 19         if (maze[x][y] == 0)
 20             maze[x][y] = 1;
 21         else
 22             maze[x][y] = 0;
 23     }
 24 }
 25 
 26 void press(int x, int y)
 27 {
 28     opposite(x, y);
 29     opposite(x + 1, y);
 30     opposite(x - 1, y);
 31     opposite(x, y + 1);
 32     opposite(x, y - 1);
 33 }
 34 
 35 bool judge()
 36 {
 37     for (int i = 0; i < m; ++i)
 38         for (int j = 0; j < n; ++j)
 39         {
 40             if (maze[i][j] == 1)
 41                 return false;
 42         }
 43     return true;
 44 
 45 
 46 }
 47 
 48 void dfs(int step)
 49 {
 50     if (step == n)
 51     {
 52         for (int i = 0; i < n; ++i)
 53             book[index][i] = result[0][i];    // 使用book保存第一行的所有枚举情况
 54         index++;
 55         return;
 56     }
 57 
 58     for (int i = 0; i <= 1; ++i)
 59     {
 60         result[0][step] = i;
 61         dfs(step + 1);
 62     }
 63 }
 64 
 65 void g()
 66 {
 67 
 68     for (int i = 0; i < m; ++i)
 69         for (int j = 0; j < n; ++j)
 70         {
 71             cin >> orig_maze[i][j];
 72             maze[i][j] = orig_maze[i][j];
 73         }
 74 
 75     dfs(0);
 76 
 77     for (int t = 0; t < index; ++t)
 78     {
 79         for (int t1 = 0; t1 < n; ++t1)
 80         {
 81             result[0][t1] = book[t][t1];
 82         }
 83 
 84         for (int i = 0; i < n; ++i)
 85         {    //按第一行
 86             if (result[0][i] == 1)
 87                 press(0, i);
 88         }
 89 
 90         //由第一行算出后面m-1行
 91         for (int i = 1; i < m; ++i)
 92         {
 93             int k = i - 1;    //k表示i的上一行
 94             for (int j = 0; j < n; ++j)
 95             {
 96                 if (maze[k][j] == 1)
 97                 {
 98                     result[i][j] = 1;   //将其置为1表示按下
 99                     press(i, j);
100                 }
101                 else
102                     result[i][j] = 0;    //没按下一定要置零，因为以前循环时置的1还保留在此
103             }
104         }
105 
106         if (judge() == true)
107         {
108             printf("PUZZLE #%d\n", p++);
109             for (int i = 0; i < m; ++i)
110             {
111                 int j;
112                 for (j = 0; j < n - 1; ++j)
113                     cout << result[i][j] << ' ';
114                 cout << result[i][j] << endl;
115 
116             }
117             return ;
118         }
119         memcpy(maze, orig_maze, sizeof(orig_maze));    //将迷宫还原
120     }
121 
122 }
123 
124 int main()
125 {
126     m = 5;
127     n = 6;
128     int k;
129     cin >> k;
130     while(k--)
131     {
132         g();
133     }
134 
135 
136 
137     return 0;
138 }

 

posted @ 2019-03-11 13:45  拾月凄辰  阅读(269)  评论(0)  编辑  收藏  举报