计数排序

输入数组A长度为n，数据范围为m1~m2。

建立一个长度m2-m1+1的数组B用做临时数组。

1.统计A中每个数字出现的次数，记录在B中。B[i]=k：A中值为i的索引一共有k处。

2.统计比A中每个数字小的数字个数，也就是统计A中每个数字应该在最终数组中排到的位置。

3.开一个结果数组C，倒序从A[n-1]到A[0]依次放入结果数组相应位置。

比如：原数组：1、2、1、3、5

统计数组B：0、0、0、0、0

经过第1步，B为：2、1、1、0、1。（2个1，1个2，1个3，0个4，1个5）

经过第2步，B为：2、3、4、4、5。

第3步：A[4]=5，B[5-1]=5：所以C[4]=5，B[5-1]=4。

最终填好结果数组C

代码：

void CountingSort(vector<int>& nums){
    int n=nums.size();
    if(n==0){return;}
    int minVal=INT32_MAX,maxVal=INT32_MIN;
    for(const int& x:nums){
        minVal=min(minVal,x);
        maxVal=max(maxVal,x);
    }
    int k=maxVal-minVal;  //数据范围
    vector<int> tmp(k+1,0);
    for(const int& x:nums){ //第1步
        tmp[x-minVal]++;
    }
    for(int i=1;i<tmp.size();++i){//第2步
        tmp[i]+=tmp[i-1];
    }
    vector<int> res(n,0);
    for(int i=n-1;i>=0;--i){　　
        res[tmp[nums[i]-minVal]-1]=nums[i];
        tmp[nums[i]-minVal]--;
    }
    for(int x:res){
        cout<<x<<" ";
    }
}

 

关键点：如果不要求稳定性，可以不做第2、3步，完成第1步之后就直接从小到大将数字填入结果数组。

考虑A：1、2、1

如果不做2、3步，顺序遍历的话，无法保证稳定性，因为两个1不知道哪个在前哪个在后了。

解释：（来自：https://www.cnblogs.com/kyoner/p/10604781.html）

给出一个学生的成绩表，要求按成绩从底到高排序，如果成绩相同，则遵循原表固有顺序。

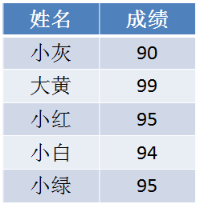
当我们填充统计数组之后，我们只知道有两个成绩并列95分的学生，却不知道谁是小红，谁是小绿：

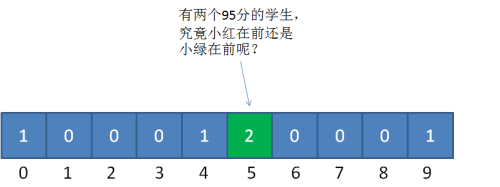
对此，我们只需在填充完统计数组之后，对统计数组做一下变形。我们仍然以学生的成绩表为例，把之前的统计数组进行变形，统计数组从第二个元素开始，每一个元素都加上前面所有元素之和：

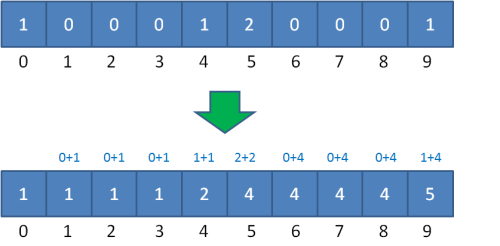
相加的目的就是为了让统计数组存储的元素值等于相应整数的最终排序位置。比如下标是9的元素值是5，代表原始数列的整数9最终的排序是在第5位。

接下来，我们创建输出数组sortedArray，长度和输入数列一致，然后从后向前遍历输入数列：

第一步，遍历成绩表最后一行的小绿：小绿是95分，找到countArray下标为5的元素，值是4，代表小绿的成绩排名是在第4位。

同时给countArray下标是5的元素值减1，从4变成3，代表着下次再遇到95分时，最终排名是第3位。

第二步，遍历成绩表倒数第二行的小白：小白是94分，找到countArray下标是4的元素，值是2，代表小白的成绩排名在第2位。

同时，给countArray下标是4的元素值减1，从2变成1，代表下次再遇到94分的成绩时（实际上已经遇不到了），最终排名是第1位。

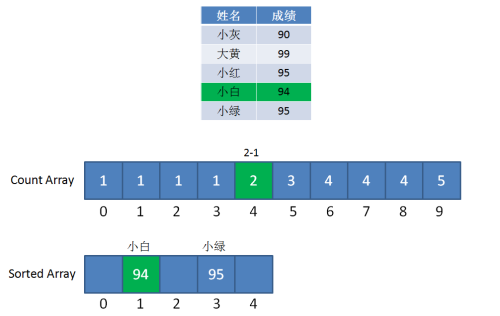
第三步，遍历成绩表倒数第三行的小红：小红是95分，找到countArray下标是5的元素，值是3（最初是4，减1变成了3），代表小白的成绩排名在第3位。

同时，给countArray下标是5的元素值减1，从3变成2，代表下次再遇到95分的成绩时（实际上已经遇不到了），最终排名是第2位。

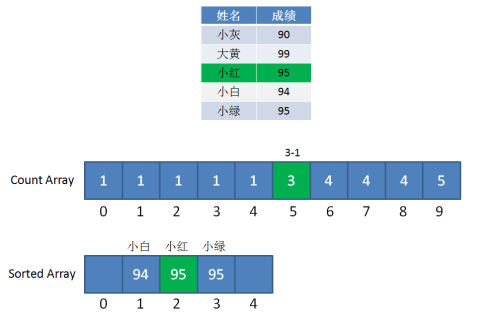
因此，同样是95分的小红和小绿就能清楚地排出顺序，所以优化版的计数排序属于稳定排序。

后面的遍历过程依此类推。