474. 一和零

题目：

在计算机界中，我们总是追求用有限的资源获取最大的收益。

现在，假设你分别支配着 m 个 0 和 n 个 1。另外，还有一个仅包含 0 和 1 字符串的数组。

你的任务是使用给定的 m 个 0 和 n 个 1 ，找到能拼出存在于数组中的字符串的最大数量。每个 0 和 1 至多被使用一次。

注意:

给定 0 和 1 的数量都不会超过 100。
给定字符串数组的长度不会超过 600。
示例 1:

输入: Array = {"10", "0001", "111001", "1", "0"}, m = 5, n = 3
输出: 4

解释: 总共 4 个字符串可以通过 5 个 0 和 3 个 1 拼出，即 "10","0001","1","0" 。
示例 2:

输入: Array = {"10", "0", "1"}, m = 1, n = 1
输出: 2

解释: 你可以拼出 "10"，但之后就没有剩余数字了。更好的选择是拼出 "0" 和 "1" 。

 

解答：

三维dp：

dp[i][j][k]表示：前i个字符串，用j个0和k个1一共最多可以拼出多少个字符串（小于等于i）。

dp[i][j][k]要么等于dp[i-1][j][k]：即第i个字符串我不看了，和之前i-1个字符串用j个0、k个1的结果一样就行了。

要么拼出第i个字符串，则该字符串要使用x个0和y个1。那么dp[i][j][k]=dp[i-1][j-x][k-y]：截止前i-1个字符串、使用j-x个0、k-y个1的结果。

二者取较大者。

class Solution {
public:
    pair<int,int> calculate(const string& str){
        pair<int,int> res={0,0};
        for(const char& c:str){
            if(c=='0'){
                res.first+=1;
            }
            else{
                res.second+=1;
            }
        }
        return res;
    }
    int findMaxForm(vector<string>& strs, int m, int n) {
        int dp[601][101][101]={0};
        int strCnt=strs.size();
        for(int seq=1;seq<=strCnt;++seq){
            for(int i=0;i<=m;++i){
                for(int j=0;j<=n;++j){
                    dp[seq][i][j]=dp[seq-1][i][j];
                    auto pair=calculate(strs[seq-1]);
                    if(i>=pair.first and j>=pair.second){
                        dp[seq][i][j]=max(dp[seq][i][j],dp[seq-1][i-pair.first][j-pair.second]+1);
                    }
                }
            }
        }
        return dp[strCnt][m][n];
    }
};

 

 

然后发现dp第i层时只用到第i-1层的数据，那么可以利用滚动数组来压缩空间，缩减为二维dp：

class Solution {
public:
    pair<int,int> calculate(const string& str){
        pair<int,int> res={0,0};
        for(const char& c:str){
            if(c=='0'){
                res.first+=1;
            }
            else{
                res.second+=1;
            }
        }
        return res;
    }
    int findMaxForm(vector<string>& strs, int m, int n) {
        int dp[101][101]={0};
        int strCnt=strs.size();
        pair<int,int> pair={0,0};
        for(int seq=1;seq<=strCnt;++seq){
            for(int i=m;i>=0;--i){
                for(int j=n;j>=0;--j){
                    pair=calculate(strs[seq-1]);
                    if(i>=pair.first and j>=pair.second){
                        dp[i][j]=max(dp[i][j],dp[i-pair.first][j-pair.second]+1);
                    }
                }
            }
        }
        return dp[m][n];
    }
};

 

 好像没多大变化。。

然后我发现我在每次最内层嵌套的循环里计算的当前字符串str[i]的0、1个数，一个一样的结果算了101*101遍。。

就是这里：

 

 

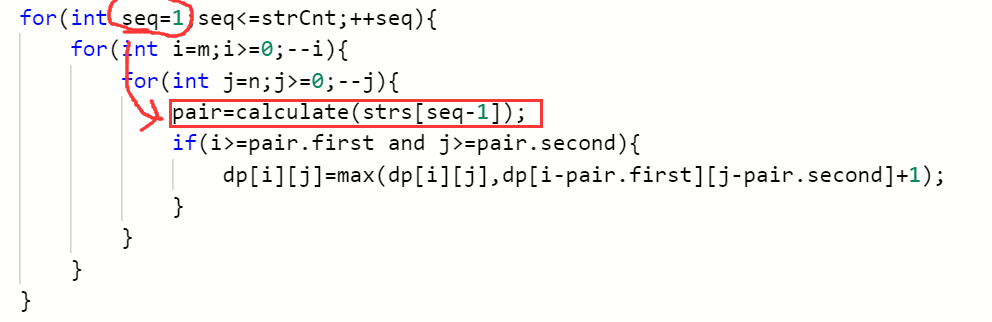
赶紧优化一下，顺便用二维数组来替代pair：

class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        int dp[101][101]={0};
        int strCnt=strs.size();
        for(int seq=1;seq<=strCnt;++seq){
            int p[2]={0};
            for(const char& c:strs[seq-1]){
                if(c=='0'){
                    p[0]+=1;
                }
                else{
                    p[1]+=1;
                }
            }
            for(int i=m;i>=p[0];--i){
                for(int j=n;j>=p[1];--j){
                    dp[i][j]=max(dp[i][j],dp[i-p[0]][j-p[1]]+1);
                }
            }
        }
        return dp[m][n];
    }
};

 

 完美！