1162. 地图分析

题目：

你现在手里有一份大小为 N x N 的『地图』（网格） grid，上面的每个『区域』（单元格）都用 0 和 1 标记好了。其中 0 代表海洋，1 代表陆地，你知道距离陆地区域最远的海洋区域是是哪一个吗？请返回该海洋区域到离它最近的陆地区域的距离。

我们这里说的距离是『曼哈顿距离』（ Manhattan Distance）：(x0, y0) 和 (x1, y1) 这两个区域之间的距离是 |x0 - x1| + |y0 - y1| 。

如果我们的地图上只有陆地或者海洋，请返回 -1。

 

示例 1：

 

输入：[[1,0,1],[0,0,0],[1,0,1]]
输出：2
解释：
海洋区域 (1, 1) 和所有陆地区域之间的距离都达到最大，最大距离为 2。
示例 2：

 

输入：[[1,0,0],[0,0,0],[0,0,0]]
输出：4
解释：
海洋区域 (2, 2) 和所有陆地区域之间的距离都达到最大，最大距离为 4。
 

提示：

1 <= grid.length == grid[0].length <= 100
grid[i][j] 不是 0 就是 1

 

解答：

(x1,y1)到(x2,y2)的曼哈顿距离其实可以理解为从(x1,y1)bfs到达(x2,y2)的步数（反过来也行）。

题目要求距离陆地区域最远的海洋区域是是哪一个？返回该海洋区域到离它最近的陆地区域的距离。翻译一下：对于每个海洋(i,j)，它到所有陆地的距离为(dis1,dis2,dis3...)，其中最小值为dis k。则该值dis k就是该海洋(i,j)到离它最近的陆地区域的距离。

对于所有的海洋，我们要求解每个海洋对应的dis k，最终取所有这些dis k中最大的那个。 

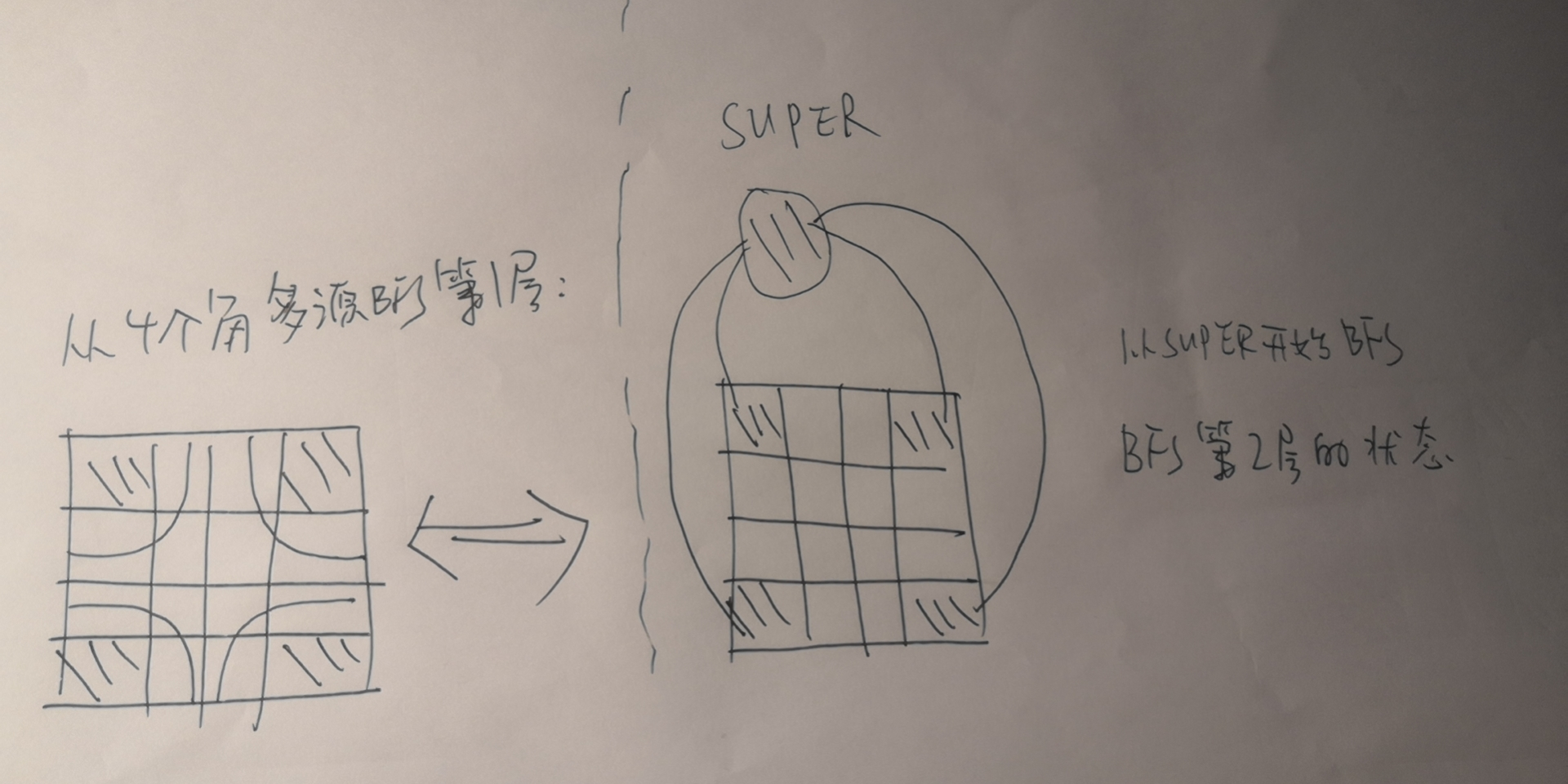
我们不需要从每个海洋开始bfs遍历整个图，只需要从每个陆地开始多源bfs遍历即可，直到覆盖了全部海洋。

 

 

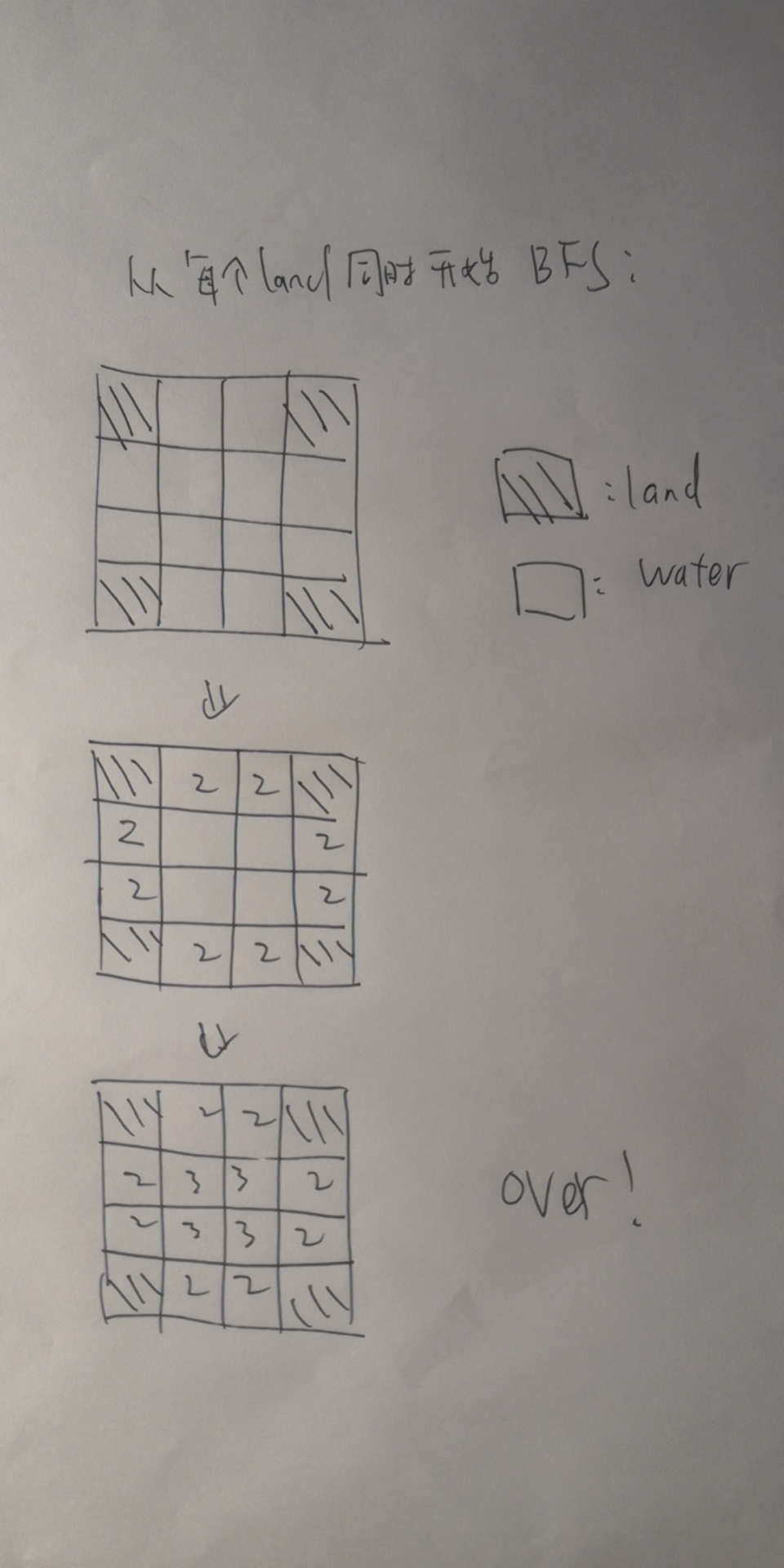
多源bfs第一层的状态其实就是从另一个超级源点开始bfs的第二层时候的状态：

 

 

class Solution {
public:
    int maxDistance(vector<vector<int>>& grid) {
        int step=1;
        bool flag=true;
        vector<vector<int>> dif={{0,1},{0,-1},{-1,0},{1,0}};
        int rows=grid.size(),cols=grid[0].size();
        while(flag){
            flag=false;
            for(int i=0;i<rows;++i){
                for(int j=0;j<cols;++j){
                    if(grid[i][j]==step){
                        for(int k=0;k<4;++k){
                            if(i+dif[k][0]>=0 and i+dif[k][0]<rows and j+dif[k][1]>=0 and j+dif[k][1]<cols and grid[i+dif[k][0]][j+dif[k][1]]==0){          
　　　　　　　　　　　　　　　　　　　grid[i+dif[k][0]][j+dif[k][1]]=step+1;    
                            　　flag=true;
                            }
                        }
                    }
                }
            }
            // for(auto& row:grid){
            //     for(int x:row){
            //         cout<<x<<" ";
            //     }cout<<endl;
            // }cout<<"---------"<<endl;
            ++step;
        }
        int res=0;
        for(int i=0;i<rows;++i){
            for(int j=0;j<cols;++j){
                if(grid[i][j]>1){
                    res=max(res,grid[i][j]);
                }
            }
        }
        return res?res-1:-1;
    }
};