C++实现索引堆及完整测试代码
首先贴一篇我看的博客,写的很清楚。作者:Emma_U
一些解释
索引堆首先是堆,但比堆肯定是更有用。
用处:
1.加速。 索引堆存储的是索引,并不直接存储值。在堆上浮下沉的元素交换的时候,交换索引可比交换值来的快。虽然我代码只实现了int类型的索引堆,但比方说string类型的索引堆,交换两个string,显然没有交换两个int型的索引快。
2.方便改动原数组 比如现在有一个vector,然后我们把它初始化为普通的堆,然后我们突然想改动vector中的第i个元素并恢复堆性质。但我们怎么找这个值在哪呢,毕竟堆只有首元素是可以在O(1)时间访问的。我们只有一个个遍历去寻找,这样时间是O(N),N是堆规模。但索引堆可以做到O(1)时间寻找并更新。虽然寻找并更新后重新恢复堆性质二者都需要O(logN)时间,但对于较大的N,二者的总体时间复杂度一个是O(N),一个是O(logN)。
稍微讲一下原理,因为我也是看文首的那篇博客学习的,也相当于复习了。首先我们声明一个data数组作为我们的原始数据集,除非人为更新其中的值,不然是不变的。data_size为data数组的规模。
另外就是我们堆的主体,一个index数组,大小等于data_size。其中的值初始化为0、1、2、3…data_size-1。也就是data数组所有元素的索引(此时还没初始化堆,所以是顺序的)。之后我们建堆后,data数组是不变的,我们只对index进行改动。最终我们对于index要保持这样的性质:data[index[i]]>data[index[2i+1]] and data[index[i]]>data[index[2i+2]]。 最终的结果就是:如果把index数组的每个元素值index[i]都作为索引改成data[index[i]],那index就是堆,这部分应该蛮好理解的。但到目前为止,我们如果更改data中的某个值,仍然要到index数组中一个个查找哪个是被改的,时间还是O(N),没有优化。目前所做的工作只是提高了建堆、维护堆性质等操作的时间开销,也就是只做了上面优点1的优化,优点2并没有实现。
下面是我觉得很不好理解的部分,怎么O(1)时间查询data数组中的第i个值。这里推荐去看文首的博客,我自我感觉不会讲的比作者更好。我下面针对那篇博客的内容补充一个证明,请先阅读那篇博客,一定要先看,不然你不知道我下面在证明什么!!!
下面的1~5编号的代码在我文后贴的index_heap.cpp中。下面证明map数组的值按照我的代码这样设置是正确的。
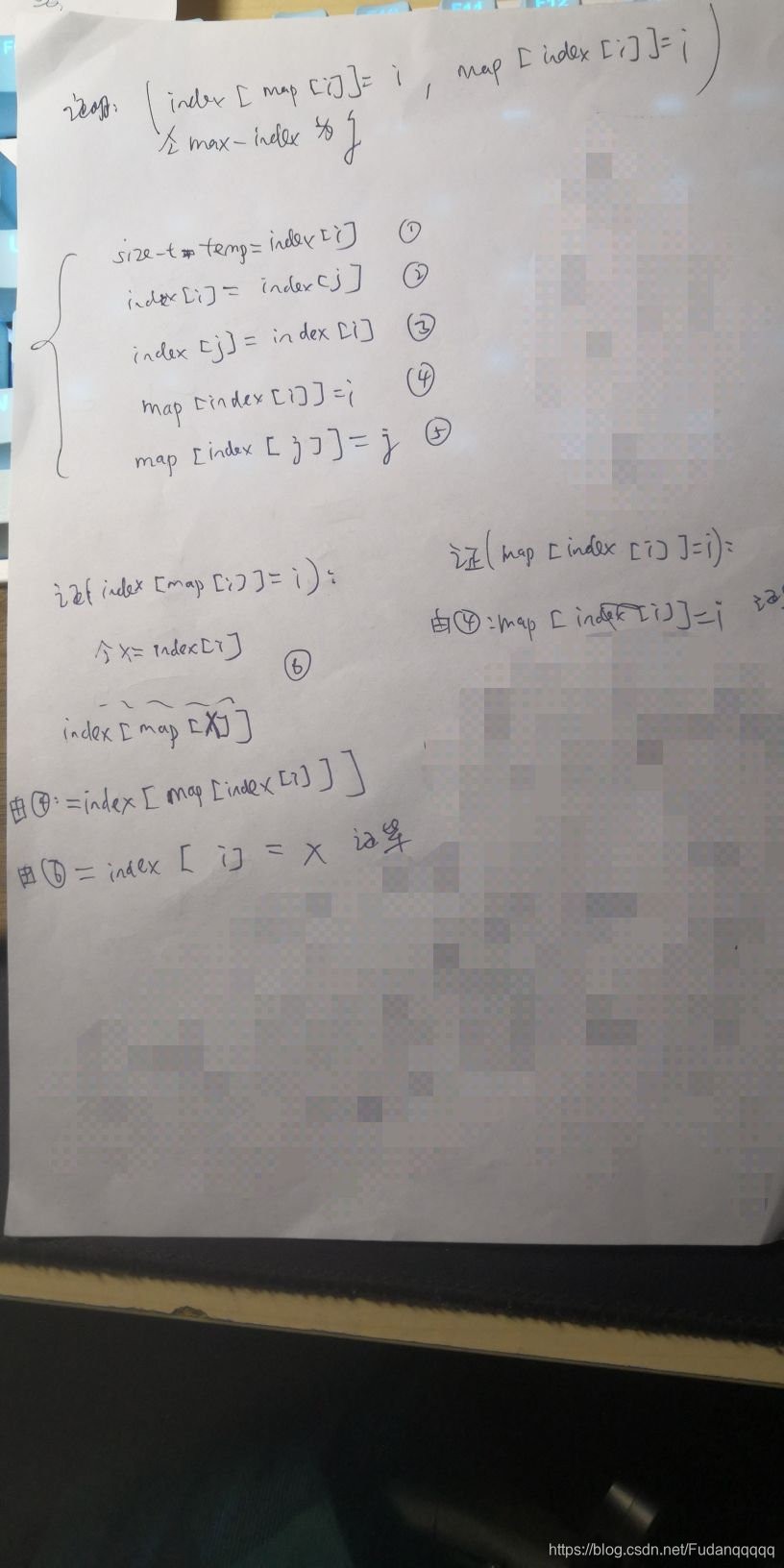
实现代码:
index_heap.h:
#pragma once
// #pragma warning(disable:4996)
#ifndef _INDEX_HEAP_H_
#define _INDEX_HEAP_H_
#include<iostream>
#include<vector>
using std::vector;
using std::cout;
using std::endl;
class index_heap {
vector<int> data; //数据数组
vector<int> index; //堆,index中存的是data中的索引,不存具体元素
vector<int> map; //映射,map[i]为data中索引i的元素在堆中的索引
int data_size;
public:
index_heap() :data_size(0) {}
~index_heap() {}
index_heap(const vector<int>&);
void create_max_heap();
void print();
void shift_down(size_t);
void shift_up(size_t);
void push(int);
void pop();
int top();
void change(size_t, int);
};
#endif
index_heap.cpp
#include"index_heap.h"
index_heap::index_heap(const vector<int>& vec) {
data = vec;
data_size = vec.size();
index.resize(data_size);
for (int i = 0; i < data_size; ++i) {
index[i] = i;
}
map = index;
create_max_heap();
}
void index_heap::create_max_heap() {
for (int i = data_size / 2 - 1; i >= 0; --i) {
shift_down(i);
}
}
void index_heap::print() {
if (data_size == 0) {
cout << "No data!" << endl;
return;
}
cout << "DATA:" << endl;
for (int num : data) {
cout << num << " ";
}
cout << endl << "INDEX:" << endl;
for (int num : index) {
cout << num << " ";
}
cout << endl << "MAP:" << endl;
for (int num : map) {
cout << num << " ";
}
}
//下沉
void index_heap::shift_down(size_t i) {
if (i >= data_size - 1) {
return;
}
int j = i;
if (2 * i + 1 < data_size and data[index[2 * i + 1]] > data[index[j]]) {
j = 2 * i + 1;
}
if (2 * i + 2 < data_size and data[index[2 * i + 2]] > data[index[j]]) {
j = 2 * i + 2;
}
if (i != j) {
int temp = index[i];
index[i] = index[j];
index[j] = temp;
map[index[i]] = i;
map[index[j]] = j;
shift_down(j);
}
}
//上浮
void index_heap::shift_up(size_t i) {
if (i >= data_size or i == 0) {
return;
}
size_t i_parent = i / 2 - 1; //i_parent是i的父亲节点
if (data[index[i_parent]] < data[index[i]]) {
int temp = index[i];
index[i] = index[i_parent];
index[i_parent] = temp;
map[index[i]] = i;
map[index[i_parent]] = i_parent;
shift_up(i_parent);
}
}
void index_heap::push(int x) {
data.push_back(x);
++data_size;
index.push_back(data_size - 1);
map.push_back(data_size - 1);
shift_up(data_size - 1);
}
void index_heap::pop() {
if (data_size == 0) {
cout << "No data can be popped!" << endl;
return;
}
size_t p = index[0];
data.erase(data.begin() + p);
index[0] = index[data_size - 1];//最后一个元素(即最小的元素)拿到堆顶
--data_size; //相当于删除了堆顶
index.resize(data_size);
map.resize(data_size);
map[index[0]] = 0;
shift_down(0); //恢复大顶堆性质
}
int index_heap::top() {
if (data_size == 0) {
cout << "No data can be topped!" << endl;
return INT_MAX;
}
return data[index[0]];
}
void index_heap::change(size_t i, int num) {
if (i >= data_size) {
cout << "Invalid index!" << endl;
return;
}
if (data[i] == num) {
cout << "Same number,no need to change!" << endl;
return;
}
int original_num = data[i];
data[i] = num;
if (original_num > num) {
shift_down(map[i]);
}
else {
shift_up(map[i]);
}
}
main.cpp(测试):
#include"index_heap.h"
int main()
{
vector<int> p = { 15,17,19,13,22,16,28,30,41,62};
index_heap heap(p);
heap.print();
getchar();
return 0;
}
我的运行截图:
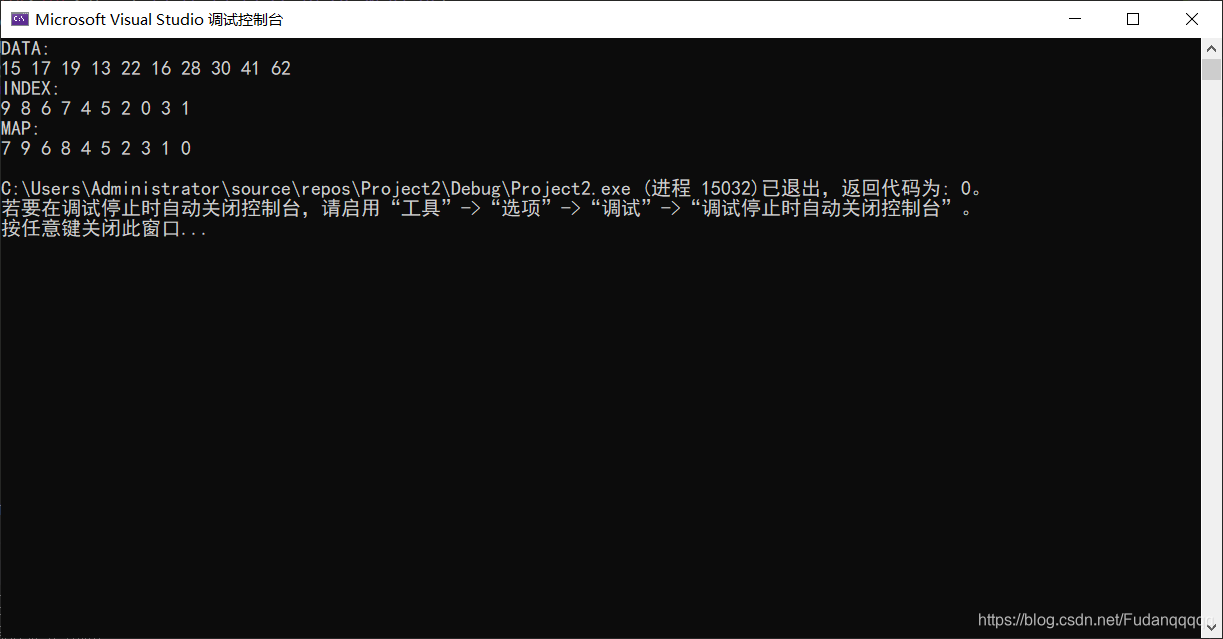
话说之前根本没听过索引堆这个名词,昨天做leetcode一道双端队列题时候看见这个名词,于是从昨天晚上看到今天下午,搞懂了一个新东西,还蛮有意思的哈。
2019年11月15日 16:05:44


 浙公网安备 33010602011771号
浙公网安备 33010602011771号