<Re:从零开始的算法总结>（1）--动态规划问题

判断动态规划问题

1. 动态规划问题的一般形式是求最值，比如最长递增序列、最小编辑距离等等
2. 求解动态规划的核心问题是穷举。求最值就是把所有的可行答案穷举出来，然后在里面找最值。
3. 求解动态规划的难点在于重叠子问题、最优子结构和状态转移方程

重叠子问题

什么是子问题

子问题是和原问题相似，但规模较小的问题。动态规划问题往往可以利用规模较小的问题的解得到规模较大的问题的解，且这个子问题往往是参数化的，是由某个参数（往往是问题规模和输入）决定的。

子问题应该具有两个性质:

1. 原问题要能由子问题表示。例如这道小偷问题中，k=nk=n 时实际上就是原问题。否则，解了半天子问题还是解不出原问题，那子问题岂不是白解了。
2. 一个子问题的解要能通过其他子问题的解求出。例如这道小偷问题中，f(k)可以由 f(k-1)和 f(k-2)求出，具体原理后面会解释。这个性质就是教科书中所说的最优子结构。如果定义不出这样的子问题，那么这道题实际上没法用动态规划解。

什么是重叠子问题

比如在已知10个班每个班的最高分和最低分求所有班级的最高分最低分，我们可以只比较每个班的最高最低分，这种情况下没有重叠子问题，而如果我们知道的是10个班的最高分最低分的分差，求所有班级的最高分最低分分差，就不能简单地比较这10个差值的最大值，因为可能最高分在a而最低分在b，此时我们获得的基本量之间存在重叠，就有了重叠子问题。

此时，如果想简单穷举得出，往往需要大量不必要的计算，甚至发生组合爆炸、指数爆炸。

如何在动态规划问题中处理重叠子问题

1. 动态规划问题一定会具备最优子结构，此时我们可以合理构造不重叠的子问题或者虽然有重叠但是不需要重复计算的子问题的最值来得到原问题的最值。

2. 如何利用我们找到的最优子结构的最值得到整体的最值就需要状态转移方程。状态转移方程是清晰地表示出规模较大的问题是如何根据已经处理好的规模较小的问题得出结果的，其当然可以通过自顶向下的递归完成，但是更加常用自底向上的动态生成数组得到，前者往往更加符合直觉思维，但是后者往往有更高的效率、更小的空间复杂度

   这里简单介绍寻找状态转移方程的思路：

   明确 base case -> 明确「状态」-> 明确「选择」 -> 定义 dp 数组/函数的含义。

   用python伪码得到

   # 初始化 base case
   dp[0][0][...] = base
   # 进行状态转移
   for 状态1 in 状态1的所有取值：
       for 状态2 in 状态2的所有取值：
           for ...
               dp[状态1][状态2][...] = 求最值(选择1，选择2...)
   

重叠子问题的一个基本例子

斐波那契数列（注:不是动态规划，因为它不求最值）

在多次递归中，产生大量重复计算，想要计算原问题 f(20)，我就得先计算出子问题 f(19) 和 f(18)，然后要计算 f(19)，我就要先算出子问题 f(18) 和 f(17)，以此类推。最后遇到 f(1) 或者 f(2) 的时候，结果已知，就能直接返回结果，递归树不再向下生长了。

这类算法的时间复杂度就是子问题个数乘以解决一个子问题需要的时间，显然本次算法共有2^n各子问题，每个子问题是O(1),所以是指数复杂度。

本算法的一种优化算法是

最优子结构

在递归的基础上优化

承接上面的斐波那契数列，一种优化算法是带备忘录的递归解法，既然耗时的原因是重复计算，那么我们可以造一个「备忘录」，每次算出某个子问题的答案后别急着返回，先记到「备忘录」里再返回；每次遇到一个子问题先去「备忘录」里查一查，如果发现之前已经解决过这个问题了，直接把答案拿出来用，不要再耗时去计算了。

一般使用一个数组充当这个「备忘录」，当然也可以使用哈希表（字典），思想都是一样的。

此时输出时，只需要查备忘录即可，求f(20)直接查备忘录的第二十个值（或者key为20的字典）即可，复杂度为O(1)。此时我们的最优子结构就是这个数组的元素或者字典的一条记录。

采用动态分配的思路

有了上一步「备忘录」的启发，我们可以把这个「备忘录」独立出来成为一张表，称作dp table。

之前对递归的优化仍然是自顶向下的，利用dp table可以从最简单的问题开始，逐步生成复杂问题的解。这时我们的最优子结构就是dp table内的一个元素。这种算法不采用递归，而是采用循环迭代，大部分情况下，与优化递归的效率基本相同。

状态转移方程

以斐波那契数列为例，它的转移方程就是

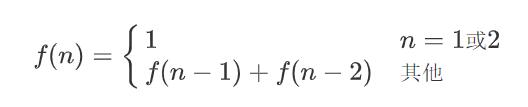
它表示对一个较大的问题规模（n），我们总能通过这个问题的子问题n-1和n-2解决，并且有确定的base case能够给定初值。

其实状态转移方程的最难点恰恰是写出暴力解，此后使用dp table进行优化即可。

进一步的优化（空间优化）

一般情况下，对动态分配问题的优化在于空间优化。

空间优化的基本原理是，很多时候我们不需要持有全部的dp数组，因此可以使用一定的技巧。这个技巧就是所谓的「状态压缩」，如果我们发现每次状态转移只需要 DP table 中的一部分，那么可以尝试用状态压缩来缩小 DP table 的大小，只记录必要的数据，上述例子就相当于把DP table 的大小从 n 缩小到 2。后续的动态规划章节中我们还会看到这样的例子，一般来说是把一个二维的 DP table 压缩成一维，即把空间复杂度从 O(n^2) 压缩到 O(n)。

每个解需要用到之前固定个数的子问题解的情况，往往使用滚动数组求解，即递推时保留有限个邻近的子问题，并不断用规模大的问题覆盖规模小的问题。

根据斐波那契数列的状态转移方程，只需要知道与之相关的前两个状态即可，并且由于动态分配自底向上的优点，我们完全可以仅仅借助两个位置创建整个dp table。

参考资料1-知乎大佬的解答

参考资料2-leetcode的解析