POJ1486 Sorting Slides
POJ1486 Sorting Slides
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 2246 | Accepted: 822 |
Description
Professor Clumsey is going to give an important talk this afternoon. Unfortunately, he is not a very tidy person and has put all his transparencies on one big heap. Before giving the talk, he has to sort the slides. Being a kind of minimalist, he wants to do this with the minimum amount of work possible.
The situation is like this. The slides all have numbers written on them according to their order in the talk. Since the slides lie on each other and are transparent, one cannot see on which slide each number is written.
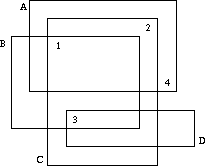
Well, one cannot see on which slide a number is written, but one may deduce which numbers are written on which slides. If we label the slides which characters A, B, C, ... as in the figure above, it is obvious that D has number 3, B has number 1, C number 2 and A number 4.
Your task, should you choose to accept it, is to write a program that automates this process.
The situation is like this. The slides all have numbers written on them according to their order in the talk. Since the slides lie on each other and are transparent, one cannot see on which slide each number is written.

Well, one cannot see on which slide a number is written, but one may deduce which numbers are written on which slides. If we label the slides which characters A, B, C, ... as in the figure above, it is obvious that D has number 3, B has number 1, C number 2 and A number 4.
Your task, should you choose to accept it, is to write a program that automates this process.
Input
The input consists of several heap descriptions. Each heap descriptions starts with a line containing a single integer n, the number of slides in the heap. The following n lines contain four integers xmin, xmax, ymin and ymax, each, the bounding coordinates of the slides. The slides will be labeled as A, B, C, ... in the order of the input.
This is followed by n lines containing two integers each, the x- and y-coordinates of the n numbers printed on the slides. The first coordinate pair will be for number 1, the next pair for 2, etc. No number will lie on a slide boundary.
The input is terminated by a heap description starting with n = 0, which should not be processed.
This is followed by n lines containing two integers each, the x- and y-coordinates of the n numbers printed on the slides. The first coordinate pair will be for number 1, the next pair for 2, etc. No number will lie on a slide boundary.
The input is terminated by a heap description starting with n = 0, which should not be processed.
Output
For each heap description in the input first output its number. Then print a series of all the slides whose numbers can be uniquely determined from the input. Order the pairs by their letter identifier.
If no matchings can be determined from the input, just print the word none on a line by itself.
Output a blank line after each test case.
If no matchings can be determined from the input, just print the word none on a line by itself.
Output a blank line after each test case.
Sample Input
4 6 22 10 20 4 18 6 16 8 20 2 18 10 24 4 8 9 15 19 17 11 7 21 11 2 0 2 0 2 0 2 0 2 1 1 1 1 0
Sample Output
Heap 1 (A,4) (B,1) (C,2) (D,3) Heap 2 none
Source
******************************************************************************
题目大意: 这道题的意思是一些大小不等透明的幻灯片(只有轮廓和上面的数字可见)A、B、C、D、E…按顺序叠放在一起,现在知道每个幻灯片左上角和右下角的坐标,并且由于幻灯片是透明的,所以能看到幻灯片上的数字(给出了每个数字的坐标,但不知道这些数字分别属于哪个幻灯片),现在要你根据当前的已知信息,输出能够确定的幻灯片编号和数字的匹配,例如(A,4) (B,1) (C,2) (D,3); 解题思路:网上常说什么二分图的必须边,需要先匈牙利一遍再一一删边求答案。但个人觉得没必要,这题一看,第一眼:贪心。我每次贪一个维度为1的点,然后把他的对应点找出来,然后将与对应点相连的点的维度都减去1.然后继续贪心。
#include <stdio.h>
#include <string.h>
#include <vector>
#define N 60
using namespace std;
vector<int>gra[N];
int dis[N],vis[N];
int da[N][4],n,mat[N];
void re(void)
{
for(int i=1;i<=2*n;i++)
gra[i].clear();
memset(dis,0,sizeof(dis));
for(int i=1;i<=n;i++)
scanf("%d%d%d%d",&da[i][0],&da[i][1],&da[i][2],&da[i][3]);
for(int i=1;i<=n;i++)
{
int x,y;
scanf("%d%d",&x,&y);
for(int j=1;j<=n;j++)
if((x>da[j][0]&&x<da[j][1])&&(y>da[j][2]&&y<da[j][3]))
{
gra[i+n].push_back(j);
gra[j].push_back(i+n);
dis[i+n]++;
dis[j]++;
}
}
}
void run(int s)
{
memset(vis,0,sizeof(vis));
memset(mat,0,sizeof(mat));
for(int h=1;h<=n;h++)
{
int pos;
for(pos=1;pos<=2*n;pos++)
if(!vis[pos]&&dis[pos]==1)
break;
if(pos>2*n)
{
break;
}
vis[pos]=1;
int opp;
for(int i=0;i<gra[pos].size();i++)
if(!vis[gra[pos][i]])
{
opp=gra[pos][i];
break;
}
vis[opp]=1;
for(int i=0;i<gra[opp].size();i++)
dis[gra[opp][i]]--;
if(opp<pos)
{
int temp=pos;
pos=opp;opp=temp;
}
mat[pos]=opp;
}
int flag=0;
printf("Heap %d\n",s);
for(int i=1;i<=n;i++)
{
if(mat[i]<n)continue;
if(flag)printf(" ");
printf("(%c,%d)",i-1+'A',mat[i]-n);
flag++;
}
if(!flag)
printf("none");
puts("\n");
}
int main()
{
int h=1;
while(scanf("%d",&n),n)
{
re();
run(h++);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号