牛顿迭代法求解平方根

假设现在输入一个整数，希望通过某种方式来求得该整数的平方根，要求得到尽可能大的精度。

和 LeetCode 上的原题 LeetCode 69 不同，这里要求得到尽可能大的精度，因此一般的二分法无法处理这个问题

处理思路

考虑定义一个函数 $f(x) = x ^ 2 - a$，那么当 $f(x)$ 为 $0$ 时，所对应的正 $x$ 坐标就是 $a$ 的平方根。现在，在 $f(x)$ 上的任意一点，做出 $f(x)$ 处对应的切线，此时的横坐标为 $x_i$，这条切线和 $X$ 轴的交点的横坐标为 $x_{i + 1}$，具体如下图所示：

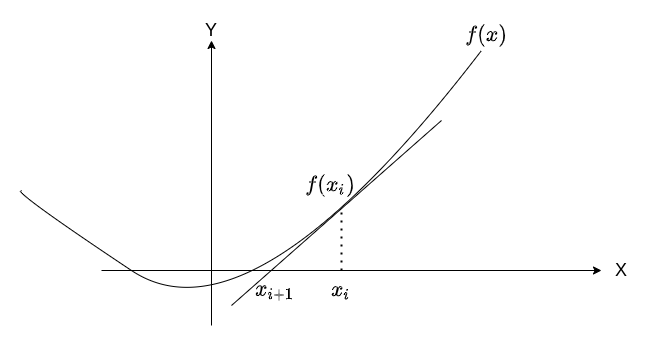
由于在 $f(x)$ 处的切线的斜率为当前位置的 $f(x)$ 的倒数，因此有如下的关系：

$$f(x_i) / (x_i - x_{i + 1}) = f'(x_i)$$

将该关系进行转换，可以得到 $x_{i + 1}$ 和 $x_i$ 之间的对应关系：

$$x_{i + 1} = x_i - f(x_i) / f'(x_i)$$

由于 $f(x) = x^2 - a$，由求导公式可得 $f'(x) = 2x$，将其带入上述的公式可得：

$$\begin{aligned} x_{i + 1} &= x_i - (x_i^2 - a) / 2x_i \\ &=x_i - x_i / 2 + a / 2x_i\\ &=(x_i + a/x_i) / 2 \end{aligned}$$

当 $x_i$ 非常接近 $\sqrt a$ 时，则有如下的对应关系：

$$x_{i + 1} = (\sqrt a + \sqrt a) / 2 = \sqrt a$$

即经过不断地迭代，最终结果收敛于 $\sqrt a$

编码实现

public static double sqrt(int n) {
    int ub = 20; //  20 次左右的迭代可以解决 32 位有符号整数的平方根
    double y = 0.5 * n; // 初始值默认为 0.5 倍的 n，如果能够取得更好的初始值，算法性能会有进一步的提升
    double rootx = Math.sqrt(n); // 实际平方根，用于比较
    for (int i = 0; i < ub; ++i) {
        System.out.printf("%05d: %25.16f %25.16f\n", i, y, Math.abs(y - rootx) / rootx);
        double newy = 0.5*(y + (double) n / y); // 迭代
        if (newy == y) {
            System.out.println("Converged");
            break;
        }
        y = newy;
    }

    return y;
}

时间复杂度：可以看到，如果有一个合适的初始值，牛顿迭代法可以是一个常数时间内的操作，即 $O(1)$

空间复杂度：只需要少量的几个中间变量，因此空间复杂度为 $O(1)$

参考：

^[1] 《编程珠矶（续）》Jon Bentley 第 14 章 编写数值计算程序