位运算（一）数组中数字出现的次数 Ⅱ
问题描述
在一个数组 \(nums\) 中，有一个数字只出现了一次，但是其它的数字都出现了三次，请找出那个只出现了一次的数字
说明：
-
数组的长度 \(n\) 满足 \(1\leq n \leq 1000\)
-
数组中每个元素的数据范围 \(1 \leq nums[i] \leq 2^{31}\)
解决思路
-
HashMap
通过
HashMap统计每个元素的出现次数，最后再遍历所有的 \(key\) 即可 -
位运算
由于每个元素都是 \(32\) 位的正整数，因此可以考虑通过位运算的方式来统计每个位上 \(1\) 的出现次数，由于多余的元素都出现了三次，那么只要该位出现 \(1\) 的次数不能被 \(3\) 整除，则说明该位确实是目标元素持有的 \(bit\) 位，执行 \(|\) 操作即可
-
有限自动机
对于一个整数的每个 \(bit\) ，进行遍历的过程中存在以下三种状态：对 \(3\) 取余为 \(0\)、\(1\)、\(2\) 三种情况。
考虑如下的状态转换：
-
如果当前处理位的值为 \(1\)，则会按照如下的状态机进行转换
-
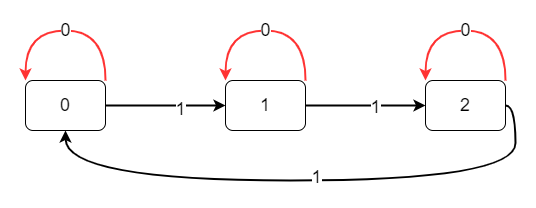
如果处理的位的值为 \(0\)，那么状态不会发生改变
为了维护这个状态的变化，一般情况下回考虑通过构建图的方式来构造这个状态机，但是在这里可以通过引入两个整形变量结合为运算来维护状态的变化。
具体地，引入两个整形变量 \(a\) 和 \(b\)，其中 \(a\) 表示在 \(0\) 位的状态值，而 \(b\) 则表示在 \(1\) 位的状态值，具体如下图所示：
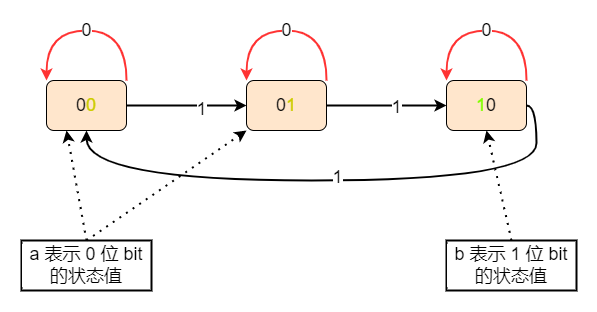
对于 \(a\) 的计算，伪代码如下：
if (b == 0): if (n == 0): a = a else if (n == 1): a = ~a else if (b == 1): a = 0其中，\(n\) 表示当前处理的 \(bit\) 位对应的值，如果引入异或运算，可以转换为：
if (b == 0): a ^= n else if (b == 1): a = 0继续引入与运算，可以转换为：
a = a ^ n & ~b对于 \(b\) 的计算：
由于是首先计算 \(a\) ，因此需要在 \(a\) 的基础上计算 \(b\)，和计算 \(a\) 的过程类似，最终计算 \(b\) 的方式为：
b = b ^ n & ~a -
对于每个元素的每一个位都可以按照如上的方式进行处理，最终 \(a\) 即为需要寻找的目标元素（表示每个位的有效值）
实现
-
HashMap
class Solution { public int singleNumber(int[] nums) { Map<Integer, Integer> map = new HashMap<>(); for (int val : nums) map.put(val, map.getOrDefault(val, 0) + 1); for (int key : map.keySet()) if (map.get(key) == 1) return key; return -1; } }复杂度分析：
-
时间复杂度：\(O(n)\)
-
空间复杂度：\(O(n)\)
-
-
位运算
class Solution { public int singleNumber(int[] nums) { int[] bits = new int[32]; for (int val : nums) { for (int i = 0; i < 31; ++i) { if (((val >> i) & 1) == 1) bits[i]++; } } int ans = 0; for (int i = 0; i < bits.length; ++i) { if (bits[i] % 3 == 0) continue; ans |= (1 << i); } return ans; } }复杂度分析：
-
时间复杂度：O(n)
-
空间复杂度：O(1)
-
-
有限自动机
class Solution { public int singleNumber(int[] nums) { int a = 0, b = 0; for(int num : nums){ a = a ^ num & ~b; b = b ^ num & ~a; } return a; } }复杂度分析：
-
时间复杂度：O(n)
-
空间复杂度：O(1)
-
参考：
