递归（一）二叉树的最近公共祖先
问题描述
给定一个二叉树，找到该树中两个指定节点的最近公共节点。
例如，对于给定的二叉树：
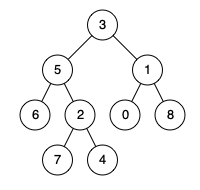
现在需要查找节点 \(2\) 和 \(0\) 的公共祖先节点，应当返回节点 \(3\)。
说明：
-
在输入的二叉树中，所有的节点值都是唯一的
-
要查找的节点 \(p\) 和 \(q\) 均存在于给定的二叉树中
解决思路
思路比较简单，只要遍历整个二叉树，然后检查正在遍历的节点是否同时包含 \(p\) 和 \(q\)，由于约束条件的存在，因此第一个同时包含 \(p\) 和 \(q\) 的节点必定是 \(p\) 和 \(q\) 两个节点的最近公共祖先
这里比较麻烦的地方在于情况的分析，如下：
-
如果当前遍历的节点的 \(left\) 和 \(right\) 都不包含 \(p\) 和 \(q\)，那么说明这两个节点不存在于当前节点的左右子树中，这种情况下应该返回 \(null\)
-
如果当前遍历的节点的 \(left\) 和 \(right\) 都含有一个待搜索的节点，那么说明 \(p\) 和 \(q\) 分布在当前遍历的节点的左右两侧，这种情况下当前的节点就是 \(p\) 和 \(q\) 的最近公共祖先节点
-
如果当前遍历的节点的 \(left\) 不包含 \(p\) 和 \(q\) 的任意一个节点，但是 \(right\) 至少包含 \(p\) 和 \(q\) 的一个节点，那么这种情况下需要进一步分析
-
\(p\) 和 \(q\) 的其中一个节点在 \(right\) 子树中，那么说明当前遍历的节点中包含 \(p\) 或 \(q\)
-
\(p\) 和 \(q\) 两个节点都在 \(right\) 子树中，那么此时的 \(right\) 节点就是 \(p\)、\(q\) 两个节点的最近公共祖先
-
当 \(left\) 不为空，但是 \(right\) 为空时，和第三种情况类似
实现
具体实现代码如下：
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) { val = x; }
}
class Solution {
public TreeNode lowestCommonAncestor(
TreeNode root, TreeNode p, TreeNode q
) {
// 递归的终止条件
if (root == null || root.val == p.val || root.val == q.val)
return root;
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
if (left == null && right == null) return null; // 对应第一种情况
if (left == null) return right; // 对应第三种情况
if (right == null) return left; // 对应第四种情况
return root; // 对应第二种情况
}
}
复杂度分析：
-
时间复杂度：由于需要遍历节点，在最差的情况下需要遍历所有的节点，因此时间复杂度为 \(O(n)\)
-
空间复杂度：忽略由于递归带来的栈空间消耗，空间复杂度为 \(O(1)\)
参考：
[1] https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-tree/
