B 树和 B+ 树及其实现

B 树

B 树和一般的二叉树有许多相似的地方，二者都是为了加快查找的速度，不同之处在于 B 树是为了解决大量的数据而产生的，更加适合读取相对大的数据块的存储系统。B 树的每个节点一般不会存储实际的数据，而只是存储对应的索引位置（类似指针）

B 树有时也被称作是 B- 树，这是为了和 B+ 树有一个区分。当描述一颗 B 树时，需要指定它的阶数 \(M\)，将该阶数的 B 树称为 \(M\) 阶 B 树

一颗 \(M\) 阶 B 树需要满足以下几个条件：

• 每个节点最多含有 \(M - 1\) 对键和链接
• 除根节点外， 每个节点最少含有 \(M / 2\) 对键和链接
• 包括根节点在内的所有节点至少含有 \(2\) 对键和链接

例如，假设现在有一棵阶数 \(M = 6\)​ 的 B 树，它看起来可能像下面这样：

[1]

实际上，B 树并不要求在节点中保存子树节点的副本，上图之所以会出现副本是因为它的实际使用情况导致的，具体可以查看 《算法（第四版）》中的细节

基本操作

• 查找

  B 树的查找是在可能含有被查找键的唯一子树中进行递归搜索，当且仅当被查找的键包含在当前的节点中时，每次的查找便会结束于一个外部节点。

  以下面的例子为例，假设现在想要查找键为 \(E\)​ 的数据，首先从根节点开始，按照所在区间查找子树，然后在子树中进行递归查找，最终，当查找叶子节点的时候，如果此时的叶子节点中存在对应的 \(E\)​ 节点，则读取这个节点对应的数据

  ^[1]

  
  

• 插入

  B 树的插入方式和 2-3 树的插入方式类似，当插入的数据所在的节点的键值对数未达到 \(M - 1\) 时，将会直接将数据节点插入到叶子节点；当插入数据元素使得节点的键值对数达到 \(M - 1\) 时，会使得当前的节点的键值对数短暂地 “溢出”，当递归调用结束之后再分裂当前的节点

  如下图所示：

  

  ^[1]

  
  

• 删除

  删除的操作比添加要复杂一些，为了简化这个问题，首先我们假设 B 树的阶数 \(M\) 只能是奇数

  删除 \(key\) 时可能会有两种情况：

  1. 删除的 \(key\)​​ 所在的节点是叶子节点

     这种情况下首先找到要删除的 \(key\)​，将它删除，然后调整节点使得所有的节点符合 B 树的定义

  2. 删除的 \(key\)​ 所在的节点是非叶子节点

     这种情况下，该 \(key\)​​​ 所在的节点的每个元素都是两个子树的分割节点，因此需要重新设置当前所在的 \(key\)，使得该节点依旧是符合要求的，具体做法如下：

     • 选择一个新的分隔元素（当前元素的左子树的最大节点或右子树的最小节点），将它从后继节点中删除，然后移动到当前元素的位置
     • 由于删除了一个叶子节点，因此需要对后继删除的节点按照 “删除叶子节点” 的方式进行类似的处理
  
  

  删除了叶子节点之后需要对节点进行重平衡，具体如下：

  • 如果当前叶子节点在删除元素之后，元素个数依旧 \(>= M / 2\)​，那么就不需要进行重平衡
  • 如果当前节点的右节点存在多余的元素，那么：
    1. 将父节点的分隔元素移动到当前节点
    2. 由于父节点的分隔元素被移动下来了，这个时候就会将右节点的最小节点移动到分隔元素的原来的位置，使得节点重新平衡
  • 如果当前节点的左节点存在多余的元素，那么：
    1. 将父节点的分隔元素移动到当前节点
    2. 将左子节点的最右元素移动到原来父节点分隔元素所在的位置，使得节点重新平衡
  • 如果当前节点的左右节点都只有 \(M / 2\) 个元素，那么将选择一个节点和父节点中的分隔元素组合到一个节点中，具体地：
    1. 将分隔值添加到左节点
    2. 将右节点中的所有元素都移动到左节点
    3. 删除父节点中的分隔值，删除指向右节点的链接
    4. 由于父节点缺失了一个元素，因此父节点此时可能是不满足条件的，如果父节点是根节点并且此时没有元素了，那么将合并后的节点成为新的根节点（树的高度 -1）；如果父节点的元素数量 \(< m / 2\)​，那么需要重新平衡父节点

  如下示例所示：

  假设现在有一棵阶数 \(M = 5\) 的 B 树，初始状态如下所示：

  

  现在，将 \(3\)​ 所在的键值对进行删除，由于删除之后不会影响节点的平衡性，因此删除 \(3\) 之后的 B 树状态如下图所示：

  

  接着，再删除 \(10\) 所在的键值对，由于此时 \(10\) 所在的节点是一个叶子节点，删除 \(10\) 之后节点不再满足 “节点数 \(\geqslant M /2\)​ ” 这一条件，因此会检查左右兄弟节点是否存在多余的元素，左兄弟节点是存在多余的元素的，因此应用上文提到的策略，将父节点移动到当前节点的最左边，然后将左兄弟节点的最右元素放到父节点的分隔位置上，使得当前节点依旧满足条件，此时 B 树的状态如下图所示：

  

  接着再删除 \(7\) 所在的键值对，由于 \(7\)​ 所在的节点不是叶子节点，因此需要将最小的后继节点或者最大的前驱节点替换到当前位置，再重新调节当前节点的平衡，应用上文提到的规则，删除之后的状态如下图所示：

  

  同样地，删除 \(20\)​ 所在的键值对，删除之后 B 树的状态如下所示：
  

  这是一个中间状态，因此此时 \(17\) 所在的节点不满足条件，需要继续合并，最终结果如下图所示：

  

  说明：'*' 在图中表示的是一个哨兵键，不具备任何实际含义，因此不算入节点的元素总个数

复杂度分析

含有 \(N\) 个元素的 \(M\) 阶 B 树中一次查找或者插入需要 \(log_MN \longrightarrow log_{M/2}N\) 次探查，在实际情况下这基本是一个常数^[1]

实现

由于篇幅原因，具体的实现代码：https://github.com/LiuXianghai-coder/Test-Repo/blob/master/DataStructure/BTree.java

B+ 树

B+ 树和 B 树十分类似，不同的地方在于：

• B+ 树只用叶子子节点来存储实际数据元素，而非叶子结点不存储任何实际数据；
• B+ 树允许树中存在冗余的节点，即内存节点中出现的 \(key\) 可以再次在后继的子树中出现；
• B+ 树中各个叶子节点之间会相互连接，尽管这可能不符合树的定义，但是这样可以减少在树中对内部节点的搜索次数，从而提升性能

一棵 B+ 树看起来像下面这样：

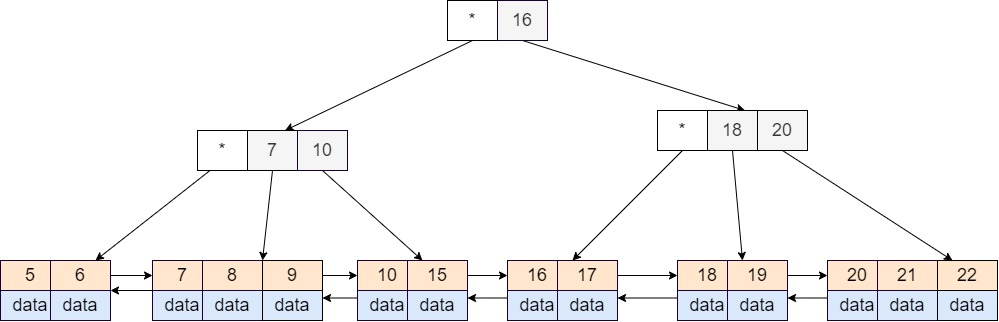
基本操作

• 查找

  查找和一般的二叉树的查找类似，不同的地方在于 B+ 树必须一直查找，直到到达叶子节点才能查找到对应的 \(key\) 的数据；其次，由于叶子节点之间的双端链接，在叶子节点之间也可以进行顺序查找

  有的关系型数据库会采用 B+ 树作为基本交互单元的存储结构（如 MySQL），由于叶子节点之间的双端链接，在执行如 BETWEEN 类型的语句时，能得到较大的性能提升

• 插入

  具体操作步骤如下：

  1. 如果此时根节点没有被填满，那么首先将键值对数据插入到根节点，此时根节点也是叶子节点
  2. 针对叶子节点：通过 \(key\)​ 找到叶子节点，向这个叶子节点插入对应键值对，如果此时该叶子节点依旧满足 B+树节点的限制（和 B 树一致），则完成；否则，需要将该节点进行分裂，从而使得该节点符合 B+ 树节点的限制
  3. 由于分裂时会将新的节点插入父节点，因此在递归回到父节点的时候，首先判断父节点是否需要分离，如果需要的话，则将节点继续向上递归处理

• 删除

  具体操作如下：

  1. 删除对应的叶子节点之后，如果此时叶子节点中的元素的个数依旧满足 B+ 树中节点的限制，则删除成功，否则，执行第二步
  2. 如果兄弟节点中存在多余的元素，首先将父节点移动到当前的叶子节点， 然后将兄弟节点中的最大（最小）元素替换掉父节点中的分隔节点
  3. 如果兄弟节点中也不存在多余的元素，那么将结合当前叶子节点中的左兄弟节点或者右兄弟节点，然后再删除父节点中二者的分隔节点；由于此时删除了父节点中的一个节点，因此可能会使得父节点中的节点个数不满足 B+ 树中对于节点数量的限制，此时需要递归地向上进行处理

实现

具体实现请参考：https://github.com/LiuXianghai-coder/Test-Repo/blob/master/DataStructure/BPlusTree.java

参考：

^[1] 《算法（第四版）》6.0.2.2 B- 树

^[2] https://www.cnblogs.com/nullzx/p/8729425.html