红黑平衡查找树
介绍
红黑平衡查找树是一种平衡的二叉树数据结构,最早由 鲁道夫·贝尔 在 1972 年提出,当时被称为 “对称二叉B树”。它的现代名字起源于 Leo J. Guibas 和 Robert Sedgewick 于 1978 年提出。相比较于 AVL 树,红黑树在调整时需要的操作更少,但是更加复杂,总体上性能要比 AVL 树更好。
感谢 Robert Sedgewick 对红黑树的讲解,尤其是在 《算法(第四版)》 中对于红黑树的全面介绍,使得我能够对于红黑树的学习能够如此简单。
起源
红黑树是基于 2-3 查找树演变过来的,通过为每个节点添加对应的红链接使得节点与 2-3 树中的节点对应起来,从而使得整个树是平衡的。因此,首先了解一下 2-3 树会使得学习红黑树变得简单。
2-3 查找树
一般情况下,对于一个二叉树的节点来讲,最多只有两个子节点,即左字节点和右子节点,这中节点我们称之为 2- 节点,如下图所示:
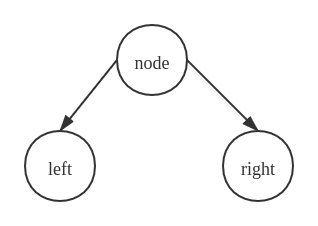
在不做任何处理的操作的前提下,使用这种节点构成的二叉树很难维持树的平衡性(可以试想一下插入一些有序的节点的情况)。为了维持树的平衡性,现在我们引入一个 3- 节点的概念,即允许两个节点组合成一个节点,使得这个节点可以有三个子节点。如下图所示:
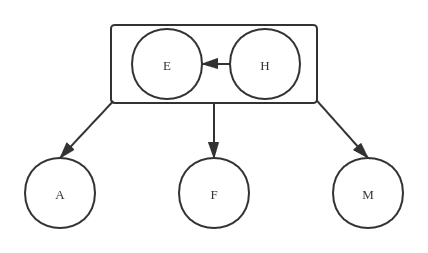
有了 3- 节点之后,当对一个 2- 节点新添加一个节点时,可以将它组合成为一个 3- 节点,情况要比只有 2- 节点 的二叉树要好一些了。但是光是这样是没有办法维持树的平衡的。现在,你可以尝试思考一下如何进行某些操作使得 2- 节点 和 3- 节点 在整个树中是平衡的。
给出的解决方案是再引入一个 4- 节点 的临时节点来处理 3- 节点 添加节点的情况,但是这种节点在我们的树中是不能够存在的(允许临时存在)。一旦出现了 4- 节点,就要立刻对它进行分解,将它拆分为三个 2- 节点。
4- 节点的示意图:
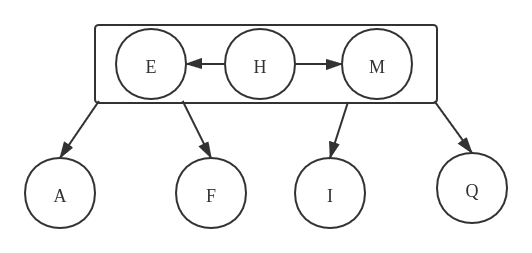
在当前的树中,不能存在 4- 节点,需要进行分解:
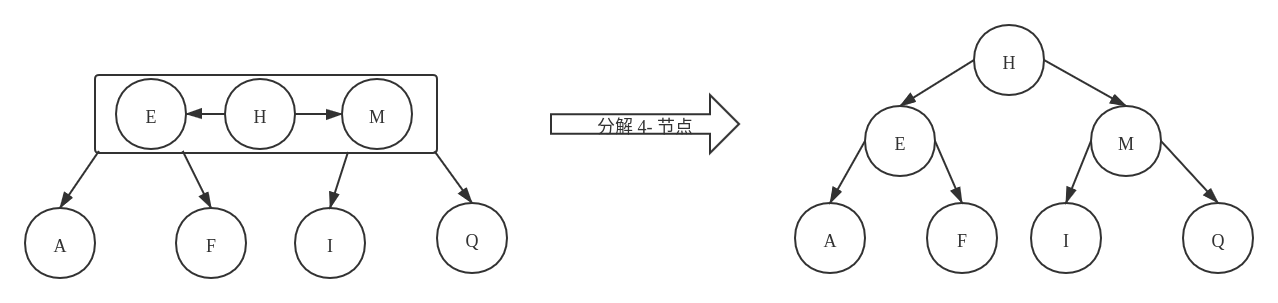
现在,让我们来看一下几种可能的插入情况:
-
插入的节点为空节点
- 这种情况只会对应根节点为空的情况,此时将根节点置为当前插入节点即可
-
插入的节点为2-节点
-
直接将当前的插入位置的 2- 节点 转换为一个 3- 节点
以下图插入
A为例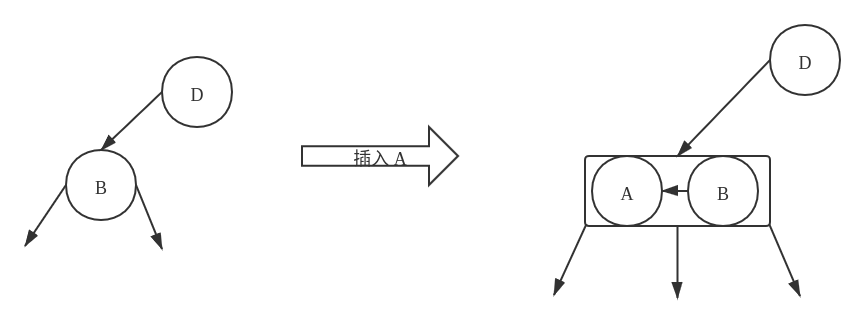
-
-
插入的节点为 3- 节点
-
插入的 3- 节点的父节点为 2- 节点
这种情况下首先将待插入的节点插入到 3- 节点 中,使得 3- 节点成为一个 4- 节点,再将这个 4- 节点进行分解,使得 父节点成为一个 3- 节点
依旧以上文的例子为例,现在我们在上面的树中插入节点
C: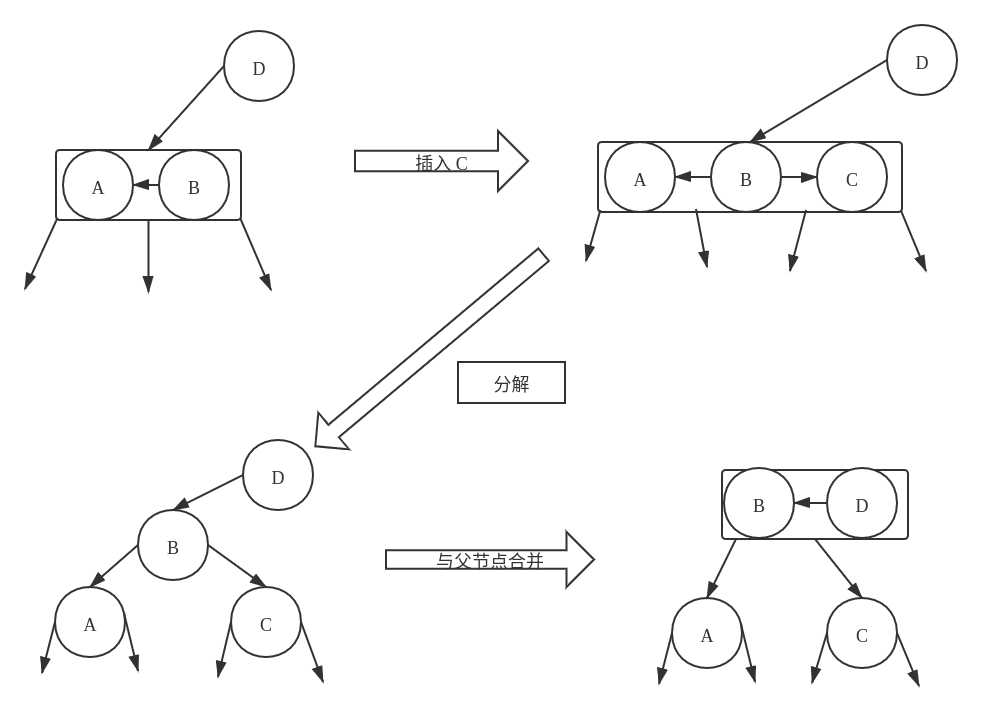
-
插入的 3- 节点的父节点为 3- 节点
在这种情况下,首先插入节点,使得当前的 3- 节点 转换为一个 4- 节点,然后将这个 4- 节点分解,使得父节点成为一个 4-节点。注意,这里的父节点的 4- 节点 只是临时存放的。
转换关系如下图所示:
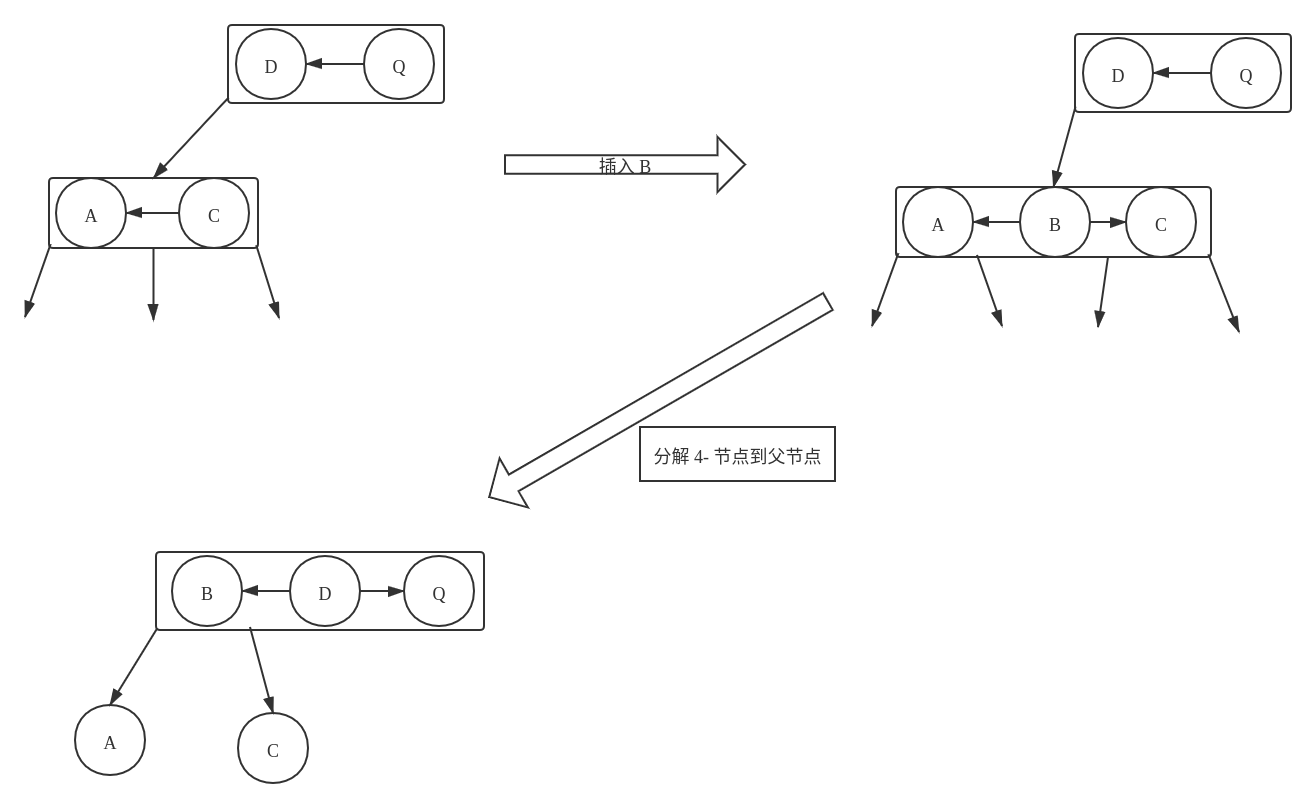
-
由于在插入时会调整节点在 3- 节点 和 4- 节点 中的位置,因此最终得到的树是一颗完美平衡的树。你可以尝试模拟一下插入节点的过程,这对于理解 2-3 查找树来讲非常关键。
红黑树
红黑树就是基于 2-3 查找树,通过一些特定的操作来模拟 2-3 树的操作。为了与上文的 2-3 查找树对应,现在对节点引入红链接和黑黑链接两个概念。
-
红链接
表示当前的节点与父节点组合成了一个 3- 节点
将红链接节点与父节点之间的链接画平,可能会容易理解一些:
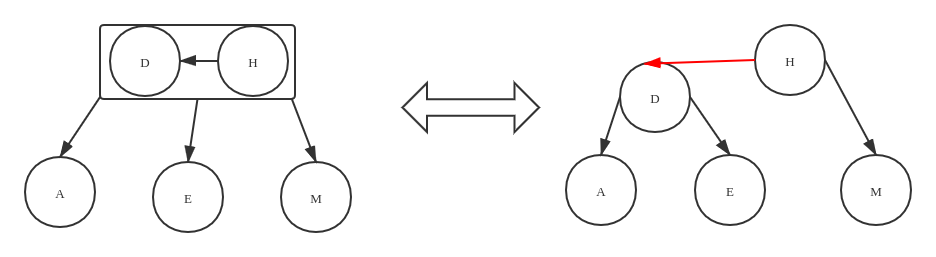
-
黑链接
表示当前的节点就是一个普通的 2- 节点
定义
一颗树是否为红黑树,它要同时满足以下三个条件
- 红链接均为左链接
- 没有任何一个节点同时和两条红链接相连
- 该树是完美黑色平衡的(即任意叶子节点到根节点的黑色链接的数量是相等的)
旋转操作
在插入节点时,会自动将当前的节点置为红链接节点,为了能够将插入的节点调整到正确的位置,我们需要引入旋转的操作来完成。
-
左旋转
示意图如下:
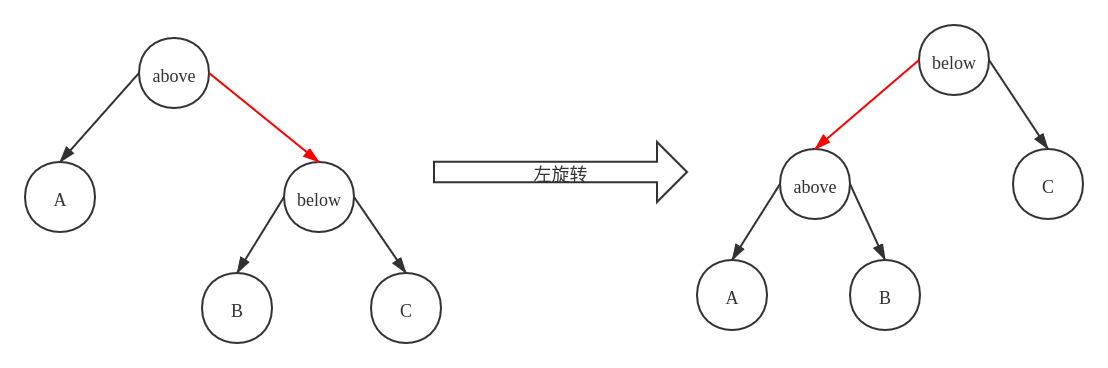
-
右旋转
示意图如下:

颜色转换
当一个父节点的两个子节点都是红链接节点时,此时父节点对应 2-3 节点的 4- 节点,需要进行分解。巧妙的是,只需要将每个节点的颜色转换为原来相反的颜色即可
转换关系如下图所示:
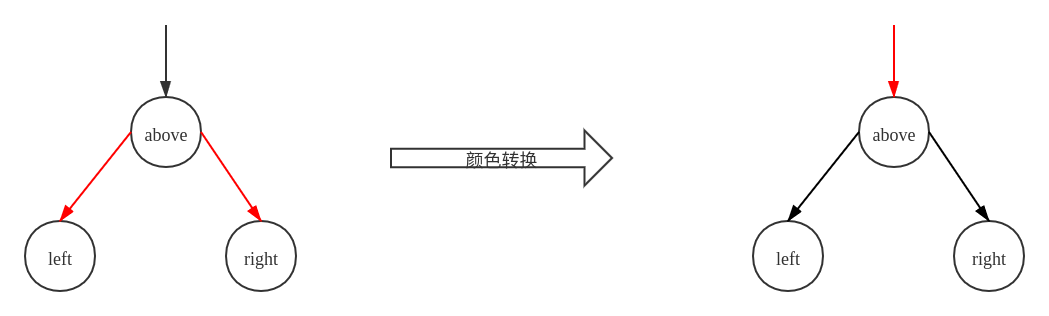
转换规则
对于插入的节点,会默认它是一个红链接节点。因此,当插入一个节点时,可能会出现以下几种情况:
- 父节点是一个黑链接节点
- 如果当前的插入位置是左节点,那么无需进一步的操作
- 如果当前插入的位置是右节点,那么需要将这个父节点进行一次左旋转
- 父节点是一个红链接节点
- 如果当前插入的位置是左节点,那么此时父节点同时具有两个红链接。这种情况下需要把父节点的父节点首先进行一次右旋转,使得父节点成为一个 4- 节点,然后再进行颜色转换进行分解。
- 如果当前插入位置是右节点。这中情况下要首先对父节点进行一次左旋转,转变父节点同时持有两个红链接的情况,再按照对应的方式进行处理。
具体的转换规则如下图所示(取自《算法(第四版)》):
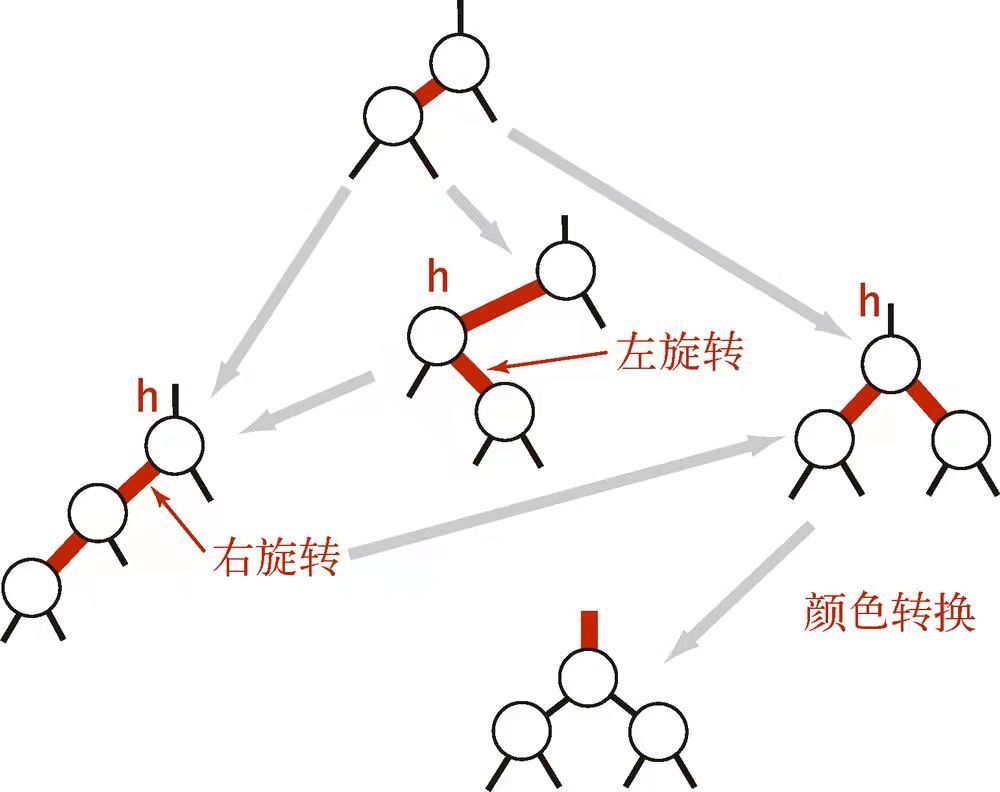
你可以尝试插入一些元素,以增强对于它的理解。转换时记得与 2-3 查找树进行对应,这是理解红黑树的关键。
插入操作
有了上文的转换规则,插入一个元素就变得简单多了,只需要在插入一个元素之后进行上文提到的转换规则进行适当的变换就可以了。
// 定义节点类
private static class Node<T extends Comparable<T>>
implements Comparable<T> {
private T val;
private Node<T> left, right;
private boolean color;
private int size;
public Node(T val) {
this.val = val;
}
public T getVal() {return this.val;}
public void setLeft(Node<T> left) {this.left = left;}
public Node<T> getLeft() {return this.left;}
public Node<T> getRight() {return right;}
public void setRight(Node<T> right) {this.right = right;}
public void setSize(final int size) {this.size = size;}
public int getSize() {return this.size;}
@Override
public int compareTo(T o) {
return this.getVal().compareTo(o);
}
public boolean isColor() {
return color;
}
public void setColor(boolean color) {
this.color = color;
}
}
插入操作:
public void add(Node<T> node) {
root = add(root, node);
root.color = BLACK;
}
/*
添加一个节点,添加时将这个节点的颜色置为红色,对于一个添加的节点,可能有以下几种情况
1. 添加的位置为左子节点
1> 对于父节点为黑链接的情况,直接插入即可
2> 对于父节点为红链接的情况,首先需要对父节点进行一次右旋转,再进行一次颜色转换
parent left left
// \ // \\ / \
left right ======> node parent ====> node parent
// \ \
node right right
2. 添加的位置为右子节点
1> 如果父节点的左子节点为黑链接,只需对父节点进行一次左旋转即可
parent parent
\\ //
node =====> node
2> 如果父节点的左子节点为红链接,那么需要进行一次颜色转换
parent parent
// \\ / \
left node =====> left node
3> 如果父节点为红链接,那么需要首先对父节点进行一次左旋转,
再对父节点的父节点进行一次右旋转,再进行一次颜色转换
// //
parent parent parent parent
\\ // // \\ / \
node ======> node ====> node =====> node
*/
private Node<T> add(Node<T> parent, Node<T> node) {
if (parent == null) {
Node<T> node1 = new Node<>(node.val);
node1.size = 1;
node1.color = RED;
return node1;
}
int compare = parent.compareTo(node.val);
if (compare > 0)
parent.left = add(parent.left, node);
else if (compare < 0)
parent.right = add(parent.right, node);
else
parent.val = node.val;
if (isRed(parent.left) && isRed(parent.right))
flipColor(parent); // 允许临时存在 4- 节点
if (isRed(parent.right) && !isRed(parent.left))
parent = rotateLeft(parent, parent.right);
if (isRed(parent.left) && isRed(parent.left.left))
parent = rotateRight(parent, parent.left);
parent.size = getSize(parent.left) + getSize(parent.right) + 1;
return parent;
}
以插入 {13, 4, 9, 7, 5, 34, 8, 6} 节点为例,大致的插入流程如下图所示:
-
插入13
此时 2-3 树和红黑树都只有一个节点,即根节点

-
插入 4
在 2-3 树中将原来的 2- 节点转换为 3- 节点;在红黑树中就是插入一个左红链接节点,无需进一步的操作

-
插入 9
在 2-3 树中,此时的根节点为一个 4- 节点,需要对它进行分解操作
2-3 树:
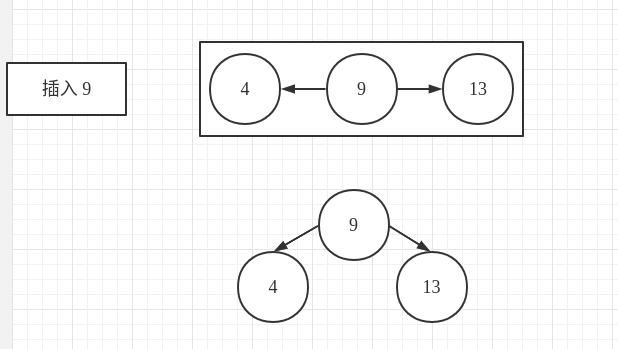
在红黑树中,由于此时插入的位置是 4 节点的右红节点,因此首先需要对 4 节点进行一次左旋转,然后再对根节点进行一次右旋转,最后进行一次颜色转换即可。
红黑树:
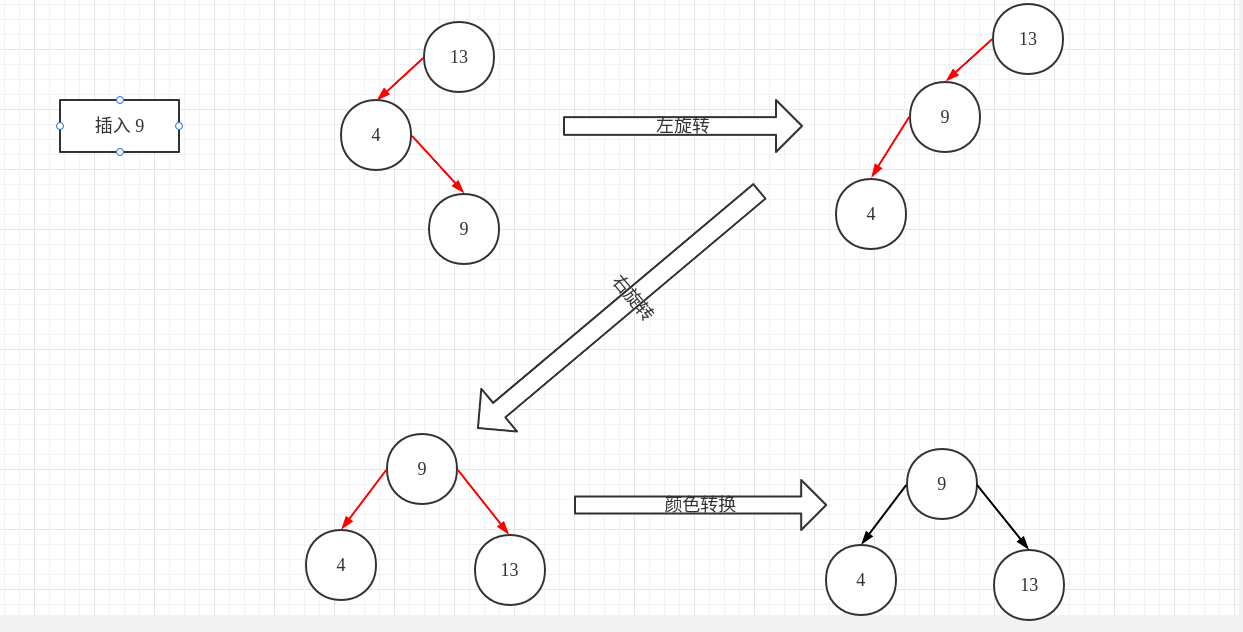
注意观察旋转操作是如何将 9 放到根节点的。
-
插入7
2-3 查找树:找到插入位置,当前的插入位置为 4节点,因此将 4节点转换为一个 3- 节点即可
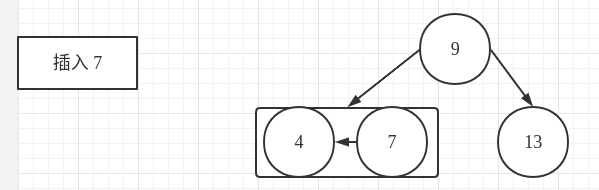
红黑树:
找到插入位置,同样的也是 4节点,但是插入的位置是 4节点的右子节点,因此需要对 4节点进行一次左旋转
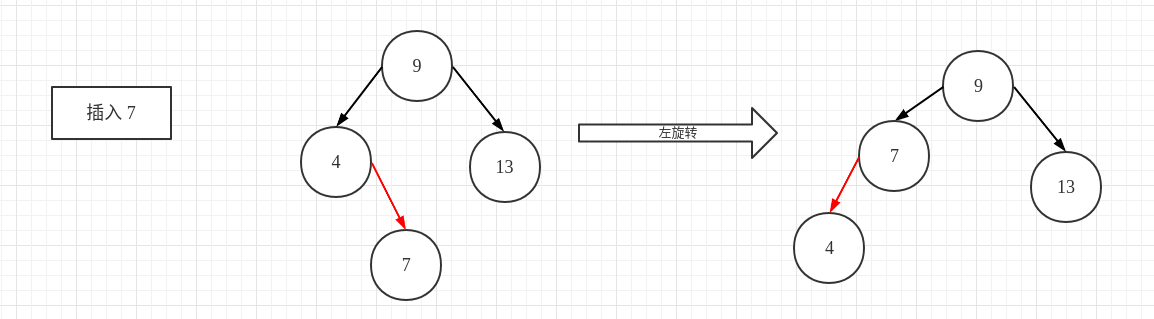
-
插入 5
2-3 树:插入 5 到 4、7 节点组成的 3- 节点 中,使得这个 3- 节点成为一个4-节点,然后进行分解,分解后的父节点将会与根节点组合成为一个新的 3- 节点
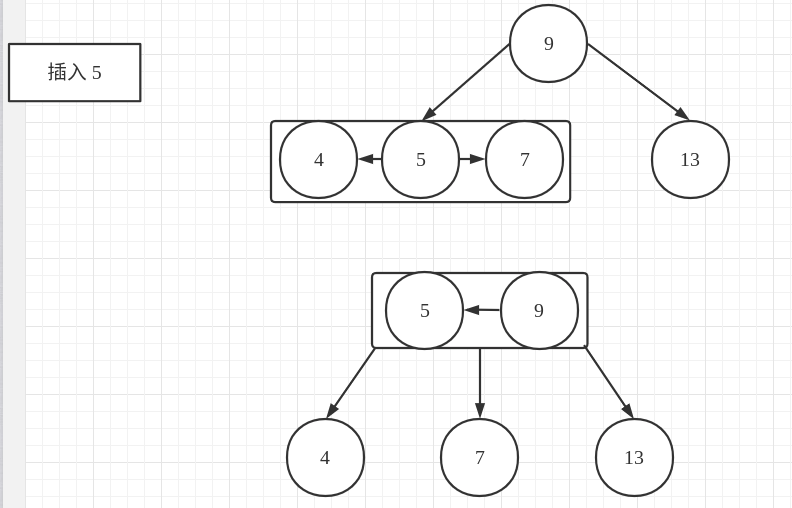
红黑树:找到待插入的节点,这里的节点依旧是 4节点,由于插入的位置是右子节点,因此首先需要对 4节点进行一次左旋转,左旋转之后 5节点存在两条红链接,按照上文提到的转换规则,需要对 5节点的父节点进行一次右旋转,此时 5结点将会成为新的父节点。然而,此时的 5节点两个子节点都是红链接,这就相当于 2-3 树中的 4- 节点,需要对它进行分解。分解操作就对应着上文提到的颜色转换。
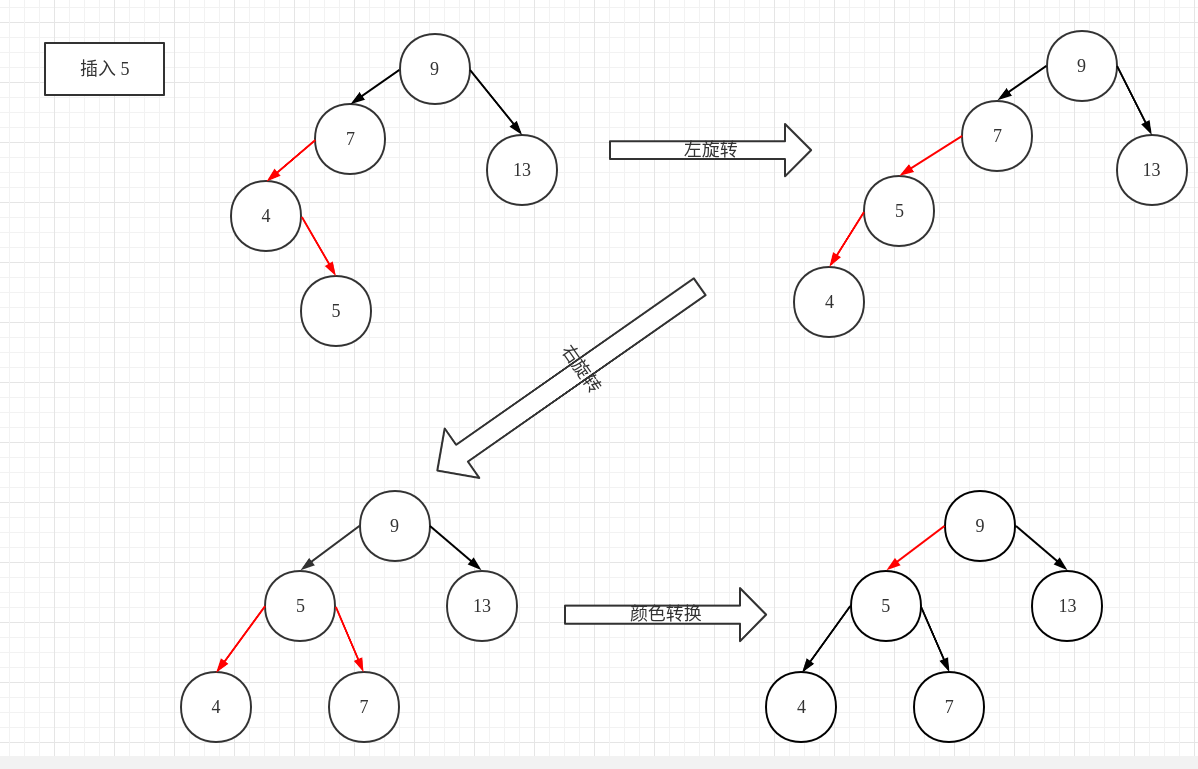
请再次观察一下红黑树是如何与 2-3 树对应起来的。
-
插入 34
2-3 树:同样的,找到插入的节点,这里的待插入节点时 13节点,由于它是一个 2- 节点,因此只需要将 13节点转换为一个 3- 节点即可。
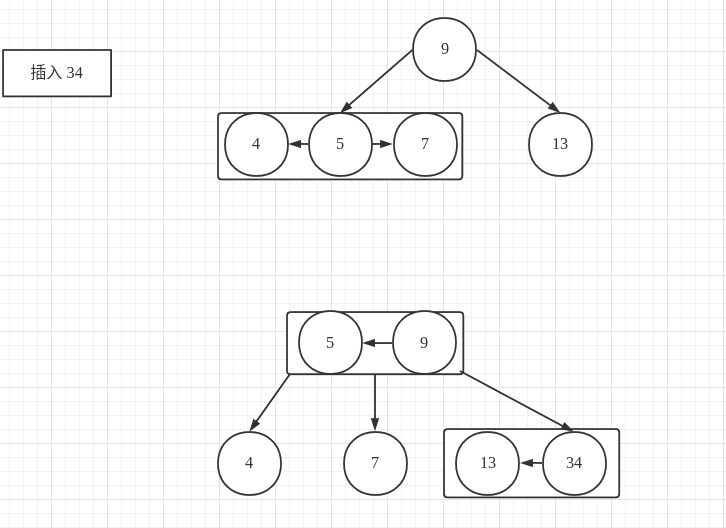
红黑树:同上文一致,找到要插入的元素的位置,这里是 13节点,由于插入的位置是右子节点,因此需要对 13节点进行一次左旋转,从而达到与 2-3 树相似的效果。
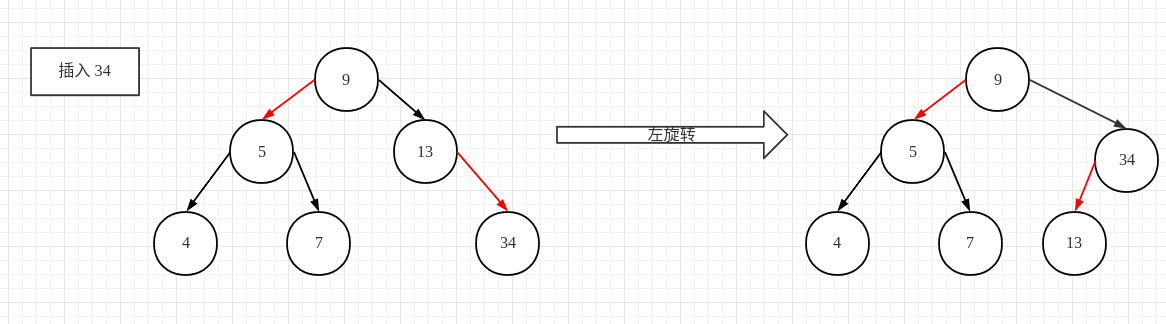
-
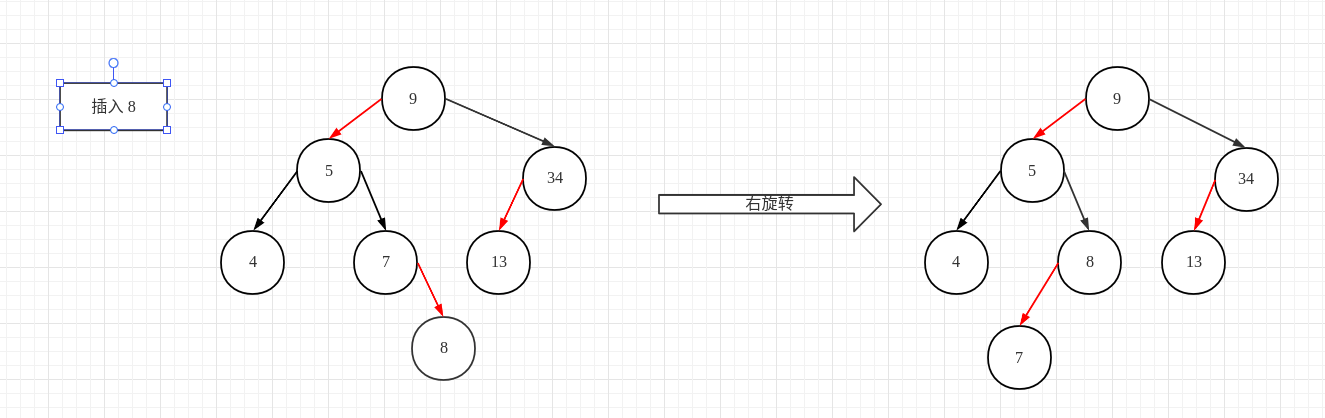
插入 8
2-3 树:
当前的插入位置在 7节点,由于 7节点依旧是一个 2- 节点,因此只需将 7节点转换为一个 3- 节点即可。
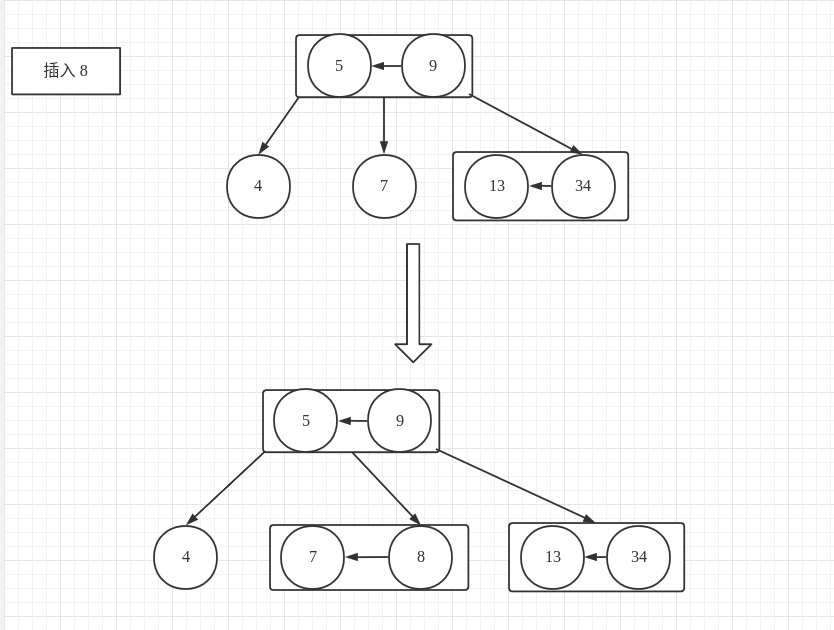
红黑树:同样的,插入的目标节点在 7节点,由于插入的位置在右子节点,因此需要对 7节点进行一次左旋转
-
插入 6
2-3 树:插入的节点位置在由 7、8 节点组成的 3-节点,当插入 6时,使得这个 3- 节点成为一个4-节点,由于 4- 节点不能稳定地存在,因此需要对它进行分解,分解之后的两个 2- 节点 的父节点又与父节点的 3- 节点 组成了一个 4- 节点,同样需要进行分解。
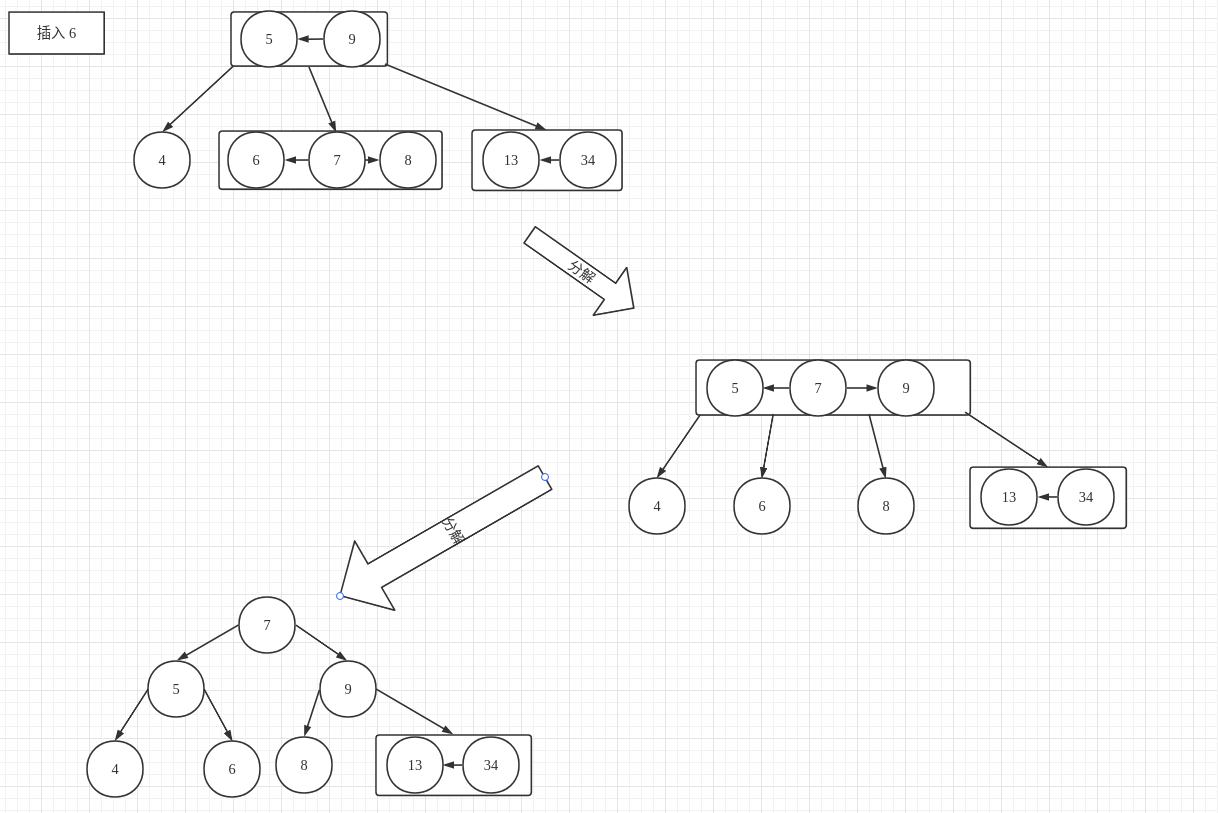
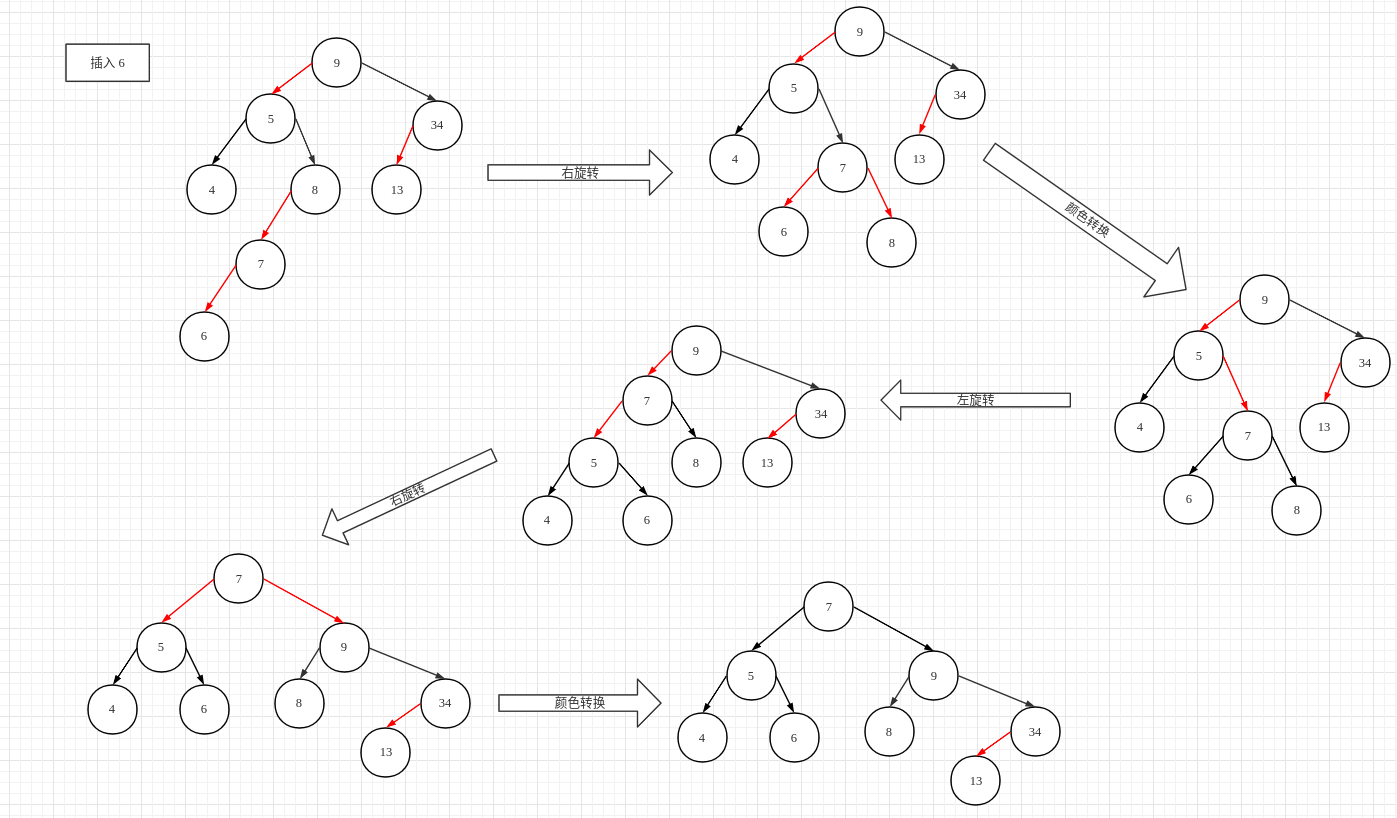
红黑树:具体过程如下图所示(注意与 2-3 树进行对照):
删除操作
删除操作是红黑树中实现较为困难的部分。具体的实现思路:在 3- 节点 中删除元素不会影响到树的平衡性,因此要尽量使得待删除的节点处于一个 3- 节点 中。
为了能够将一个 2- 节点放入一个 3- 节点,在树的构建过程中允许 4- 节点临时出现
对于一个要删除的节点来讲,存在以下几种情况:
-
待删除的节点在一个 3- 节点 或者 4- 节点中
在这种情况下不需要做额外的处理,只需要正常地删除这个节点,然后小心地旋转父节点配平就可以完成删除的任务,而且不会影响到树的平衡性。
-
待删除的节点是一个 2- 节点
这种情况下,又分为以下几种情况
-
父节点是一个 2-节点
-
兄弟节点是一个 2- 节点
这种情况下,可以和父节点、兄弟节点组合成为一个 4- 节点。
-
兄弟节点是一个非 2- 节点 (3- 节点或者 4- 节点)
这种情况下一般的做法是从兄弟节点借一个节点放到父节点的位置,使得当前节点和父节点构成一个新的 3- 子节点
-
-
父节点是一个非 2- 节点
-
兄弟节点是一个 2- 节点
这种情况下可以将父节点从原来的节点中剥离出来,使得父节点、当前节点、兄弟节点重新构成一个新的 4- 节点
-
兄弟节点是一个非 2- 节点
这种情况下同样需要把父节点从原来的节点中剥离出来,不同的地方在于,这这种情况下会将兄弟节点中的一个节点放到当前父节点的位置,同时将父节点与当前的处理节点组合成为一个新的 3- 节点
-
-
具体的规则如下图所示(取自《算法(第四版)》):
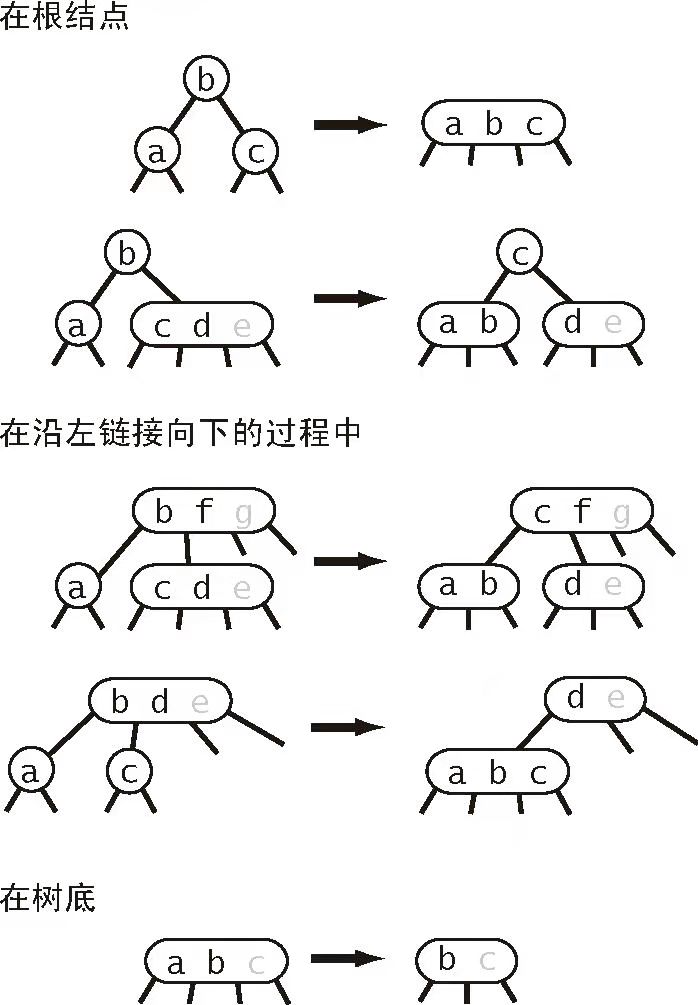
实现:
public void delete(Node<T> node) {
if (root == null) {
throw new RuntimeException("当前根节点为空");
}
if (!isRed(root.left) && !isRed(root.right))
root.color = RED;
root = delete(root, node);
if (!isEmpty()) root.color = BLACK;
}
private Node<T> delete(Node<T> parent, Node<T> node) {
if (node.compareTo(parent.val) < 0) {
if (!isRed(parent.left) && !isRed(parent.left.left))
parent = moveRedLeft(parent);
parent.left = delete(parent.left, node);
} else {
if (isRed(parent.left))
parent = rotateRight(parent, parent.left);
if (node.compareTo(parent.val) == 0 && parent.right == null)
return null;
if (!isRed(parent.right) && !isRed(parent.right.left))
parent = moveRedRight(parent);
if (node.compareTo(parent.val) == 0) {
Node<T> x = min(parent.right);
parent.val = x.val;
parent.right = delMin(parent.right);
} else {
parent.right = delete(parent.right, node);
}
}
return balance(parent);
}
以上代码参考了一部分 《算法(第四版)》 中的实现,按照它的实现最后删除节点得到的树不是一棵严格意义上的红黑树,但是它依旧是满足 “完美黑色平衡” 这一条件的,在实际应用这并不会有太大的影响
具体的实现:https://github.com/LiuXianghai-coder/Test-Repo/blob/master/DataStructure/RedBlackBST.java
如果觉得觉得我讲的不是很清晰,那么我建议可以去阅读一下 《算法(第四版)》中关于红黑树的这一部分。这个作者讲述的会比我的更加清晰、更加易懂。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号