动态规划问题(六)最长公共子序列(LCS)
问题描述
给你两个字符串,要求得到这两个字符串的最长公共子序列长度。
比如:对于输入的字符串 S1 "AGGTAB" 和 S2 "GXTXAYB",它们的最长公共子序列长度为 4,为 {'G', 'T', 'A', 'B'}
解决思路
该问题刚开始见到时没有思路,但是把问题细分一下找到规律即可解决。
-
递归
-
对于当前输入的两个字符串,可以通过不断将两个字符串的分别移除来减小问题的规模,最终收敛
-
以上文的输入为例,对于输入的 S1 “AGGTAB” 和 S2 “GXTXAYB”,首先将 S1 的第一个字符与 S2 的第一个字符比较,然后移除 S1 的第一个字符再与 S2进行比较…… 对 S2 做同样的操作。此时的情况如下图所示:
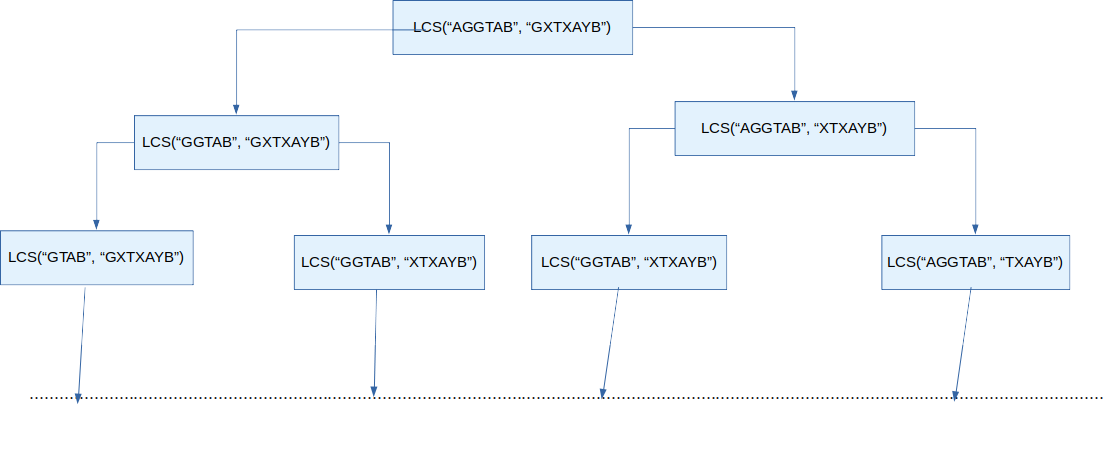
-
-
动态规划
- 动态规划在这里的解决的是重复子问题的类型,由于上文的递归方案,在这个解决过冲中存在大量的重复计算,因此可以使用动态规划存储中间计算结果,从而提高运行效率。
实现
-
递归
public class Solution { public static int lcs(String s1, String s2) { int len1 = s1.length(), len2 = s2.length(); // 递归终止条件 if (len1 == 1 || len2 == 1) return s1.charAt(0) == s2.charAt(0) ? 1 : 0; // 递归剩下的结果得到该问题的解 if (s1.charAt(0) == s2.charAt(0)) return Math.max( lcsRecur(s1.substring(1), s2), lcsRecur(s1, s2.substring(1)) ) + 1; return Math.max( lcsRecur(s1.substring(1), s2), lcsRecur(s1, s2.substring(1)) ); } } -
动态规划
public class Solution { public static int lcs(String s1, String s2) { // 将字符串转变为对应的字符数组,提高查找的速度 char[] s1Arr = s1.toCharArray(); char[] s2Arr = s2.toCharArray(); int row = s1Arr.length, col = s2Arr.length; // 存储中间计算结果的二维数组 int[][] dp = new int[row + 1][col + 1]; for (int i = 1; i <= row; ++i) { for (int j = 1; j <= col; ++j) { if (s1Arr[i - 1] == s2Arr[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1; // 由于要保证当前的字符是在之前比较的字符之后的,因此需要得到的是左上角的元素中间值 else dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]); } } return dp[row][col]; } }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号