数据结构(二):括号匹配(C++,栈)

好家伙,写题,题目代码在最后

 

来吧,

 

 

1.栈 

栈（stack）又名堆栈，它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。

这一端被称为栈顶，相对地，把另一端称为栈底。

向一个栈插入新元素又称作进栈、入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；

从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。 　　　　　　　　                                                                                                                                                                                                                                                        　　　　　　　　　　　　　　　　——百度百科　　

上图

 

 

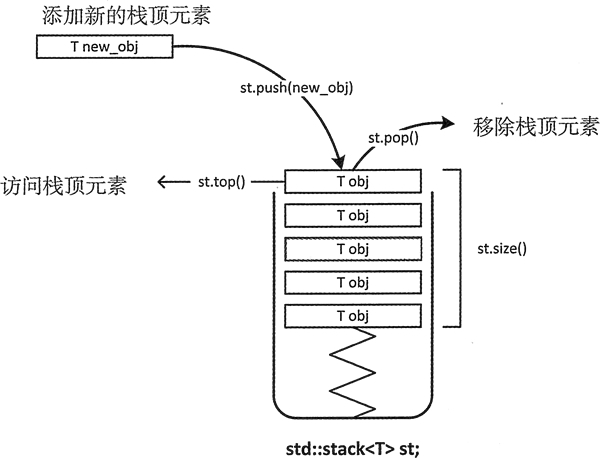
 总之,我们记住这玩意"先进后出"就行了

举个栗子,(假设水倒入杯子后不会流动)

就像你烧了一壶水,拿个杯子倒水,然后喝了一口

你喝的第一口水是你最后倒进去的

而你最先倒进去的水在最下面

 

最后倒进去的水最先喝到

最先倒进去的最后喝到

这就是先进后出了

(是不是拿固体举例子会比较好...)

 

 

方法以及标识:

//头文件
#include <stack>

//实例化字符类型的栈
stack <char> sta;

常用方法:

1.1.sta.top()方法

函数用于访问栈顶元素

 

1.2.sta.pop()

函数用于移除栈顶元素

 

1.3.sta.size()

函数返回堆栈元素的数量。堆栈元素的数量是指堆栈的大小。

堆栈元素的大小是非常重要的信息，因为基于它我们可以推断出许多其他内容，例如所需的空间等。

 

1.4.sta.push(new_obj)

函数用于在栈顶添加新元素

 

1.5.sta.empty()

函数用于测试容器是否为空

 

 

 

 

2.题目如下:

输入一串字符串，该字符串只能由各种不同的括号组成，设计算法，测试该字符串中的括号是否匹配。

如：“({[]})”该字符串中括号是匹配的，字符串“[{{}(”是不匹配的，要求采用栈的思想来完成该题目

 

 

 

2.1.分析一波题目:

我们用栈去解决这个题目(不然为什么会有上面的内容)

这种对称的题目用栈来做就是很舒服

利用栈的先进后出的特点，我们可以进行左右括号的匹配，“（）{}”,在右括号“）}”左边最近的左括号必须是相对应的“（{”，否则就不合法
先把左半边的括号全部入栈,然后按入栈的反顺序依次去查对应右括号,(如先入"{("那么就先查")}")

若果出现不匹配,则返回false,

每次匹配一对正确的括号，就要将其出栈，为后面的括号腾出空间。

 

上代码:

#include <iostream>
#include <stack>

using namespace std;

    bool isValid(string s) {
        stack <char> sta;
        char c,b;
        int l=s.length();
       for(int i=0;i<l;i++)
              {
                //将所有的左半边括号入栈 
                  if(s[i]=='(' || s[i]=='[' || s[i]=='{')
                        {
                            sta.push(s[i]);
                        }
                        //对后面的元素逐一检查
                        //三种情况
                        //1.栈空了,返回false 
                        //2.成功匹配,将成功匹配的字符出栈 
                        //3.其他情况,返回false 
                        else if(s[i]==')')
                        {
                            if(sta.empty())
                                return false;
                            else if(c=sta.top(),c=='(')
                                    sta.pop();
                            else
                                return false;
                        }
                        else if(s[i]==']')
                        {
                              if(sta.empty())
                                return false;
                            else if(c=sta.top(),c=='[')
                                    sta.pop();
                            else
                                return false;
                        }
                        else if(s[i]=='}')
                        {
                              if(sta.empty())
                                return false;
                            else if(c=sta.top(),c=='{')
                                    sta.pop();
                            else
                                return false;
                        }
              }
              if(sta.empty())
                return true;
              else
                return false;
    }
    
int main()
{
   string s;
   cin>>s; 
   //输入字符 
   bool b=true;

   b=isValid(s);
   if(b==true)
   cout << "true";
   else cout << "false";
    return 0;
}

 

 

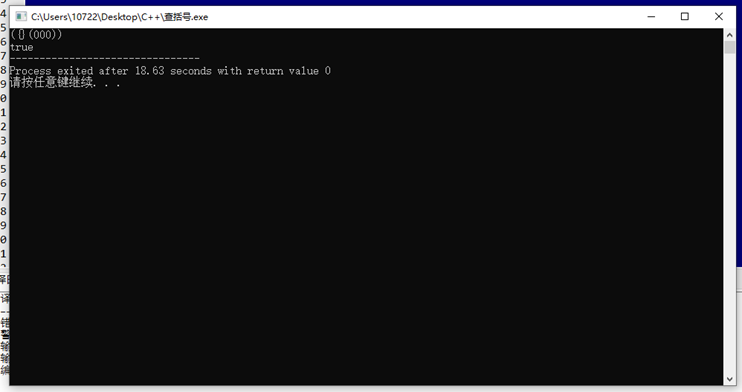
输入样例:

输入: ({}(000))

输出: true