C语言：多功能计算器 (矩阵相乘)
好家伙，实现矩阵相乘功能
代码如下：
void fifth()//矩阵的相乘//
{
int a[100][100],b[100][100];
int d,e,f,h,j,k,t;
double sum;
double c[100][100];
printf("请输入第一个矩阵行数和列数；\n");
scanf("%d%d",&d,&e);
printf("请输入矩阵中的数字：\n");
for(f=0;f<d;f++)
{
for(h=0;h<e;h++)
{
printf("请输入第%d行第%d列的数字",f,h);
scanf("%d",&a[f][h]);
}
}
printf("请输入第二个矩阵行数和列数.\n");
scanf("%d%d",&j,&k);
printf("请输入矩阵中的数字：\n");
for(f=0;f<j;f++)
{
for(h=0;h<k;h++)
{
printf("请输入第%d行第%d列的数字",f,h);
scanf("%d",&b[f][h]);
}
}
if(e==j)//矩阵相乘只有在左边矩阵的列数等于右边矩阵的行数时才能相乘
{
for(f=0;f<d;f++)
{
for(h=0;h<k;h++)
{
sum=0;
for(t=0;t<e;t++)
{
sum+=a[f][t]*b[t][h];
}
c[f][h]=sum;
}
printf("\n");
}
for(f=0;f<d;f++)
{
for(h=0;h<k;h++)
{
printf("%6.2f",c[f][h]);
}
printf("\n");
}
}
else
{
printf("该输入的矩阵无法相乘，因为输入左边的矩阵的列数不等于右边矩阵的行数。\n");
}
}
2. (fifth)函数 矩阵的相乘
核心算法部分:
(按照公式计算出最终矩阵的值,其中d,e是第一个矩阵的行数和列数,j,k是第二个矩阵的行数和列数)
for(f=0;f<d;f++)
{
for(h=0;h<k;h++)
{
sum=0;
for(t=0;t<e;t++)
{
sum+=a[f][t]*b[t][h];
}
c[f][h]=sum;
}
算法分析:
此处使用三个for循环,
第一层for循环控制第一个矩阵的行数(f),
第二层for循环控制控制第一个矩阵的列数和第二个矩阵的行数,(t)
第三个for循环控制第二个矩阵的列数,(h)
以（t++）为点
测试样例:
输入:2 3\n 1\n 2\n 3\n 4\n 5\n 6\n
2 3\n 1\n 2\n 3\n 4\n 5\n 6\n
输出:7.00 10.00
19.00 28.00
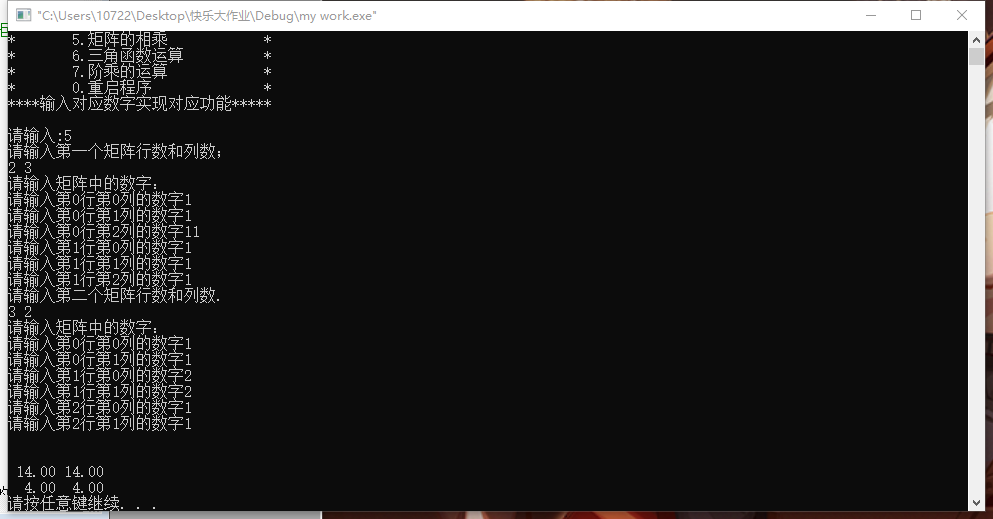
测试图片：
