题解 CF573B 【Bear and Blocks】

\[\text{拆方块} \]

\(\quad\)表示完全看不懂其他 \(dalao\) 的线段树， \(st\) 表和曼哈顿最小生成树做法，于是自己写一发题解帮助其他像我一样的蒟蒻。

\(\quad\)首先我们不应该把方块看做一个一个的，而是一列一列的，\(l\) , \(r\) 分别来表示这列方块因左边，右边无方块而消失的时间，设这列方块的编号为 \(i\) ，消失时间为 \(f_i\) ，高度为 \(h_i\) ，设左边那列的方块消失时间为 \(f_{i-1}\)，设右边那列的方块消失时间为 \(f_{i+1}\) ，显然可以得到

\[f_i=\min(f_{i-1}+1,f_{i+1}+1,h_i) \]

\(\quad\)因为当左边的方块全部消失时，这列方块显然会在下一个时间消失(若这列方块之前没有消失)，当右边的方块全部消失时，这列方块显然会在下一个时间消失(若这列方块之前没有消失)，又因为每个时间每一列方块的高度会减 \(1\) ，显然一列方块 \(i\) 最多在 \(h_i\) 时消失，所以可以得到

\[l_i=\min(l_{i-1}+1,h_i \]

\[r_i=\min(r_{i+1}+1,h_i) \]

\(\quad\)这需要两遍循环处理，从小到大循环处理 \(l_i\) ，从大到小处理 \(r_i\) ，最后第 \(i\) 列方块消失的时间就是 \(\min(l_i,r_i)\) 。

\(\quad\)如果还不理解就看看样例理解一下。

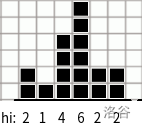
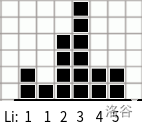
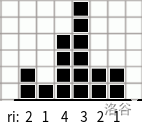
\(\quad\)注意一定要先更新高度，将 \(l_i\) 和 \(r_i\) 初始化为 \(h_i\) 即可，如上面第二列，后面 \(l_i\) 和 \(r_i\) 都会受到高度的影响。

\(\quad\)极简代码，关键只有三行！！

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
#define re register int
#define int long long
#define il inline
il int read()
{
  int x=0,f=1;char ch=getchar();
  while(!isdigit(ch)&&ch!='-')ch=getchar();
  if(ch=='-')f=-1,ch=getchar();
  while(isdigit(ch))x=(x<<1)+(x<<3)+ch-'0',ch=getchar();
  return x*f;
}
il void print(int x)
{
  if(x<0)putchar('-'),x=-x;
  if(x/10)print(x/10);
  putchar(x%10+'0');
}
const int N=1e5+5;
int n,ans,l[N],r[N];
signed main()
{
  n=read();
  for(re i=1;i<=n;i++)l[i]=r[i]=read();//初始化大小为高度
  for(re i=1;i<=n;i++)l[i]=min(l[i],l[i-1]+1);//处理l数组
  for(re i=n;i>=1;i--)r[i]=min(r[i],r[i+1]+1);//处理r数组
  for(re i=1;i<=n;i++){ans=max(ans,min(r[i],l[i]));}//取最大的较小值
  print(ans);
  return 0;
}