题解 P1505 【[国家集训队]旅游】
\(\quad\)一道很简单毒瘤的树链剖分练习题,只有五种操作,除了码量较大,就没有什么其他特点了,是一道很好的练习题。可以锻炼\(OIer\)找错能力,我调了一个小时, \(WA\)了一次
\(\quad\)有几道题也是树链剖分边权转点权,可以先去做一下:P4114 Qtree1,P3950 部落冲突(我的题解),CF165D Beard Graph(我的题解)。
\(\quad\)考虑到树上有 \(n\) 个点,有 \(n-1\) 条边,并且每个点有且只有一个父亲节点(除了根节点),但是每个点可能有多个儿子(也可能没有),所以我们可以将边权转化为儿子节点的点权(深度更大的点),这样除了根节点,\(n-1\) 条边就合理的分配到 \(n-1\) 个点上。(如果还不能就看看图吧)
原图
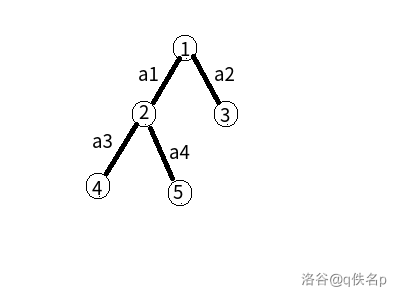
经过转化后的图(将边权转化为点权)

\(\quad\)注意:对于路径\(4-2-5\),只需访问点 \(4\) 和点 \(5\),对于 \(4\) 和 \(5\) 的 \(LCA\) (最近公共祖先)不可取,因为 \(2\) 在原图中对应的是边 \(1-2\),并不在路径\(4-2-5\)上,所以在树链剖分中当 \(x\) 和 \(y\) 在同一条链上时(\(dep[x]<dep[y]\)),只需询问 \(x+1\) 到 \(y\) 的路径。
il void dfs1(int x,int fa,int ss) //ss表示x与fa(x的父亲)的连边的权值
{
father[x]=fa;dep[x]=dep[fa]+1;size[x]=1;a[x]=ss;
for(re i=head[x],y;i,y=go[i];i=next[i])
{
if(y==fa)continue;
dfs1(y,x,s[i]);
size[x]+=size[y];
if(size[y]>size[son[x]])son[x]=y;
}
}
il int query1(int x,int y,int z)
{
int fx=top[x],fy=top[y],res;
if(z==1)res=0;
else if(z==2)res=-10000;
else if(z==3)res=10000;
while(fx!=fy)
{
if(dep[fx]<dep[fy])swap(x,y),swap(fx,fy);
if(z==1)res+=query(1,1,n,seg[fx],seg[x],z);
else if(z==2)res=max(res,query(1,1,n,seg[fx],seg[x],z));
else if(z==3)res=min(res,query(1,1,n,seg[fx],seg[x],z));
x=father[fx];fx=top[x];
}
if(dep[x]>dep[y])swap(x,y);
if(seg[x]==seg[y])return res;
if(z==1)res+=query(1,1,n,seg[x]+1,seg[y],z);//最后一次询问是seg[x]+1到seg[y]
if(z==2)res=max(res,query(1,1,n,seg[x]+1,seg[y],z));//最后一次询问是seg[x]+1到seg[y]
if(z==3)res=min(res,query(1,1,n,seg[x]+1,seg[y],z));//最后一次询问是seg[x]+1到seg[y]
return res;
}
- 操作1:单点修改,输入 \(C\) \(i\) \(w\) 将输入的第 \(i\) 条边权值改为 \(w\) ,找出第 \(i\) 条边的两个端点,修改儿子节点
il void change3(int x,int y)
{
int xx=go[x<<1],yy=go[(x<<1)-1];
if(xx==father[yy])change1(1,1,n,seg[yy],y);
else change1(1,1,n,seg[xx],y);
}
-
操作2:区间修改,输入 \(N\) \(u\) \(v\) 将 \(u,v\) 节点之间的边权都变为相反数,用布尔数组 \(c[k]\) (懒标记)记录k区间内是否要被修改,每次修改 \(c[k]\)\(^\)$ =1$;
-
操作3:区间询问,输入 \(SUM\) \(u\) \(v\) 询问 \(u,v\) 节点之间边权和
-
操作4:区间询问,输入 \(MAX\) \(u\) \(v\) 询问 \(u,v\) 节点之间边权最大值
-
操作5:区间询问,输入 \(MIN\) \(u\) \(v\) 询问 \(u,v\) 节点之间边权最小值
\(\quad\)其他就是一些细节方面的问题了,比如取反时 \(sum[k]=-sum[k]\),\(Min[k]=-Max[k]\),\(Max[k]=-Min[k]\)
il void change(int k,int l,int r)
{
int m1=Min[k],m2=Max[k];
sum[k]=-sum[k];Min[k]=-m2;Max[k]=-m1;c[k]^=1;
}
接下来就是完整\(AC\)代码了
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
using namespace std;
#define next neee
#define re register int
#define il inline
#define inf 1e18
il int read()
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)&&ch!='-')ch=getchar();
if(ch=='-')f=-1,ch=getchar();
while(isdigit(ch))x=(x<<1)+(x<<3)+ch-'0',ch=getchar();
return x*f;
}
il void print(int x)
{if(x<0)putchar('-'),x=-x;if(x/10)print(x/10);putchar(x%10+'0');}
const int N=2e5+5;
int n,m,next[N<<1],go[N<<1],head[N],tot,s[N<<1],a[N],Min[N<<2],top[N];
int sum[N<<2],Max[N<<2],seg[N],rev[N],son[N],size[N],dep[N],father[N];
bool c[N<<2];
il void Add(int x,int y,int z)//链式前向星存图
{next[++tot]=head[x];head[x]=tot;go[tot]=y;s[tot]=z;}
//------------预处理---------------------------
il void dfs1(int x,int fa,int ss)//第一次dfs处理数组father,son,dep,size,a
{
father[x]=fa;dep[x]=dep[fa]+1;size[x]=1;a[x]=ss;//ss表示x与fa(x的父亲)的连边的权值
for(re i=head[x],y;i,y=go[i];i=next[i])
{
if(y==fa)continue;
dfs1(y,x,s[i]);
size[x]+=size[y];
if(size[y]>size[son[x]])son[x]=y;
}
}
il void dfs2(int x,int topf)//第二次dfs处理数组top,seg,rev
{
top[x]=topf;seg[x]=++seg[0];rev[seg[x]]=x;
if(!son[x])return;
dfs2(son[x],topf);
for(re i=head[x],y;i,y=go[i];i=next[i])
{
if(top[y])continue;
dfs2(y,y);
}
}
il void build(int k,int l,int r)//建树
{
if(l==r){Min[k]=Max[k]=sum[k]=a[rev[l]];return;}
int mid=l+r>>1;
build(k<<1,l,mid);build(k<<1|1,mid+1,r);
Min[k]=min(Min[k<<1],Min[k<<1|1]);
Max[k]=max(Max[k<<1],Max[k<<1|1]);
sum[k]=sum[k<<1]+sum[k<<1|1];
}
//------------预处理---------------------------
//------------线段树---------------------------
il void change(int k,int l,int r)//取反操作
{int m1=Min[k],m2=Max[k];sum[k]=-sum[k];Min[k]=-m2;Max[k]=-m1;c[k]^=1;}
il void pushdown(int k,int l,int r,int mid)//下传标记
{if(l==r){c[k]=0;return;}change(k<<1,l,mid);change(k<<1|1,mid+1,r);c[k]=0;}
il void change1(int k,int l,int r,int x,int y)//单点修改
{
if(l==r){Min[k]=Max[k]=sum[k]=y;return;}
int mid=l+r>>1;
if(c[k])pushdown(k,l,r,mid);
if(x<=mid)change1(k<<1,l,mid,x,y);
else change1(k<<1|1,mid+1,r,x,y);
Min[k]=min(Min[k<<1],Min[k<<1|1]);
Max[k]=max(Max[k<<1],Max[k<<1|1]);
sum[k]=sum[k<<1]+sum[k<<1|1];
}
il void change2(int k,int l,int r,int x,int y)//区间取反
{
if(x<=l&&y>=r){change(k,l,r);return;}
int mid=l+r>>1;
if(c[k])pushdown(k,l,r,mid);
if(x<=mid)change2(k<<1,l,mid,x,y);
if(y>mid)change2(k<<1|1,mid+1,r,x,y);
Min[k]=min(Min[k<<1],Min[k<<1|1]);
Max[k]=max(Max[k<<1],Max[k<<1|1]);
sum[k]=sum[k<<1]+sum[k<<1|1];
}
il int query(int k,int l,int r,int x,int y,int z)//区间询问
{
if(x<=l&&y>=r){
if(z==1)return sum[k];//z==1-->>求SUM
if(z==2)return Max[k];//z==2-->>求MAX
return Min[k];} //z==3-->>求MIN
int mid=l+r>>1,res;
if(c[k])pushdown(k,l,r,mid);
if(z==1){res=0;if(x<=mid)res+=query(k<<1,l,mid,x,y,z);if(y>mid)res+=query(k<<1|1,mid+1,r,x,y,z);return res;}
if(z==2){res=-10000;if(x<=mid)res=max(res,query(k<<1,l,mid,x,y,z));if(y>mid)res=max(res,query(k<<1|1,mid+1,r,x,y,z));return res;}
res=10000;if(x<=mid)res=min(res,query(k<<1,l,mid,x,y,z));if(y>mid)res=min(res,query(k<<1|1,mid+1,r,x,y,z));return res;
}
//------------线段树--------------------------
//------------树链剖分------------------------
il void change3(int x,int y)
{
int xx=go[x<<1],yy=go[(x<<1)-1];
if(xx==father[yy])change1(1,1,n,seg[yy],y);
else change1(1,1,n,seg[xx],y);
}
il void change4(int x,int y)
{
int fx=top[x],fy=top[y];
while(fx!=fy){
if(dep[fx]<dep[fy])swap(x,y),swap(fx,fy);
change2(1,1,n,seg[fx],seg[x]); //链顶在前
x=father[fx];fx=top[x];
}
if(dep[x]>dep[y])swap(x,y);
if(seg[x]+1<=seg[y])change2(1,1,n,seg[x]+1,seg[y]);//记得seg[x]+1
}
il int query1(int x,int y,int z)
{
int fx=top[x],fy=top[y],res;
if(z==1)res=0;
else if(z==2)res=-10000;
else if(z==3)res=10000;
while(fx!=fy)
{
if(dep[fx]<dep[fy])swap(x,y),swap(fx,fy);
if(z==1)res+=query(1,1,n,seg[fx],seg[x],z);
else if(z==2)res=max(res,query(1,1,n,seg[fx],seg[x],z));
else if(z==3)res=min(res,query(1,1,n,seg[fx],seg[x],z));
x=father[fx];fx=top[x];
}
if(dep[x]>dep[y])swap(x,y);
if(seg[x]==seg[y])return res;
if(z==1)res+=query(1,1,n,seg[x]+1,seg[y],z);//最后一次询问是seg[x]+1到seg[y]
if(z==2)res=max(res,query(1,1,n,seg[x]+1,seg[y],z));//最后一次询问是seg[x]+1到seg[y]
if(z==3)res=min(res,query(1,1,n,seg[x]+1,seg[y],z));//最后一次询问是seg[x]+1到seg[y]
return res;
}
//------------树链剖分------------------------
signed main()
{
n=read();
for(re i=1;i<n;i++)
{re x=read()+1,y=read()+1,z=read();Add(x,y,z);Add(y,x,z);}
m=read();
dfs1(1,0,0);dfs2(1,1);build(1,1,n);//树链剖分预处理
string s1;
while(m--)
{
cin>>s1;re x=read()+1,y=read()+1,z=0;
if(s1=="C"){change3(x-1,y-1);continue;}
if(s1=="N"){change4(x,y);continue;}
if(s1=="SUM")z=1;else if(s1=="MAX")z=2;else if(s1=="MIN")z=3;
print(query1(x,y,z));putchar('\n');
}
return 0;
}
\(\quad\)写题解不易,如果觉得对您有帮助,不妨点个赞吧!


