<数论>逆元
逆元
概念
逆元：逆元在数学的不同分支里有不同的定义，这边初略介绍逆元的定义(a/b)%mod=(a*k)%mod。
这里k为inv(b)，称为b的逆元,存在的条件是b和mod互质。
应用
逆元到底有什么用呢？？？
我们都知道
但是……当乘号变为除号也适用吗？？
答案是否定的，所以我们就可以利用逆元去解决这个问题
(a/b)%mod=(a*inv(b))%mod=(a%mod* (inv(b)%mod)%mod 这样就能顺利取模啦~
所以我们如何去求inv(b)呢？
逆元的求法
1、费马小定理推论式
推论式：
mod为素数时，(a/b)%mod=a*(b)^(mod-2)%mod
这个推论式可以很好的解决除法取模的问题
实战分析：http://www.xujcoj.org/Home/Contest/problem/cid/758/match_id/12/ctype/1
题意：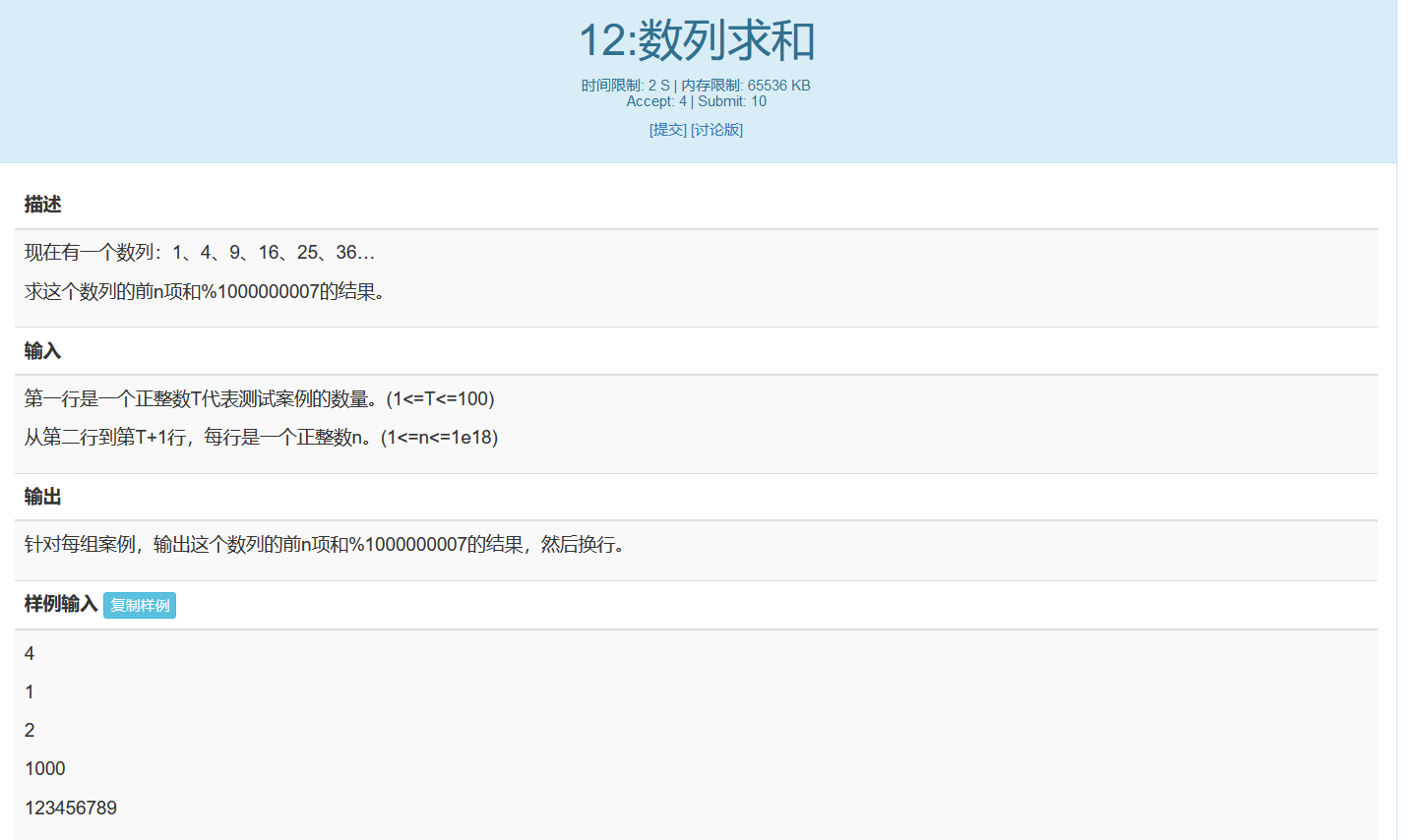
首先小学二年级就知道的自然数平方级数的求和通项公式为
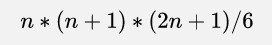
由于mod为质素，所以我们利用上述公式得到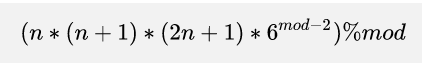
再根据取模运算性质得到
(错误公式 思考一下为什么~)
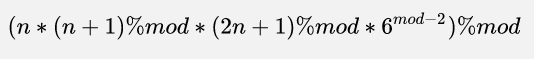
(正确公式)
Ps: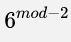
这一块利用快速幂取模~
快速幂:
ll qp(ll b, ll p)
{
ll ans = 1;
while (p)
{
if (p & 1)
{
ans = (ans * b) % mod;
}
b = (b * b) % mod;
p >>= 1;
}
return ans;
}
下面附上ac代码：
int main()
{
ll n, t;
cin >> t;
while (t--)
{
cin >> n;
cout << (((n % mod *((n + 1) % mod)) % mod * ((2*n + 1) % mod) % mod) % mod * qp(6, mod - 2)% mod)%mod << endl;
}
}
对公式用函数优化后：
ll m(ll a, ll b)
{
return (a % mod) * (b % mod) % mod;
}
int main()
{
ll n, t;
cin >> t;
while (t--)
{
cin >> n;
cout << m(m(m(n, n + 1), 2 * n + 1), qp(6, mod - 2)) << endl;
}
}
