线性三角化法 Triangulate

定义：slam中的三角测量指通过不同位置观测一个三维空间中特征点的夹角，从而测得点的深度值；同理亦可通过三角化恢复二维特征点的三维坐标，单目情况下由于平移t尺度的不确定性只能恢复相对三维坐标。

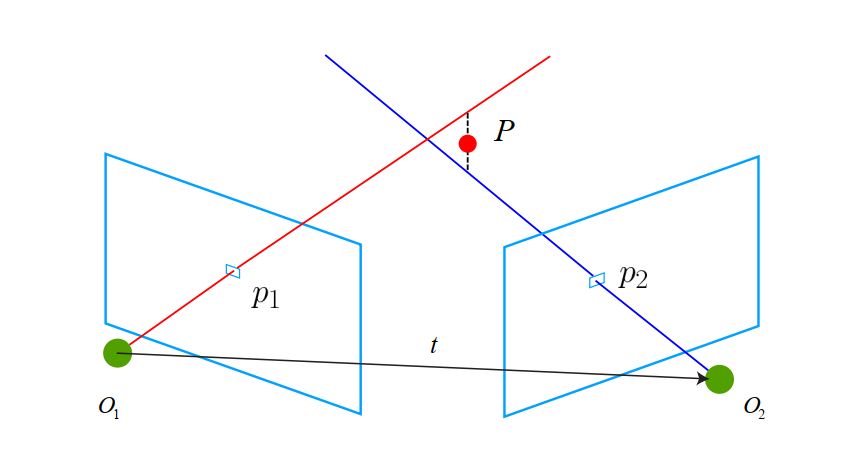
考虑图像 I1 和 I2，以左图为参考，右图的变换矩阵为 T。相机光心为 O1 和 O2。在 I1 中有特征点 p1，对应 I2 中有特征点 p2。理论上直线 O1p1 与 O2p2 在场景中会相交于一点 P，该点即是两个特征点所对应的地图点在三维场景中的位置。

然而由于噪声的影响，这两条直线往往无法相交 因此，也可以通过最二小乘去求解。

 

---

方法：

目标：在此使用DLT恢复$p_1$  ,$p_2$  对应的三维坐标 X；

已知：相机内参K ，外参$T_1$，$T_2$  三维点P对应的图像点$p_1$  ,$p_2$像素坐标$x_1=\begin{pmatrix}u_1\\v_1\\1\end{pmatrix}$  ,$x_2=\begin{pmatrix}u_2\\v_2\\1\end{pmatrix}$；

 

相机矩阵 $P=KT$        其中  $K 3 \times3$  ,    $T=[R|t]  3\times4$  ;

像素坐标 $x_1=KT_1X=P_1X$;

　　　　$x_2=KT_2X=P_2X$;

通过叉乘消去纯量因子，使每个图像点得到三个方程，其中两个是线性独立的，对于第一幅图像有；

$x_1^{\wedge}x_1=x_1^{\wedge}PX=0$

其中 $x_1^{\wedge}=\begin{pmatrix}0&-1&v_1\\1&0&-u_1\\-v_1&u_1&0\end{pmatrix}$

展开得

$u_1\left(P^3_1X\right)-\left(P^1_1X\right)=0$

$v_1\left(P^3_1X\right)-\left(P^2_1X\right)=0$

$u_1\left(P^2_1X\right)-v_1\left(P^1_1X\right)=0$

其中$P^1$ 是P的行，这些关于X的分量是线性的；

 

同理对于第二幅图像也可以得到三个方程；

 

各取两个方程得到四个齐次未知量为四的方程，组成$AX=0$的方程；

$A=\left(\begin{array}{cc}{u_{1} P_{1}^{3}} & {-P_{1}^{1}} \\ {v_{1} P_{1}^{3}} & {-P_{1}^{2}} \\ {u_{2} P_{2}^{3}} & {-P_{2}^{1}} \\ {v_{2} P_{2}^{3}} & {-P_{2}^{2}}\end{array}\right)$

通过SVD解 $AX=0$  得到X

 

---

代码

**
 * @brief 给定投影矩阵P1,P2和图像上的点kp1,kp2，从而恢复3D坐标
 *
 * @param kp1 特征点, in reference frame
 * @param kp2 特征点, in current frame
 * @param P1  投影矩阵P1
 * @param P2  投影矩阵P２
 * @param x3D 三维点
 * @see       Multiple View Geometry in Computer Vision - 12.2 Linear triangulation methods p312      chinese 218
 */
void Initializer::Triangulate(const cv::KeyPoint &kp1, const cv::KeyPoint &kp2, const cv::Mat &P1, const cv::Mat &P2, cv::Mat &x3D)
{
    // 在DecomposeE函数和ReconstructH函数中对t有归一化
    // 这里三角化过程中恢复的3D点深度取决于 t 的尺度，
    // 但是这里恢复的3D点并没有决定单目整个SLAM过程的尺度
    // 因为CreateInitialMapMonocular函数对3D点深度会缩放，然后反过来对 t 有改变

    cv::Mat A(4,4,CV_32F);

    A.row(0) = kp1.pt.x*P1.row(2)-P1.row(0);
    A.row(1) = kp1.pt.y*P1.row(2)-P1.row(1);
    A.row(2) = kp2.pt.x*P2.row(2)-P2.row(0);
    A.row(3) = kp2.pt.y*P2.row(2)-P2.row(1);

    //Ax=0
    cv::Mat u,w,vt;
    cv::SVD::compute(A,w,u,vt,cv::SVD::MODIFY_A| cv::SVD::FULL_UV);
    x3D = vt.row(3).t();//竖排
    x3D = x3D.rowRange(0,3)/x3D.at<float>(3);//齐次  尺度变换成1
}