信息熵

 

定义：信息熵是用来描述某个事情发生概率所带来的信息量（影响）

描述：

我们倾向于认为加法比乘法友好，简单 

独立事件x,y 发生的概率

P(x,y)=P(x)P(y)   两边取对数-> lnP(x,y)=lnP(x) + lnP(y)  

 

我们认为可能性小的事情发生带来的信息量会更大，比如中国男足取得世界冠军和中国兵兵球世界冠军带来的影响是完全不一样的。即为减函数

ln() 在0~1 上是增函数 ->  -ln() 减函数

 

X    　 　  1      　  2   　　 3     　 4

P　　　　 0.1 　　0.6　　 0.2　　 0.1

 

-lnP() -ln(0.1) -ln(0.6) -ln(0.2) -ln(0.1)

 

信息熵 H(x)=  -(0.1ln(0.1)+0.6ln(0.6)+0.2ln(0.2)+0.1ln(0.1))

-ln(0.1) 虽然很大 但是发生概率很低0.1 -->-0.1ln(0.1)

 

 $H(X)=-\sum_{x \in X} p(x) \ln p(x)$

 

注：

金典熵底数为2 ，单位bit

方便分析用底数e,单位nat(奈特）

 

欧拉方式

X   0   1

P   1-p  p

 

两点分布信息熵 ： H(p)=  -(1-p)ln(1-p)-pln(p)

 

import numpy as np
import matplotlib.pyplot as plt

esp=1e-4
p=np.linspace(esp,1-esp,100)
h=-(1-p)*np.log(1-p) -p*np.log(p)

plt.plot(p,h,'-r',lw=3)
plt.show()

 

 

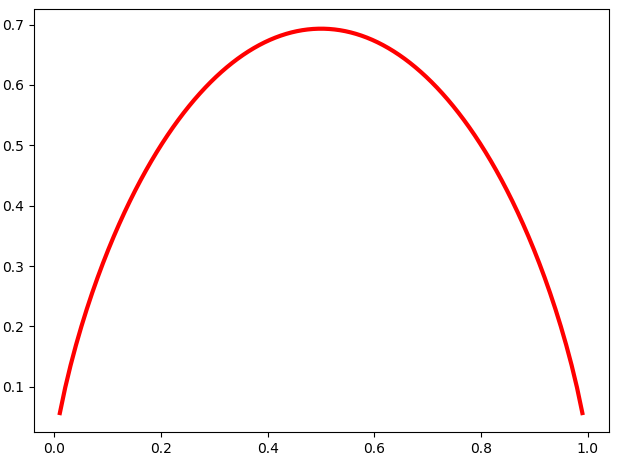
完全确定事件带来的信息熵为0   

明天太阳从西北升起 -> 不可能事件 p=0  -> h=0

 

同理也有三点熵四点熵。。。。。

 

 

关于熵的其他想法

无外界干扰下熵变化的趋势总是增大的 -> 趋于不确定方向 -> 混乱      即      减小熵 -> 需要外界力量

 

---

 

信息增益

 

gain(Y,X) = H(Y) - H(Y|X)

在决策树过程中判断划分的效果依据是添加条件后熵又没降低

 

根节点   熵：1.582 |   数量：105

左孩子  熵：0.657  |   数量：38      右孩子  熵：1.208  |   数量：67 

H(Y|X)=(38/105 ) *1.582 +  (67 /105)  *1.208 = 1.009    ；        H(Y|X)------ 条件熵

H(Y)=1.582  ；

H(Y) - H(Y|X)=0.573   ； -> 熵降低 -> 不确定程度降低 -> 确定性程度提高了

 

gain(Y,X) = H(Y) - H(Y|X)  ；遍历选择不同的X使得gain(Y,X)信息增益最大，效果最好 ，这里选择，

 

 

50min-*************************************************************