2/19 福建四校联考

1.设计图案

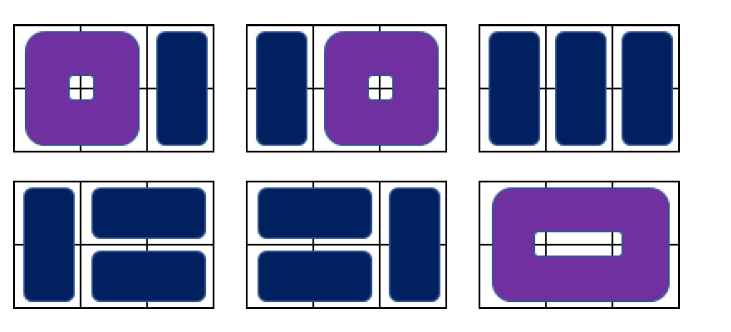
给你一个n*m的矩阵，每个格子必须填或者不能填，要用环和1*2的小方块填满它，求方案数。

比如3*2，每个格子都必须填 有6种填法。

n*m<=300  

当时一看就觉得不可做然后就放弃了.....

题解：有个结论：

 

 

状压dp详细就是：

按照从上到下，从左到右dp，用f[i][j][k]表示到第i行j列的格子，轮廓线之上的格子的状态是k的方案数量。

如果这个格子不能填，那么他上面的格子必须被填满，上面格子也被填了的时候f[i][j][k]=f[i][j-1][k](j!=1)或者f[i-1][m][k](j=1)

如果这个格子可以填，那么先看一下它上面那个格子是否填满了，没填满就一定要填，填满了就不能竖着填了。然后看一下能不能横着填就可以了。

设x=2^(j-1)   f[i][j][k^x]+=f[i][j-1][k](j!=1) 或者f[i-1][m][k](j==1)    这句话表示的是填竖着的。

当j!=1时，判断一下是否可以横着填,可以的时候f[i][j][k|(x<<1)]+=f[i][j-1][k]

复杂度 nm * 2^(min(n,m))

实际实现可以滚动数组，这样简单很多。

代码

#include<iostream>
#include<cstdio>
#define ll long long
#include<cstring>
using namespace std;
inline int read()
{
    int  x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0'; ch=getchar();}
    return x*f;
}
int n,m,mod;
ll f[2][1<<17];
bool b[305][305];
bool b2[305][305];

int main()
{
    freopen("design.in","r",stdin);
    freopen("design.out","w",stdout);
    n=read();m=read();mod=read();
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            b[i][j]=(bool)read();
    if(n<m)
    {
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
                b2[i][j]=b[i][j];
        swap(n,m);
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
                b[i][j]=b2[j][i];
    }
    int nown=1,pre=0,to=(1<<m)-1;
    f[pre][to]=1;
    for(int i=1;i<=n;i++)
    {
         for(int j=1;j<=m;j++)
        {
            for(int k=0;k<=to;k++)
            {
                int x=1<<j-1;
                if(!b[i][j])
                {
                    if((k|x)==k) 
                        f[nown][k]=(f[nown][k]+f[pre][k])%mod;    
                }    
                else
                {
                    f[nown][k^x]=(f[nown][k^x]+f[pre][k])%mod;    
                    if(j!=1&&(k|x)==k&&((k|(x>>1))!=k)&&b[i][j-1])
                        f[nown][k|(x>>1)]=(f[nown][k|(x>>1)]+f[pre][k])%mod;
                }    
            }
            pre=1-pre;nown=1-nown;memset(f[nown],0,sizeof(f[nown]));        
        }  
    }
    ll ans=(f[pre][to]*f[pre][to])%mod; 
    printf("%lld\n",ans);
    return 0;
}

 

 2.最优发射

大意：有一个环，有n个武器，每个武器可以打死一个区间内的人。

多组数据，每次给你很多人，问至少要多少个武器可以全部打死.....

n<=100000  人的总数<=200000

题解做法：

倍增加速贪心。

我的做法：

先删掉没用的边，这样的话就可以保证边的l和r都是递增的。由于数据组数比较多，所以显然不能每次遍历全部边。每个点直接二分一个能盖住它的边中最右能到哪里。

不考虑环，显然是一个dp，可以优化到nlogn  

但是加上环之后就比较麻烦，可以用一个lct维护一下dp路径

从1到m遍历，从每一个点向它能转移的点连边，如果它能越过环，就向m+1连边，这样的话一个点的深度就是它一直到现在的点的dp值。

每个点如果有能跨过环的边，那么就用能跨到的地方右边的第一个点的深度+1更新一下答案。

复杂度nlogn

现场的时候写挂了只有60.

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#define INF 2000000000
#define ms(x) memset(x,0,sizeof(x))
using namespace std;
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0'; ch=getchar();}
    return x*f;
}
int n,m,L,qq,ans;
int t[400005];
int c[200005][2];
int fa[200005],size[200005];
int rev[200005];
int qu[200005],top=0;
int tf[200005];
bool yes;

struct line{
    int l,r;
}ll[400005];

bool cmp(line x,line y)
{
    return (x.l<y.l)||(x.l==y.l&&x.r>y.r);
}

inline bool isroot(int x){return c[fa[x]][0]!=x&&c[fa[x]][1]!=x;}
inline void update(int x){size[x]=size[c[x][0]]+size[c[x][1]]+1;}

void rotate(int x)
{
    //printf("rotate%d\n",x);
    int y=fa[x],z=fa[y],l,r;
    l=(c[y][1]==x),r=l^1;
    if(!isroot(y)) c[z][c[z][1]==y]=x;
    fa[x]=z;fa[y]=x;fa[c[x][r]]=y;
    c[y][l]=c[x][r];c[x][r]=y;
    update(y);update(x);
}

void splay(int x)
{
    while(!isroot(x))
    {
        int y=fa[x],z=fa[y];
        if(!isroot(y))
        {
            if(c[z][1]==y^c[y][1]==x)rotate(x);
            else rotate(y);
        }
        rotate(x);
    }
}

void access(int x)
{
    splay(x);
    while(fa[x])
    {
        int y=fa[x];splay(y);
        c[y][1]=x;
        update(y);splay(x);
    }
}
void link(int x,int y)
{
    access(x);splay(x);
    //rever(c[x][0]);
    access(y);splay(y);
    c[y][1]=x;fa[x]=y;
}

void cut(int x)
{
    access(x);splay(x);fa[c[x][0]]=0;c[x][0]=0;
}


int get(int x)
{
    int l=1,r=n,mid,ans=-1;
    while(l<=r)
    {
        mid=(l+r)>>1;
        if(ll[mid].l>x) r=mid-1;
        else
        {    
            ans=ll[mid].r;
            l=mid+1;    
        }    
    }
    return ans;
}

int get2(int x)
{
    int l=1,r=m,mid,ans=0;
    while(l<=r)
    {
        mid=(l+r)>>1;
        if(t[mid]<=x) {ans=mid;l=mid+1;}
        else {r=mid-1;}
    }
    return ans;
}

int check(int x)
{
    access(x);//splay(x);
    return size[c[x][0]];
}

int main()
{
    freopen("launch.in","r",stdin);
    freopen("launch.out","w",stdout);
    n=read();qq=read();L=read();
    for(int i=1;i<=n;i++)
    {
        ll[i].l=read();ll[i].r=read();
        if(ll[i].r<ll[i].l) ll[i].r+=L;
    }
    for(int i=1;i<=n;i++) if(ll[i].r>=L) 
    {
        ll[++n].l=0;
        ll[n].r=ll[i].r-L;    
    }
    sort(ll+1,ll+n+1,cmp);
    int j=1;
    for(int i=2;i<=n;i++)
    {
        if(ll[i].r>ll[j].r) 
        {ll[++j]=ll[i];}     
    }    
    n=j;
//    for(int i=1;i<=n;i++) printf("%d %d %d\n",i,ll[i].l,ll[i].r);
    while(qq--)
    {
        ms(fa);ms(c);ms(size);ms(rev);t[0]=-1;
        yes=true;m=read();for(int i=1;i<=m;i++) t[i]=read();
        sort(t+1,t+m+1);ans=INF;size[m+1]=1;
        int j=1;
        for(int i=2;i<=m;i++)
            if(t[i]!=t[j]) t[++j]=t[i];
        m=j;
        for(int i=0;i++<=m;i++) size[i]=1;
        if(yes) for(int i=1;i<=m;i++)
        {
            int x=get(t[i]);
            if(x==-1||x<t[i]) {puts("-1");yes=false;break;}
            if(x-L>=t[1])
            { 
                ans=min(ans,check(get2(x-L)+1)+1);
                link(i,m+1);
            }
            else 
                link(i,get2(x)+1);
        }
        ans=min(ans,check(1));
        if(yes) printf("%d\n",ans);
    }
    return 0;    
}

 

 3.传输网络

有m条信息，n个传输装置。

每个装置可以把一个范围a-b内的全部信息转移到c（a<=c<=b），但是需要d点费用

现在要把全部信息都转移到一个点，求最小费用。

m<=10^9 n<=10^5

先离散一下，再用两个线段树维护第一条和最后一条信息到每个点c的距离。

然后按dp做就行了。

现场只写了n^3 dp 只有50分......

#include<iostream>
#include<cstdio>
#include<algorithm>
#define ll long long
#define N 262144
#define INF 1000000000000000000LL
using namespace std;
inline ll llread()
{
    ll x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0'; ch=getchar();}
    return x*f;
}
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0'; ch=getchar();}
    return x*f;
}
int n,m,cnt=0;
ll ans=INF;
int s[300005];
struct ma{
    int l,r,c;
    ll d;
}a[100005];

ll T1[600005],T2[600005];

ll query(ll*T,int l,int r)
{
    ll minn=INF;
    for(l+=N-1,r+=N+1;l^r^1;l>>=1,r>>=1)
    {
        if(~l&1) minn=min(minn,T[l+1]);
        if( r&1) minn=min(minn,T[r-1]);    
    }
    return minn;
}

void renew(ll*T,int x,ll ad)
{
    T[x+=N]=min(T[x],ad);
    for(x>>=1;x;x>>=1)
       T[x]=min(T[x<<1],T[(x<<1)+1]);    
} 

void init()
{
    for(int i=1;i<=N*2;i++)
        T1[i]=T2[i]=INF;
}

int main()
{
    freopen("network.in","r",stdin);
    freopen("network.out","w",stdout);
    n=read();m=read();
    for(int i=1;i<=n;i++)
    {
        a[i].l=read();
        a[i].r=read();
        a[i].c=s[i]=read();
        a[i].d=llread();
    }
    s[n+1]=1;
    s[n+2]=m;
    sort(s+1,s+n+3);init();
    int j=0;
    for(int i=1;i<=n+2;i++)
    {
        if(s[i]!=s[i-1])
           s[++j]=s[i];
    }cnt=j;
    renew(T1,1,0);renew(T2,cnt,0);
    for(int i=1;i<=n;i++)
    {
        a[i].l=lower_bound(s+1,s+cnt+1,a[i].l)-s;
        a[i].r=upper_bound(s+1,s+cnt+1,a[i].r)-s-1;
        a[i].c=lower_bound(s+1,s+cnt+1,a[i].c)-s;
    }
    for(int i=1;i<=n;i++)
    {
        if(a[i].l>a[i].r||a[i].l>cnt||a[i].r>cnt) continue;
        ll x1=query(T1,a[i].l,a[i].r);
        ll x2=query(T2,a[i].l,a[i].r);
        ans=min(ans,x1+x2+a[i].d);
        renew(T1,a[i].c,x1+a[i].d);
        renew(T2,a[i].c,x2+a[i].d);    
    }
    if(ans<INF) printf("%lld\n",ans);
    else puts("-1");
    return 0;
}