[图形学][转载]圆心角和圆周角相关问题，补充相关解答

转自：http://blog.csdn.net/silangquan/article/details/18450199

题目：两圆相交，只有2交点A、B，过A点做线段CAD，CA、AD为两圆的弦，问什么情况下CAD最长，并证明。提示圆心角和圆周角的两倍关系。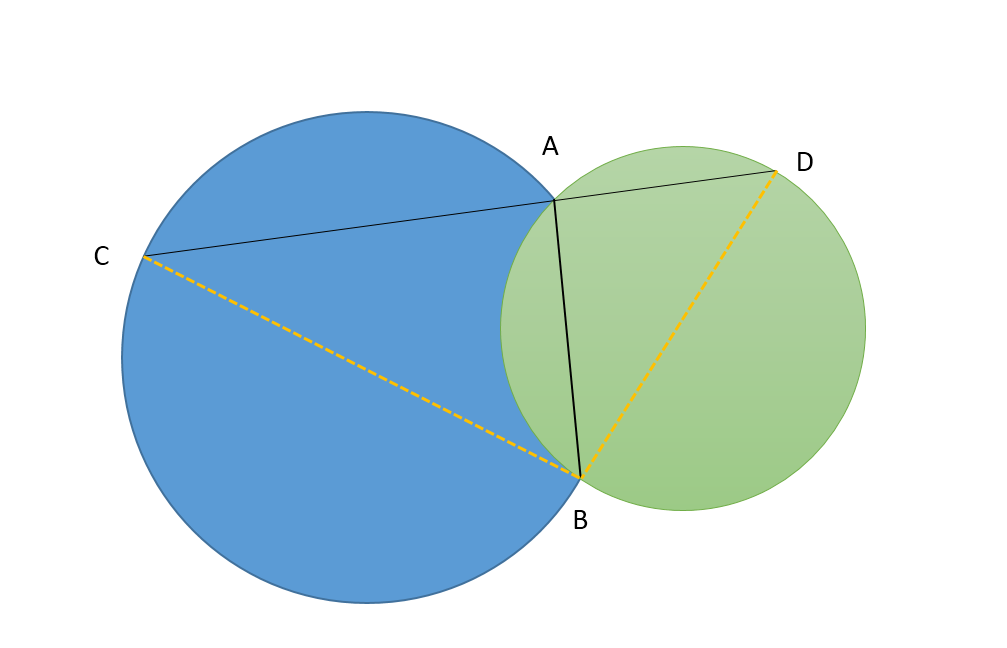

如图分别连接BC，BD。

当CAD不断的变化的时候，可以得到个无数个三角形CBD。

这些三角形的夹BCA和角BDA都是相同的，分别是BA对应的圆心角的一半，因为BCA和BDA无论怎么变化角度都不变,则这些三角形都是相似的。

根据相似三角形的性质，三边成比例，多个相似三角形，最小边BD最大的情况下，其余的边如BC和CD也是最大。

那么当BD最大的时候，也就是三角形最大的时候，也就是CD最长的时候。

BD最大的时候就是BD为圆的直径，则BAD为直角，同理，BAC也是直角=>BA 垂直CAD。