我真的是太太太太蒟蒻了QwQ

2020/8/25晚

Lcy大佬让我们进了QHOI洛谷群，然后就让我们AK掉他一年前搞的比赛
然后别人就一个又一个AC了T1（lcy说这是**题）QAQ结果我A不掉.....
不过确实不是很难，没有考到算法，完全是数学Problem（太菜了，数学都不会了QWQ

题目

先亮 简单 题

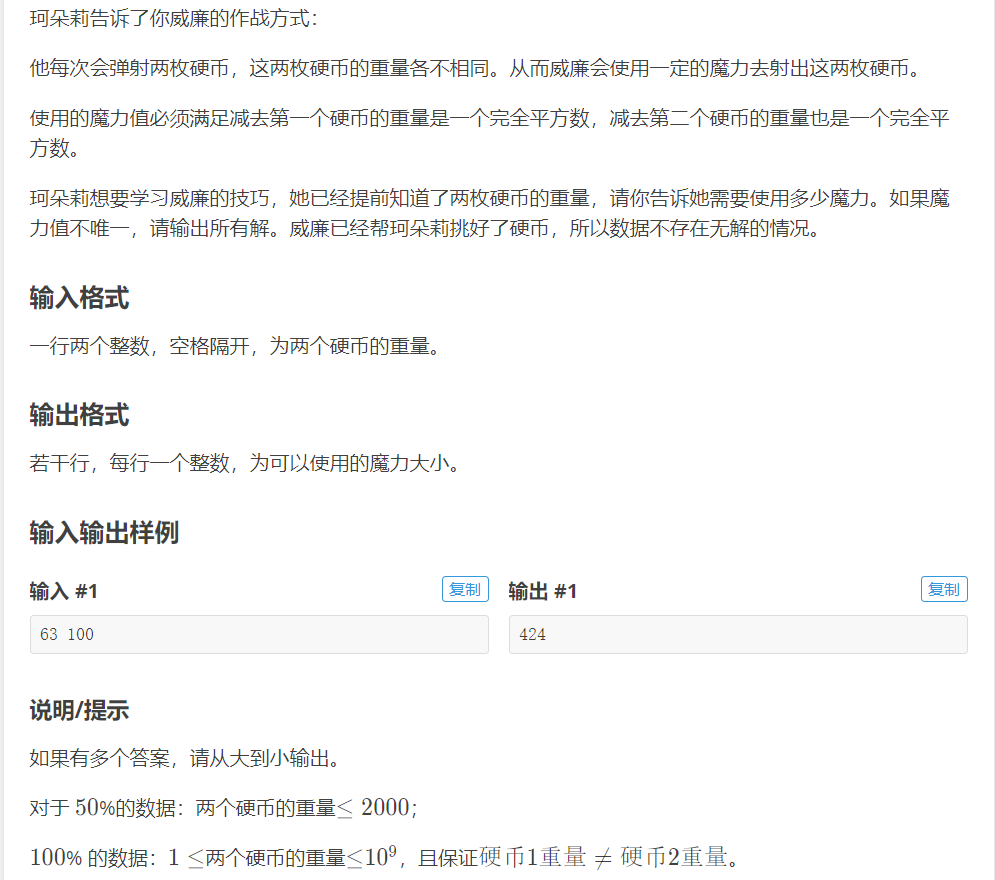
先不管前面的可爱的珂朵莉了，先把题给A了，题目可以理解为：
对于正整数\(a\),\(b\),要找到满足\((k-a)\)和\((k-b)\)都是完全平方数的所有\(k\)，并从大到小输出

思路

-首先肯定会想到暴力枚举并处理，结果是爆零！大佬数据太牛了（或者是我太弱啦，lcy说这题他小学觉得有点难，orz

然后通过长时间的找规律加以思考，有了如下思路：
设

\(sqrt(k-a)=p\)，\(sqrt(k-b)=q\)，

则有

\(p^2+a=q^2+b=k\)，

即

\(p^2-q^2=abs(b-a)(a>b)\)，

整理可得

\((p+q)(p-q)=a-b\)，

此时的话，\(k\)应该是\(p^2+a\)或者是与之相同的\(q^2+b\)。

可是然后呢？？？本蒟蒻当时只能想到这了，不会求了，还是26号让大佬和我讲讲吧(希望能听懂—_—)

正解

（次日，lcy跟我解释完了，前面的思路是没错，然后就是该想以下内容了。
首先已知\(a\),\(b\)都是正整数，那么它们的差值的绝对值自然也是非负整数，那么可以将这个差值进行优化的找因子，只要到\(logn\)即可（具体看代码。

每找到一个因子\(m\)，就可以使\(n=(a-b)/m\)，从而\(nm=a-b=(p+q)(p-q)\)。

由于只需找到\(sqrt(n)\)，自然所找到的因子\(m\)都会小于\(n\)，比如对于数字8，只会找到2，不可能到4。这个也很好想，不赘述了QAQ

那么对于式子\((p-q)(p+q)\)而言，显而易见，\(p-q<p+q(p,q\in N*)\)，所以可以有\(m=p-q,n=p+q\)，

解得 \(p=(m+n)/2,q=n-p\)。

但是这里又有一些小问题，如果解出来的\(p\)是小数，那么这组解是不是正解呢？？？

肯定不是啦！回翻到题目，你会看到这一句话：

\((k-a)\)和\((k-b)\)都是完全平方数

再翻到思路，你又会看到这一句话：

\(sqrt(k-a)=p\)，\(sqrt(k-b)=q\)

这不就说明了\(p,q\)都是正整数了吗？

贴代码

void solve(ll x,ll y){
	ll p,q;
	if(x>y)swap(x,y);
	ll cha=abs(x-y);
	for(register int i=1;i*i<=cha;++i){
		if(cha%i==0&&(i+cha/i)%2==0){
			//p-q=i;p+q=cha/i;
			p=(i+cha/i)/2;//大的 
			q=p-i;//小的 
			cout<<p*p+x<<endl;
		}
	}
}

完整代码

#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll a,b;
void solve(ll x,ll y){
	ll p,q;
	if(x>y)swap(x,y);
	ll cha=abs(x-y);
	for(register int i=1;i*i<=cha;++i){
		if(cha%i==0&&(i+cha/i)%2==0){
			//p-q=i;p+q=cha/i;
			p=(i+cha/i)/2;//大的 
			q=p-i;//小的 
			cout<<p*p+x<<endl;
		}
	}
}
int main(){
	cin>>a>>b;
	solve(a,b);
	return 0;
}
/*
今天你AC了几题?
不要颓废！！！！
Dalao has AKed IOI several times!!!
*/

结果

芜湖，完美结束这道题了！QwQ