常用校验码(奇偶校验,海明校验,CRC)学习总结
常用校验码(奇偶校验,海明校验,CRC)学习总结
一.为什么要有校验码?
因为在数据存取和传送的过程中,由于元器件或者噪音的干扰等原因会出现错误,这个时候我们就需要采取相应的措施,发现并纠正错误,对于错误的检测和校正,大多采取“冗余校验”的思想,即除原数据外,额外增加若干位编码,这些新增的代码称为校验位。
二.数据是如何校验的?

- 输入的数据m经过f得到p校验位。
- 数据m和校验位一起通过存储器或传输线路,分别得到m'和p',这两者可能和m,f相同,也可能由于传输储存发生问题而不同。
- 由数据m'再次经过f得到校验位p'',比较p''和p',从而得出是否出错,输出对应的信息,如何比较,会在下面的对应校验码中给出。
三.码距
若干位代码组成的一个字称为码字,而两个码字具有不同代码的位数为这两个码字的距离,而码制里各种码字间最小的距离称为码距。
比如8421码,1001和0000,有两位不同,所以距离是2,而0010和0011的距离为1,是最小的距离,故8421码码距为1
那么,码距有什么用呢?答案是码距和这种类型的码的检错,纠错能力有关。
如8421码,由于码距是1,无检错,纠错能力,比如数据0000,如果其中一位变化,变成0001,那么,这个数据仍然是合法的。
再如奇偶校验码中奇校验码,如100000000和010000000,码距为2,我们可以发现,如果数据中有一位变化了,如100000000变为110000000,我们可以很容易地判断出数据出错了,因为110000000不符合奇校验的编码(校验位和数据位一起所含1的个数为奇数)
我们可以发现,校验码可以帮助扩大码距,从而找出错误。
码距与检错、纠错能力的关系(当d≤4)
- 若码距d为奇数,则能发现d-1位错,或能纠正(d-1)/2位错。
- 若码距d为偶数,则能发现d/2位错,并能纠正(d/2-1)位错。
四.奇偶校验码
1.编码方式
- 无论数据位多少位,校验位只有一位
- 数据位和校验位一共所含的1个数为奇数,称为奇校验
- 数据位和校验位一共所含的1个数为偶数,称为偶校验
例如(加粗为校验位):
| 数据 | 奇校验的编码 | 偶校验的编码 |
|---|---|---|
| 00000000 | 100000000 | 000000000 |
| 01010100 | 001010100 | 101010100 |
| 01111111 | 001111111 | 101111111 |
由于数据传输过程一般是出现一位错误,而奇偶校验码能发现奇数个错误,所以奇偶校验的实用价值还是很高的。
2.实现原理
那么,奇偶校验是怎么来发现错误的呢?根据二.数据是如何校验的我们可以知道,在数据传输之前,我们会求一次校验位,传输后,会求一次校验位,那么,在奇偶校验中,我们通过比较这两个校验位是否相同,一般是采用异或的方式,若结果为1,则说明有奇数个错误,结果为0,则说明正确或者偶数个错误。
五.海明校验码
1.引入
- 在了解了奇偶校验码之后,我们可以稍稍做下思考,既然奇偶校验码具有一定的局限性,也就是只能检测奇数的错误,并且不能改正错误,这也就意味着数据一旦传输错误,我们必须要重新上传,那么,我们有办法确定错误发生的位置么?只要确定了错误发生的位置,改正其实就是取反。
- 这个时候,让我们来看看奇偶校验码,它是在数据的前面或者后面加上以为校验位,那么,如果我们将数据分段,分成某些小段,这样是不是能判断错误发生的位置呢?
2.海明校验码 最简单求法
我们以8位数据位,4(5)位校验位为例
我们将海明校验码表示为(H13) H12 H11 H10 H9 H8 H7 H6 H5 H4 H3 H2 H1
其中加粗的部分为校验位,校验位所在位置为2^(i-1),i=1,2,3...
我们还可以把它写成(P5) D8 D7 D6 D5 P4 D4 D3 D2 P3 D1 P2 P1
其中P代表的是校验位,D代表数据位
| 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | S | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2^0 | D7 | D5 | D4 | D2 | D1 | P1 | S1 | ||||||
| 2^1 | D7 | D6 | D4 | D3 | D1 | P2 | S2 | ||||||
| 2^2 | D8 | D4 | D3 | D2 | P3 | S3 | |||||||
| 2^3 | D8 | D7 | D6 | D5 | P4 | S4 |

我们来看看这个表是怎么画出来的
- 首先数据位和校验位的位置我们通过公式可以得出
- 同列数据位所占的位置对应的行的值之和为列的值。举个例子,如D1,所在列为3,所在行分别为20和21,即1和2,满足式子1+2=3。
校验位的值为同行数据位相异或得到,至于P5,则是由所有数据位和校验位一起异或得到。
3.海明校验码判断修复错误
下面引入一个错误字S的概念
其实错误字S也就是传输前后分别求的校验位的异或值,奇偶校验码只要看一个错误字,而海明校验码则要考虑多个错误字。
S4 ~ S1为全0,说明没错. S4 ~ S1不为全0,说明有错. S5=1说明1位出错,而S5=0说明2位错,不再有效,且不能查出是哪2位出错。
S4~S1的编码值对应的则是出错的海明码位号(不太清楚图表可以返回上面的表格对照):
如1100,对应D8出错
如1011,对应D7出错
如1010,对应D6出错
如1001,对应D5出错......
- Tip:我们通过观察8个数据位4个校验位的海明校验码,发现,若一位出错,则至少有两组校验码的生成收到影响,故我们得到其码距为3,根据码距与检错、纠错能力的关系可以得出该校验码能发现两位错,或修改一位错。
4.校验码位数的确定
前面看完后,一定有人会有疑问,为什么八位数据位我要四位或者五位校验位,三位不行么?六位不行么?那么,请继续看看下面
假定数据位数为n,校验码为k位,则故障字位数也为k位。k位故障字所能表示的状态最多是2K,每种状态可用来说明一种出错情况。
若只有一位错,则结果可能是:
数据中某一位错 (n种可能)
校验码中有一位错 (k种可能)
无错 ( 1 种可能)
假定最多有一位错,则n和k必须满足下列关系:
2^k≥1+n+k, 即:2^k-1≥n+k
所以当数据有8位时,校验码和故障字都应有至少4位。
5.分组方式的选择
看了前面,可能有人会对校验位的位置选择有疑问,为什么要符合公式2^(i-1) i=1,2...?上述的表格为什么要那样写?
首先,我们知道,数据位是和校验位一起被储存的,通过将他们按照某种方式排列成一个n+k的码字,将该码字上的每一位出错位置和故障字的数值建立联系,那么我们就能通过故障字的值来判断哪一位发生了错误
- 如果故障字全为0,则说明没有错误
- 如果故障字有且只有一位为1,则表示是校验位中发生错误,不需要矫正
- 如果故障字中有多位为1,则表示有一个数据位出错,其出错位置由故障字的值来确定
以一个八位的数据为例,该数据有四个校验位,在第二条规则中,我们可以知道,故障字的值为0001,0010,0100,1000这四种情况,对应四个校验位P1,P2,P3,P4发生错误,故我们将这四个校验位分别位于码字的第0001(1),0010(2),0100(4),1000(8)位,按照最后一个规则,将其他多位为1的情况作为八位数据M1-M8发生错误。故数据位M1-M8分别位于码字的第0011(3),0101(5),0110(6),0111(7),1001(9),1010(10),1011(11),1100(12)位,排列为M8M7M6M5P4M4M3M2P3M1P2P1
六.循环冗余码(CRC码)
1.为什么大批量数据不用奇偶校验?
在每个字符后增加一位校验位会增加大量的额外开销;尤其在网络通信中,对传输的二进制比特流没有必要再分解成一个个字符,因而无法采用奇偶校验码。
2.模2运算
在介绍CRC码之前,有必要介绍下计算CRC码必要的模2运算:
模2运算不考虑加法进位和减法借位,上商的原则是当部分余数首位是1时商取1,反之商取0。然后按模2相减原则求得最高位后面几位的余数。这样当被除数逐步除完时,最后的余数位数比除数少一位。这样得到的余数就是校验位。
3.基本思想
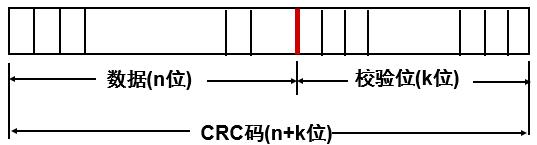
- 数据信息M(x)为一个n位的二进制数据,将M(x)左移k位后,用一个约定的“生成多项式”G(x)相除,G(x)是一个k+1位的二进制数,相除后得到的k位余数就是校验位。校验位拼接到M(x)后,形成一个n+k位的代码,称该代码为循环冗余校验 ( CRC ) 码,也称(n+k,n)码。
- 一个CRC码一定能被生成多项式整除,当数据和校验位一起送到接受端后,只要将接受到的数据和校验位用同样的生成多项式相除,如果正好除尽,表明没有发生错误;若除不尽,则表明某些数据位发生了错误。通常要求重传一次。
4.CRC码求法


5.CRC码检错
将收到的CRC码用约定的生成多项式G(x)去除,如果码字无误则余数应位0,如果有某一位出错,则余数不为0,不同位数出错余数不同.