并查集经典题目
还是先看两道题:
|
试题描述
|
|
俗话说得好,敌人的敌人就是朋友。
现在有n个人,编号1至n,初始互不相识。接下来有m个操作,操作分为两种: (1)检查x号和y号是否是朋友,若不是,则变成敌人(2)询问x号的朋友有多少个 请你针对每个操作中的询问给出回答。 |
|
输入
|
|
第一行两个正整数n、m,表示人的数量和操作的数量。
接下来m行,依次描述输入。每行的第一个整数为1或2表示操作种类。对于操作(1),随后有两个正整数x,y。对于操作(2),随后一个正整数x。 |
|
输出
|
|
输出包含m行,对于操作(1),输入'N'或"Y",'N'表示x和y之前不是朋友,'Y'表示是朋友。对于操作(2),输出x的朋友数量。
|
|
输入示例
|
|
5 8
1 1 2 1 1 3 1 2 3 2 3 1 4 5 2 3 1 1 4 2 3 |
|
输出示例
|
|
N
N Y 1 N 1 N 2 |
|
其他说明
|
|
n,m<=300000。
对于80%的数据,不包含操作2。 |
|
试题描述
|
|
有N只动物分别编号为1,2,……,N。所有动物都属于A,B,C中的一类。已知A能吃掉B,B能吃掉C,C能吃掉A。按顺序给出下面的两种信息共K条: 吕紫剑为学有余力的同学提供了一个提高版,题目链接:http://oj.cnuschool.org.cn/oj/home/problem.htm?problemID=1000(事实上只提高了一点) |
|
输入
|
|
第一行两个自然数,两数间用一个空格分隔,分别表示N和K,接下来的K行,每行有三个数,第一个数为0或1,分别对应第一种或第二种,接着的两个数,分别为该条信息的x和y,三个数两两之间用一个空格分隔。
|
|
输出
|
|
一个自然数,表示错误信息的条数。
|
|
输入示例
|
|
100 7
0 101 1 1 1 2 1 2 3 1 3 3 0 1 3 1 3 1 0 5 5 |
|
输出示例
|
|
3
|
|
其他说明
|
|
数据范围:1<=N<=50000,0<=K<=100000,其它说有输入都不会超过100000.
|
两道并查集的经典题目,现有两种做法可供参考:
先以第一题(名为敌人)为例, 这题和那种并查集的模板题有一点区别,那就是这里多了一种关系:叫做朋友与敌人,如果只有一种关系那就好办了。那怎么处理这多出来的一种关系呢?这里我们先介绍第一种方法,我们管它叫精神分裂法(又称分身术)

现在我们有三个小朋友,由于本题的关系只有2种,于是我们只需召唤一个分身即可
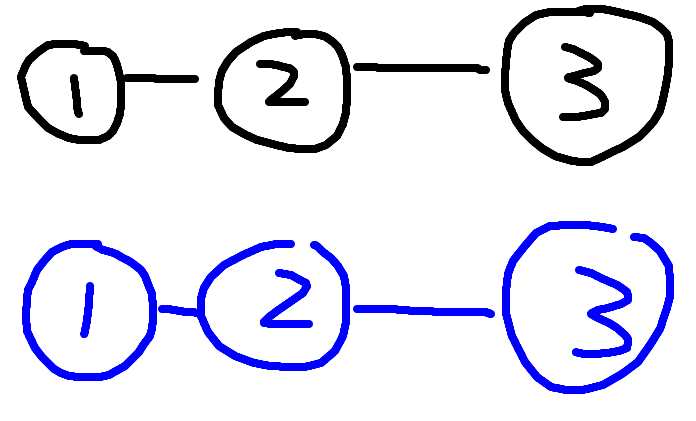
好的我们成功召唤了这三个小朋友的三个分身,我们可以把一个分身a'当做a自己的敌人(上图中连了他们的三条边,但是这并没有什么用。)

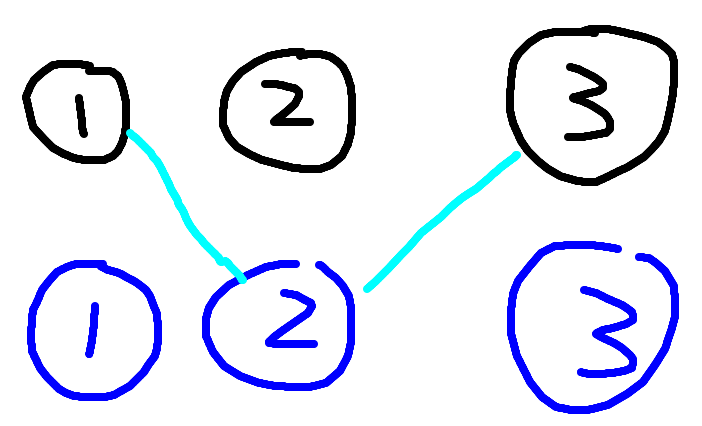
上图中的连边表示这1,2是敌人关系,2,3是敌人关系,这样1,3就借着2的分身成为朋友了。但是这样连边并不完备

这样的连边才是比较完备的。
知道这些就可以写程序了:
1 #include<iostream> 2 #include<cmath> 3 #include<algorithm> 4 #include<queue> 5 using namespace std; 6 const int maxn=300000+10; 7 int read() 8 { 9 int f=1,x=0; 10 char ch=getchar(); 11 if(ch=='-') f=-1; 12 while(ch<'0'||ch>'9') 13 { 14 if(ch=='-')f=-1; 15 ch=getchar(); 16 } 17 while(ch>='0'&& ch<='9') { x=x*10+ch-'0'; ch=getchar(); } 18 return x*f; 19 } 20 int n,m,tp,x,y,f[2*maxn],size[2*maxn];//其中size数组表示一个组所含元素的个数 21 int getf(int n){return f[n]==n ? n : f[n]=getf(f[n]);}//带路径压缩版 22 void merge(int a,int b) 23 { 24 int x=getf(a),y=getf(b); 25 if(x!=y){f[y]=x;size[x]+=size[y];} 26 return; 27 }//合并两个组 28 int main() 29 { 30 n=read();m=read(); 31 for(int i=1;i<=2*n;i++){f[i]=i;}//并查集初始化 32 for(int i=1;i<=n;i++)size[i]=1;//每一个集合初始元素个数都是1 33 while(m--) 34 { 35 tp=read(); 36 if(tp==1) 37 { 38 x=read();y=read(); 39 if(getf(x)==getf(y))printf("Y\n");//这两个人已经是朋友关系了 40 else 41 { 42 merge(x,y+n); 43 merge(y,x+n);//与分身合并 44 printf("N\n"); 45 } 46 } 47 if(tp==2) 48 { 49 x=read(); 50 printf("%d\n",size[getf(x)]-1);//输出x所在集合中元素的个数再-1也就是x朋友的个数(不算自己) 51 } 52 } 53 return 0; 54 }
其中还有一些细节,第一个细节就是分身的存储,分身也应该存在f数组,为了使下标不重复,所以a的分身存在a+n,b的分身存在b+n,以此类推。第二个细节就是并查集合并:在我写的merge函数中,合并的是a所在的集合和b所在的集合,其中合并过程是f[x]=y;(x,y分别是a,b所在集合的标识元素),也就是把b合并到a里,因为题目中会随时询问朋友的个数,但是每一个集合中都包含敌人与朋友,不好处理。所以你可以看到:在第32行代码并查集初始化,每一个集合容量初始为1时,是从1到n,并没有算分身的初始化。因为分身是虚的,所在集合元素个数应该是0.这样的设定带来的好处就是:在合并敌人关系时,更新size数组,敌人不会被算在内。(这个有点难想,需要读者仔细思考,认真体会)。
我们可以再通过食物链这种拥有三种关系的并查集习题来理解一下所谓的“分身术”,下面是代码:
1 #include<iostream> 2 #include<algorithm> 3 #include<cmath> 4 #include<queue> 5 using namespace std; 6 const int maxn=150000+10; 7 int n,k,t[maxn],a[maxn],b[maxn],ans; 8 int f[maxn]; 9 int getf(int x){return x==f[x] ? x : f[x]=getf(f[x]);} 10 void unite(int x,int y) 11 { 12 int a=getf(x),b=getf(y); 13 if(a!=b)f[b]=a; 14 return; 15 } 16 int main() 17 { 18 scanf("%d%d",&n,&k); 19 for(int i=0;i<k;i++) 20 scanf("%d%d%d",&t[i],&a[i],&b[i]); 21 for(int i=0;i<3*n;i++)f[i]=i; 22 for(int i=0;i<k;i++) 23 { 24 int tp=t[i]; 25 int x=a[i]-1,y=b[i]-1; 26 if(x<0 || x>=n || y<0 || y>=n)//输入不合法 27 { 28 ans++; 29 continue; 30 } 31 if(tp==0) 32 { 33 if(getf(x)==getf(y+n) || getf(x)==getf(y+2*n) ) ans++;//属于吃或被吃关系 34 else 35 { 36 unite(x,y); 37 unite(x+n,y+n); 38 unite(x+n*2,y+n*2);//三个分身都合并 39 } 40 } 41 else 42 { 43 if(getf(x)==getf(y) || getf(x)==getf(y+2*n) ) ans++;//同类或被吃关系 44 else 45 { 46 unite(x,y+n); 47 unite(x+n,y+2*n); 48 unite(x+2*n,y);//三个分身交叉合并,表示吃的关系 49 } 50 } 51 } 52 printf("%d",ans); 53 return 0; 54 }
下面以食物链为例,我们介绍第二种方法:带权并查集
食物链一题一共有三种关系:同类,吃,被吃
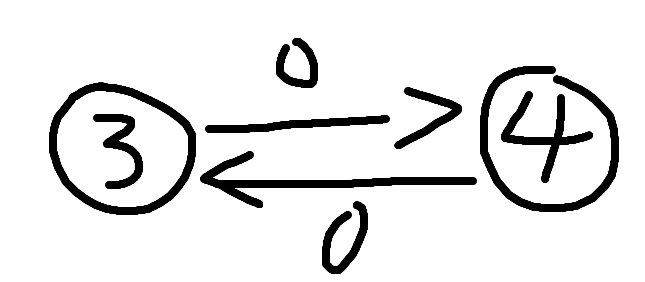
同类权值为0,就像上图

上图中1到2边的权值1,2到1的权值是2,分别表示1吃2,2被1吃
知道这些基础的后,我们就可以通过点点之间的边权的值来弄明白他们之间的关系了,我们用一个r数组来存这种关系,其中r[x]表示从x点指出去边的权值,指向的是f[x]
首先是并查集的基础:查找一个元素所在集合的标识元素

对n做一遍getf函数,顺带路径压缩(过程中顺带更新r[n]):起初n的祖先是f[n],所以节点n到节点f[n]存在一条边权值为r[n],要想求得n到根的边权,需要知道r[f[n]]的值,然后(r[n]+r[f[n]])%3就可算出n到根的关系了(要模3的原因是因为只有三种关系),r[f[n]]的值吗。。就交给伟大的递归了:
1 int getf(int n) 2 { 3 if(f[n]==n)return n; 4 int tmp=f[n];//提前存下f[n]的值,因为程序执行完下一行后f[n]直接就变成n所在集合的表示元素了 5 f[n]=getf(f[n]);//路径压缩 6 r[n]=(r[tmp]+r[n])%3;//公式计算 7 return f[n]; 8 }
会写getf函数后我们再来想想如何写并查集合并的程序,在此题中针对两个动物a,b我们是先知道他们之间的关系,才进行合并的,所以

图中x,y分别是a,b所在集合的标识元素,在merge过程中,我们遵循y连到x的规则(其实都一样),因为在未合并前,集合x和集合y是两个没有任何关系的集合,多了a到b的关系后,才建立联系的。这里有一个非常非常重要的结论:一个并查集中从一个点出发,沿着它所指向的边一直走,并累加下路上的权值(如果边是反的那么就取权值的负数),走一圈回来,累加的和模3结果一定是0.这个我也不怎么会证明,但是读者可以通过类似矢量的东西来理解这个结论,应该不算太难吧。根据这个结论和上图,我们能得到一个等式:(r[b]+r[y]+k-r[a])%3=0,其中k是a到b的关系,这个边其实在并查集中是不存在的,但是加上这条边能更好的解释。在这个等式里面,有哪些是我们不知道的呢?只有r[y],所以在合并时我们只需算出r[y]的值即可。r[y]=(r[a]-k-r[b]+3)%3,这个是由刚才的等式推出的,其中有一个+3是为了防负数的。
知道这些其实就可以做题了,本题的意思是找出所有不合法信息的个数,不合法信息包括数字问题,还有的就是并查集之间的冲突。对于输入的两个数a,b,如果是两个未知关系的元素,我们就进行正常的并查集合并就可以了,如果他们之前有关系(即在一个集合之中)我们就需要分析他们的关系是否正确了。

由于r[a],r[b]存储的都是a,b与他们的标识元素之间的关系,无法直接得出a和b的关系,但是假设a,b之间存在一个关系k,如果等式(k+r[b]-r[a]+3)%3=0的话,那么关系就就是正确的了,反之,则不对。
下面贴代码:
1 #include<iostream> 2 #include<algorithm> 3 #include<cmath> 4 #include<cstring> 5 using namespace std; 6 int f[50010],r[50010],cnt,n,k,tp,a,b,x,y; 7 int getf(int n) 8 { 9 if(f[n]==n)return n; 10 int tmp=f[n]; 11 f[n]=getf(f[n]); 12 r[n]=(r[tmp]+r[n])%3; 13 return f[n]; 14 } 15 int main() 16 { 17 scanf("%d%d",&n,&k); 18 for(int i=1;i<=n;i++)f[i]=i; 19 while(k--) 20 { 21 scanf("%d%d%d",&tp,&a,&b); 22 if(a<1 || a>n || b<1 || b>n){cnt++;continue;}//数字非法 23 x=getf(a);y=getf(b);//找根 24 if(x!=y) 25 { 26 f[x]=y;//这里的合并与上面不同,是把x合并到y; 27 r[x]=(r[b]-r[a]+tp+999)%3;//我这里写了999,并没有写3,其实都一样 28 } 29 else if((tp+r[b]-r[a])%3) cnt++;//判断关系是否正确 30 } 31 printf("%d",cnt); 32 return 0; 33 }
然后我们再来看看敌人这道题,用带权并查集做
1 #include<iostream> 2 #include<algorithm> 3 #include<cmath> 4 #include<cstring> 5 using namespace std; 6 const int maxn=300000+10; 7 int f[maxn],r[maxn],size1[maxn],size2[maxn],n,k,tp,a,b,x,y; 8 int read() 9 { 10 int f=1,x=0; 11 char ch=getchar(); 12 if(ch=='-') f=-1; 13 while(ch<'0'||ch>'9') 14 { 15 if(ch=='-')f=-1; 16 ch=getchar(); 17 } 18 while(ch>='0'&& ch<='9') { x=x*10+ch-'0'; ch=getchar(); } 19 return x*f; 20 } 21 int getf(int n) 22 { 23 if(f[n]==n)return n; 24 int tmp=f[n]; 25 f[n]=getf(f[n]); 26 r[n]=(r[tmp]+r[n])%2; 27 return f[n]; 28 } 29 int main() 30 { 31 n=read();k=read(); 32 for(int i=1;i<=n;i++) 33 { 34 f[i]=i; 35 size1[i]=1; 36 } 37 while(k--) 38 { 39 tp=read(); 40 if(tp==1) 41 { 42 a=read();b=read(); 43 x=getf(a),y=getf(b); 44 if(x==y) 45 { 46 if((r[a]-r[b]+2)%2==0) printf("Y\n");//是朋友关系 47 else printf("N\n"); 48 } 49 else 50 { 51 printf("N\n"); 52 f[x]=y; 53 r[x]=(r[b]-r[a]+132245)%2;//这里的132245也是我闲的,只要是一个大于等于3的奇数即可(1+2,其中1为a与b的关系,2为防止负数) 54 if(r[x]==0) 55 { 56 size1[y]+=size1[x]; 57 size2[y]+=size2[x]; 58 } 59 else 60 { 61 size1[y]+=size2[x]; 62 size2[y]+=size1[x]; 63 } 64 } 65 } 66 else 67 { 68 a=read(); 69 x=getf(a); 70 if(r[a]==1) printf("%d\n",size2[x]-1); 71 else printf("%d\n",size1[x]-1); 72 } 73 } 74 return 0; 75 }
这道题多了一个随时询问并查集中朋友的个数,我们用两个数组来维护,一个是size1,一个是size2,size1[x]表示在以X为标识元素的集合中x朋友的个数,size2相反,便是x的敌人了。在合并时X到y时,需要判断一下,如果r[x]=0即X与y是朋友关系,那x的朋友也是y的朋友,x的敌人也是y的敌人。合并执行size1[y]+=size1[x];size2[y]+=size2[x];即可,反之如果r[x]=1即X与y是敌人关系,那x的朋友是y的敌人,x的敌人是y的朋友。合并执行size1[y]+=size2[x];size2[y]+=size1[x];在
在最后输出时,也要判断一下,根据所求元素a与a的标识元素x的关系来确定,究竟是输出size1还是size2(勿忘减一,不算自己)
最后再提一句,食物链还有高级版本:就是不止有三种动物了,有n种,在这个题目下精神分裂法就显得不是那么厉害了,需要两两合并,十分麻烦,用带权并查集就快多了,只需在原题中改几个数就可以了,幸亏在n<=10.哈哈哈哈


 浙公网安备 33010602011771号
浙公网安备 33010602011771号