AcWing 796. 子矩阵的和

二维前缀和

定义

我们用 \(sum\) 数组表示原矩阵的二维前缀和，\(sum_{i, j}\) 表示左上角 \((1, 1)\) 、右下角 \((i, j)\) 的子矩阵的和。

作用

求任意子矩阵的和。

具体如何求？

求二维前缀和

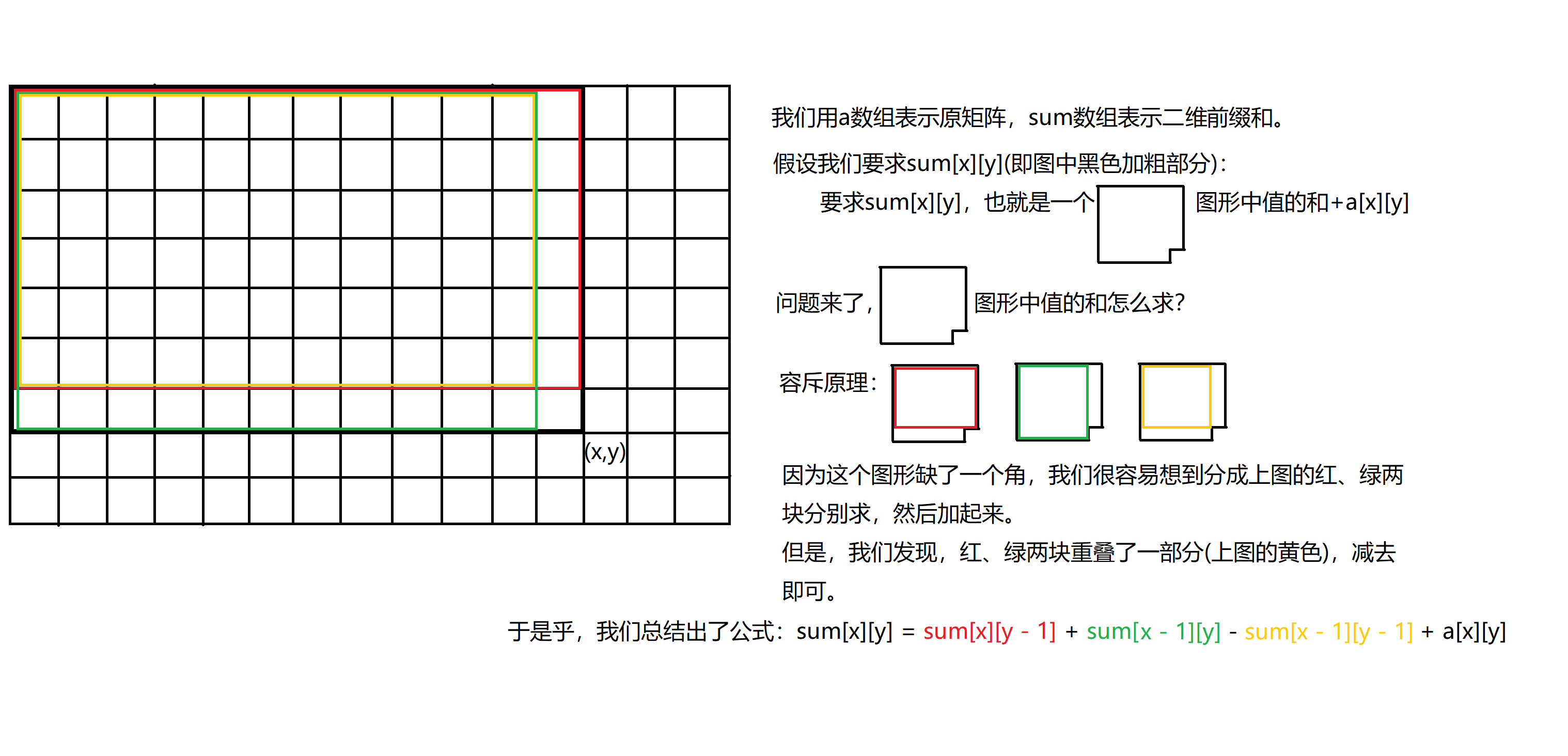
求任意子矩阵和

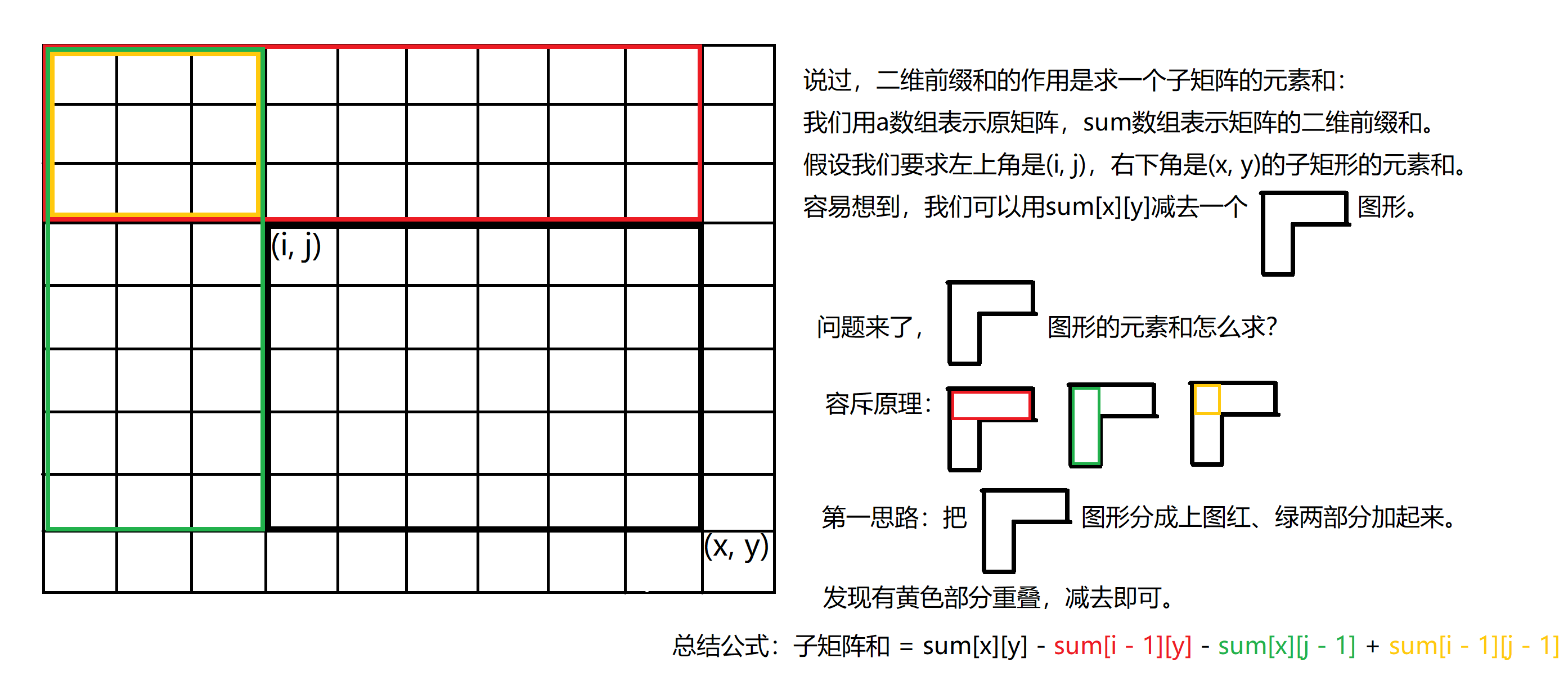
代码（公式都体现了）

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;

const int N = 1010;

int n, m, q;
int a[N][N], sum[N][N];
int x, y, xx, yy;

int main()
{
    cin >> n >> m >> q;
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
        {
            cin >> a[i][j];
            sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + a[i][j]; //求二维前缀和
        }
    while (q -- )
    {
        cin >> x >> y >> xx >> yy;
        cout << sum[xx][yy] - sum[x - 1][yy] - sum[xx][y - 1] + sum[x - 1][y - 1] << endl; //求任意子矩阵和
    }
    return 0;
}