AcWing 789. 数的范围

一道整数二分模板题。

二分介绍

二分查找是一种算法，其输入是一个元素列表，注意：列表必须是有 二段性 的（二分的本质不是单调性，而是二段性）。

二分查找通常用于：

• 序列中是否存在满足某条件的元素；
• 序列中第一个满足某条件的元素的位置；
• 序列中最后一个满足某条件的元素的位置。

二分思想

确定查找区间 \([l, r]\)，取区间中间值 \(mid = (l + r) \div 2\)，判断 \(mid\) 是否满足题目要求，舍弃无效区间(\(mid = l\) 或 \(mid = r\))。

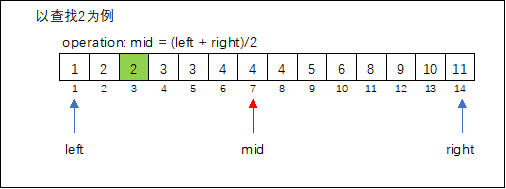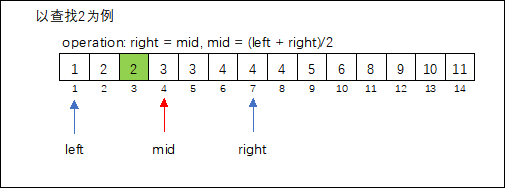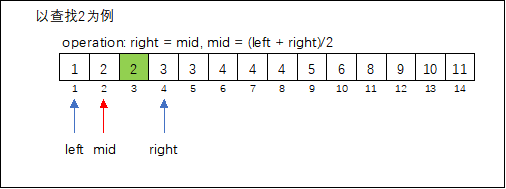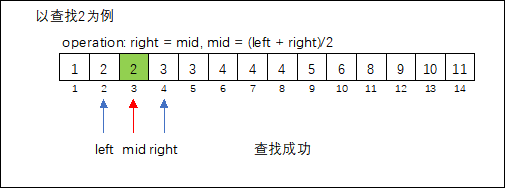
算法模板

共有两个，适用于不同情况。

bool check(int x) // 检查x是否满足某种性质
{
    /*……*/
}

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid; // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}

// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1; //防止死循环，这里要+1
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

代码实现

套用模板即可。

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;

const int N = 100010;

int a[N]; //保证有序

int main()
{
    int n, q, k;
    scanf("%d%d", &n, &q);
    for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
    //对于每个询问
    for (int i = 0; i < q; i ++ )
    {
        scanf("%d", &k);
        int l = 0, r = n - 1;
        while (l < r) //找左边界
        {
            int mid = l + r >> 1;
            if (a[mid] >= k) r = mid;
            else l = mid + 1;
        }
        if (a[l] == k) //存在
        {
            printf("%d ", l);
            l = 0, r = n - 1;
            while (l < r) //找右边界
            {
                int mid = l + r + 1 >> 1;
                if (a[mid] <= k) l = mid;
                else r = mid - 1;
            }
            printf("%d\n", l);
        }
        else printf("-1 -1\n"); //不存在
    }
    return 0;
}

为什么找左边界是 \(a_{mid}≥k\),而找右边界是 \(a_{mid}≤k\) 呢？

• 为了找最左边界，需要判断条件是大于等于，这样，中位值大于等于目标值，才会继续向左找左边界。
• 为了找最右边界，需要判断条件是小于等于，这样，中位值小于等于目标值，才会继续向右找右边界。