图像处理人脸识别的三种经典算法与简单的CNN 【附Python实现】

一点说明

1. 完成情况

详细阐述了人脸识别中的经典算法与深度学习算法
手动实现了三种人脸识别经典算法【代码地址】
- 基于主成分分析（PCA）的Eigenfaces特征脸方法
- 基于线性判别分析（LDA）的Fisherfaces特征脸方法
- 局部二进制模式（LBP）直方图方法
实验对比分析了三种人脸识别经典算法和 CNN 实现人脸识别的特点以及异同点

2. 项目结构

data/（存放项目用到的数据集，如有更改，记得修改代码中的引用地址）
src/（存放源代码，直接运行 src/ 中的 Classical_Methods.py 即可）
README.md （实验报告）

思路分析

0. 人脸识别综述

参考链接：《Face Recognition: From Traditional to Deep Learning Methods》，《人脸识别合集 | 人脸识别概述》

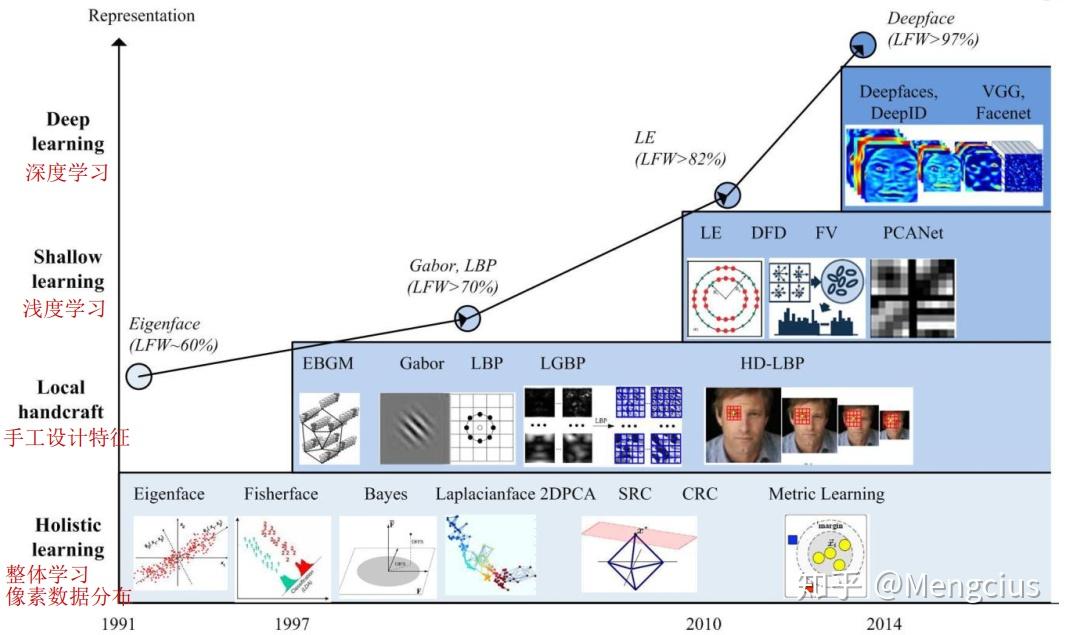
人脸识别（Face Recognition）是指能够识别或验证图像或视频中的主体的身份的技术。自上个世纪七十年代首个人脸识别算法被提出以来，人脸识别已经成为了计算机视觉与生物识别领域被研究最多的主题之一。究其火爆的原因，一方面是它的挑战性——在无约束条件的环境中的人脸信息，也就是所谓自然人脸（Faces in-the-wild），具有高度的可变性，如下图所示；另一方面是由于相比于指纹或虹膜识别等传统上被认为更加稳健的生物识别方法，人脸识别本质上是非侵入性的，这意味着它是最自然、最符合人类直觉的一种生物识别方法。

现代人脸识别技术的研究热潮，已经从使用人工设计的特征（如边和纹理描述量等）与机器学习技术（如主成分分析、线性判别分析和支持向量机等）组合的传统方法的研究，逐渐转移到使用庞大人脸数据集搭建与在其基础上训练深度神经网络的研究。但是，无论是基于传统方法还是深度神经网络，人脸识别的流程都是相似的，大概由以下四个模块组成：

人脸检测 ：提取图像中的人脸，划定边界；
人脸对齐 ：使用一组位于图像中固定位置的参考点来缩放和裁剪人脸图像；
人脸表征 ：人脸图像的像素值会被转换成紧凑且可判别的特征向量，或称模板；
人脸匹配 ：选取并计算两个模板间的相似度分数来度量两者属于同一个主体的可能性。

preview

1. 传统算法——主成分分析（PCA）与线性判别分析（LDA）

准确地说，是 基于主成分分析的Eigenfaces特征脸方法 与 基于线性判别分析的Fisherfaces特征脸方法，这是根据整体特征进行人脸辨别的两种方法。

1）算法框架

使用 PCA 或 LDA 进行人脸识别的算法流程十分相似，具体步骤如下。

读取人脸图片数据库的图像及标签，并进行灰度化处理（可以同时进行直方图均衡等）
将读入的二维图像数据信息转为一维向量，然后按列组合成原始数据矩阵
对原始矩阵进行归一化处理，并使用PCA或LDA算法对原始数据矩阵进行特征分析与降维（计算过程中，根据原始数据得到一维均值向量经过维度的还原以后得到的图像为“平均脸”）
读取待识别的图像，将其转化为与训练集中的同样的向量表示，遍历训练集，寻找与待识别图像的差值小于阈值（或差值最小）的图像，即为识别结果

2）PCA 原理

参考链接：《PCA的数学原理》（强烈推荐，讲得非常透彻！）

PCA（Principal Component Analysis，主成分分析）是一种常用的数据分析方法。PCA通过线性变换将原始数据变换为一组各维度线性无关的表示，可用于提取数据的主要特征分量，常用于高维数据的降维。

I. 为什么要降维？

数据分析时，原始数据的维度与算法的复杂度有着密切的关系，在保留原始数据特征的情况下，对数据进行降维可以有效地提高时间效率，减少算力损失。

II. PCA降维的原理是什么？

降维意味着信息的丢失，但是由于实际数据内部往往具有相关性，所以我们可以利用这种相关性，通过某些方法使得在数据维度减少的同时保留尽可能多的原始特征，这就是PCA算法的初衷。

那么这一想法如何转化为算法呢？我们知道，在N维空间对应了由N个线性无关的基向量构成的一组基，空间中的任一向量都可用这组基来表示。我们要将一组N维向量降为K维（K大于0，小于N），其实只需要通过矩阵乘法将原N维空间中的向量转化为由K个线性无关的基向量构成的一组基下的表示。

但是，这一组K维的基并不是随便指定的。为了尽可能保留原始特征，我们希望将原始数据向量投影到低维空间时，投影后各字段（行向量）不重合（显然重合会覆盖特征），也就是使变换后数据点尽可能分散，这就自然地联系到了线性代数中的方差与协方差。

所以，综合来看，我们降维的目标为选择K个基向量（一般转化为单位长度的正交基），使得原始数据变换到这组基上后，各字段两两间协方差为0，而字段的方差则尽可能大（在正交的约束下，取最大的K个方差）。这也就是PCA的原理——PCA本质上是将方差最大的方向作为主要特征，并且在各个正交方向上将数据“离相关”，也就是让它们在不同正交方向上没有相关性。

III. 如何使用PCA进行降维？

在上一个问题中，我们其实已经介绍了PCA的算法流程。转化成具体的数学方法，主要有以下几步（设有 $m$ 条 $n$ 维数据，将其降为 $k$ 维）：

将原始数据按列组成 $n$ 行 $m$ 列矩阵 $X$
矩阵 $X$ 中每一维的数据都减去该维的均值，使得变换后矩阵 $X’$ 每一维均值为 $0$
求出协方差矩阵 $C=\frac{1}{m}X'X'^T$，进一步求出矩阵 $C$ 的特征值及对应的特征向量
将特征向量按对应特征值大小从上到下按行排列成矩阵，取前 $k$ 行组成矩阵 $P$
$Y=PX$ 即为降维到 $k$ 维后的数据

IV. PCA的缺点与不足

PCA是一种无参数技术，无法进行个性化的优化；PCA可以解除线性相关，但无法处理高阶的相关性；PCA假设数据各主特征分布在正交方向，无法较好应对主特征在非正交方向的情况。

V. PCA 的 python 实现

用 Python 语言实现上述算法，代码如下，仅展示代码核心部分，详细代码请见附件。

参考链接：《人脸识别经典算法实现（一）——特征脸法》，《opencv学习之路（40）、人脸识别算法——EigenFace、FisherFace、LBPH》，《经典人脸识别算法小结——EigenFace, FisherFace & LBPH（下）》

def algorithm_pca(data_mat):
    """
    PCA函数，用于数据降维
    :param data_mat: 样本矩阵
    :return: 降维后的样本矩阵和变换矩阵
    """
    mean_mat = np.mat(np.mean(data_mat, 1)).T
    cv2.imwrite('./data/face_test/mean_face.jpg', np.reshape(mean_mat, IMG_SIZE))

    diff_mat = data_mat - mean_mat
    # print('差值矩阵', diff_mat.shape, diff_mat)
    cov_mat = (diff_mat.T * diff_mat) / float(diff_mat.shape[1])
    # print('协方差矩阵', cov_mat.shape, cov_mat)

    eig_vals, eig_vecs = np.linalg.eig(np.mat(cov_mat))
    # print('特征值（所有）：', eig_vals, '特征向量（所有）：', eig_vecs.shape, eig_vecs)

    eig_vecs = diff_mat * eig_vecs
    eig_vecs = eig_vecs / np.linalg.norm(eig_vecs, axis=0)
    eig_val = (np.argsort(eig_vals)[::-1])[:DIM]
    eig_vec = eig_vecs[:, eig_val]
    # print('特征值（选取）：', eig_val, '特征向量（选取）：', eig_vec.shape, eig_vec)

    low_mat = eig_vec.T * diff_mat
    # print('低维矩阵：', low_mat)

    return low_mat, eig_vec

3）LDA 原理

参考链接：《Linear Discriminant Analysis》，《人脸识别经典算法三：Fisherface（LDA）》，《人脸识别系列二 | FisherFace，LBPH算法及Dlib人脸检测》

LDA（Linear Discriminant Analysis，线性判别分析）算法的思路与PCA类似，都是对图像的整体分析。不同之处在于，PCA是通过确定一组正交基对数据进行降维，而LDA是通过确定一组投影向量使得数据集不同类的数据投影的差别较大、同一类的数据经过投影更加聚合。在形式上，PCA与LDA的最大区别在于，PCA中最终求得的特征向量是正交的，而LDA中的特征向量不一定正交。

I. LDA的原理是什么？

在上面我们已经介绍了LDA的目标：不同的分类得到的投影点要尽量分开；同一个分类投影后得到的点要尽量聚合。

为了定量分析这两点，以计算合适的投影矩阵，我们定义了类内散列度矩阵 $S_{w}$和类间散列度矩阵 $S_B $ 。其中 $S_w=\sum ^c_{i=1}{\sum _{x\in ω_i}(x-μ_i)(x-μ_i)^T}$, $c$ 为类别总数，$μ_i$代表类别 $i$ 的均值矩阵；$S_B=\sum ^c_{i=1}N_i(μ_i-μ)(μ_i-μ)^T$，$N_i$ 为类别$i$ 的数据点数。定义 $J(w)=\frac{|W^TS_BW|}{|W^TS_wW|}$ 为目标函数，其中矩阵 $W$ 是投影矩阵，那么我们就是要求出使 $J(w)$ 取最大值的投影矩阵 $W$ 。该最大值可由拉格朗日乘数法求得，不再赘述。最终问题可化简为，$S_w^{-1}S_Bw_i=λw_i$ ，即求得矩阵的特征向量，然后取按特征值从大到小排列的前 $k$ 个特征向量即为所需的投影矩阵。

II. LDA 与 PCA 的比较

LDA与PCA算法的不同之处：
- 从数学角度来看，LDA选择分类性能最好的投影方向，而PCA选择样本投影点具有最大方差的方向；
- LDA是有监督的降维方法，而PCA是无监督的；
- 对于 $K$ 维的数据，LDA只能将其降到 $K-1$ 维度，而 PCA 不受此限制。
LDA与PCA算法的相同之处：
- 在降维的时候，两者都使用了矩阵的特征分解思想；
- 两种算法都假设数据集中原始数据符合高斯分布。

III. LDA 的 python 实现

用python语言实现上述算法，代码如下，仅展示代码核心部分，详细代码请见附件。

参考链接：《人脸识别经典算法实现（二）——Fisher线性判别分析》，《opencv学习之路（40）、人脸识别算法——EigenFace、FisherFace、LBPH》，《经典人脸识别算法小结——EigenFace, FisherFace & LBPH（下）》

def algorithm_lda(data_list):
    """
    多分类问题的线性判别分析算法
    :param data_list: 样本矩阵列表
    :return: 变换后的矩阵列表和变换矩阵
    """
    n = data_list[0].shape[0]
    Sw = np.zeros((n, n))
    u = np.zeros((n, 1))
    Sb = np.zeros((n, n))
    N = 0
    mean_list = []
    sample_num = []

    for data_mat in data_list:
        mean_mat = np.mat(np.mean(data_mat, 1)).T
        mean_list.append(mean_mat)
        sample_num.append(data_mat.shape[1])
        data_mat = data_mat - mean_mat
        Sw += data_mat * data_mat.T

    for index, mean_mat in enumerate(mean_list):
        m = sample_num[index]
        u += m * mean_mat
        N += m
    u = u / N

    for index, mean_mat in enumerate(mean_list):
        m = sample_num[index]
        sb = m * (mean_mat - u) * (mean_mat - u).T
        Sb += sb

    eig_vals, eig_vecs = np.linalg.eig(np.mat(np.linalg.inv(Sw) * Sb))
    eig_vecs = eig_vecs / np.linalg.norm(eig_vecs, axis=0)
    eig_val = (np.argsort(eig_vals)[::-1])[:DIM]
    eig_vec = eig_vecs[:, eig_val]

    trans_mat_list = []
    for data_mat in data_list:
        trans_mat_list.append(eig_vec.T * data_mat)
    return trans_mat_list, eig_vec

3. 传统算法——局部二进制模式直方图（LBPH）

LBPH算法“人”如其名，采用的识别方法是局部特征提取的方法，这是与前两种方法的最大区别。类似的局部特征提取算法还有离散傅里叶变换（DCT）与盖伯小波（Gabor Waelets）等。

LBPH（Local Binary Pattern Histograms，局部二进制模式直方图）人脸识别方法的核心是 LBP算子。LBP是一种用来描述图像局部纹理特征的算子，它反映内容是每个像素与周围像素的关系。

I. LBP 的原理是什么？

参考链接：《LBP简介》，《人脸识别经典算法二：LBP方法》

原始 LBP

最初的LBP是定义在像素3x3邻域内的，以邻域中心像素为阈值，将相邻的8个像素的灰度值与其进行比较，若周围像素值大于中心像素值，则该像素点的位置被标记为1，否则为0。这样，3x3邻域内的8个点经比较可产生8位二进制数（通常转换为十进制数即LBP码，共256种），即得到该邻域中心像素点的LBP值，并用这个值来反映该区域的纹理信息。如下图所示：
均匀 LBP（本次作业中代码采用的LBP算子）

研究者发现根据原始LBP计算出来的90%以上的值具有某种特性，即属于均匀模式（Uniform Pattern）——二进制序列（这个二进制序列首尾相连）中数字从0到1或是从1到0的变化不超过2次。比如，01011111的变化次数为3次，那么该序列不属于均匀模式。根据这个算法，所有的8位二进制数中共有58（变化次数为0的有2种，变化次数为1的有0种，变化次数为2的有56种）个均匀模式。

所以，我们可以根据这一数据分布特点将原始的LBP值分为59类，58个均匀模式为一类，其余为第59类。这样就将直方图从原来的256维变成了59维，起到了降维的效果。

III. LBPH 的算法流程

LBPH的算法其实非常简单，只有两步：

LBP特征提取：根据上述的均匀LBP算子处理原始图像；
LBP特征匹配（计算直方图）：将图像分为若干个的子区域，并在子区域内根据LBP值统计其直方图，以直方图作为其判别特征。

III. LBP 的特点？

LBP的优点是对光照不敏感。根据算法，每个像素都会根据邻域信息得到一个LBP值，如果以图像的形式显示出来可以得到下图。相比于PCA或者LDA直接使用灰度值去参与运算，LBP算子是一种相对性质的数量关系，这是LBP应对不同光照条件下人脸识别场景的优势所在。但是对于不同角度、遮挡等场景，LBP也无能为力。

IV. LBPH 的 python 实现

用python语言实现上述算法，代码如下，仅展示代码核心部分，详细代码请见附件。

参考链接：《人脸识别经典算法实现（三）——LBP算法》，《opencv学习之路（40）、人脸识别算法——EigenFace、FisherFace、LBPH》，《经典人脸识别算法小结——EigenFace, FisherFace & LBPH（下）》

class AlgorithmLbp(object):
    def load_img_list(self, dir_name):
        """
        加载图像矩阵列表
        :param dir_name:文件夹路径
        :return: 包含最原始的图像矩阵的列表和标签矩阵
        """
        # 请见附件

    def get_hop_counter(self, num):
        """
        计算二进制序列是否只变化两次
        :param num: 数字
        :return: 01变化次数
        """
        bin_num = bin(num)
        bin_str = str(bin_num)[2:]
        n = len(bin_str)
        if n < 8:
            bin_str = "0" * (8 - n) + bin_str
        n = len(bin_str)
        counter = 0
        for i in range(n):
            if i != n - 1:
                if bin_str[i + 1] != bin_str[i]:
                    counter += 1
            else:
                if bin_str[0] != bin_str[i]:
                    counter += 1
        return counter

    def get_table(self):
        """
        生成均匀对应字典
        :return: 均匀LBP特征对应字典
        """
        counter = 1
        for i in range(256):
            if self.get_hop_counter(i) <= 2:
                self.table[i] = counter
                counter += 1
            else:
                self.table[i] = 0
        return self.table

    def get_lbp_feature(self, img_mat):
        """
        计算LBP特征
        :param img_mat:图像矩阵
        :return: LBP特征图
        """
        m = img_mat.shape[0]
        n = img_mat.shape[1]
        neighbor = [0] * 8
        feature_map = np.mat(np.zeros((m, n)))
        for y in range(1, m - 1):
            for x in range(1, n - 1):
                neighbor[0] = img_mat[y - 1, x - 1]
                neighbor[1] = img_mat[y - 1, x]
                neighbor[2] = img_mat[y - 1, x + 1]
                neighbor[3] = img_mat[y, x + 1]
                neighbor[4] = img_mat[y + 1, x + 1]
                neighbor[5] = img_mat[y + 1, x]
                neighbor[6] = img_mat[y + 1, x - 1]
                neighbor[7] = img_mat[y, x - 1]
                center = img_mat[y, x]
                temp = 0
                for k in range(8):
                    temp += (neighbor[k] >= center) * (1 << k)
                feature_map[y, x] = self.table[temp]
        feature_map = feature_map.astype('uint8') 
        return feature_map

    def get_hist(self, roi):
        """
        计算直方图
        :param roi:图像区域
        :return: 直方图矩阵
        """
        hist = cv2.calcHist([roi], [0], None, [59], [0, 256]) 
        return hist

4. 神经网络——卷积神经网络（CNN）

CNN（Convolutional Neural Networks，卷积神经网络）是人脸识别方面最常用的一类深度学习方法。深度学习方法的主要优势是可用大量数据来训练，从而学到对训练数据中出现的变化情况稳健的人脸表征。这种方法不需要设计对不同类型的类内差异（比如光照、姿势、面部表情、年龄等）稳健的特定特征，而是可以从训练数据中学到它们。

深度学习方法的主要短板是它们需要使用非常大的数据集来训练，而且这些数据集中需要包含足够的变化，从而可以泛化到未曾见过的样本上。幸运的是，一些包含自然人脸图像的大规模人脸数据集已被公开；不幸的是，本人设备算力实在有限，无法支持在大数据集上运行深度学习代码。

I. 深度学习的几个经典的案例

参考链接：《人脸识别合集 | 绪论与目录》，《Face Recognition: From Traditional to Deep Learning Methods》

DeepFace，2014年

DeepFace主要先训练Softmax多分类器人脸识别框架；然后抽取特征层，用特征再训练另一个神经网络、孪生网络或组合贝叶斯等人脸验证框架。想同时拥有人脸验证和人脸识别系统，需要分开训练两个神经网络。但线性变换矩阵W的大小随着身份数量n的增加而线性增大。

DeepFace的主要贡献是，（1）一个基于明确的 3D 人脸建模的高效的人脸对齐系统；（2）一个包含局部连接的层的 CNN 架构，这些层不同于常规的卷积层，可以从图像中的每个区域学到不同的特征。
DeepID系列，2014年

DeepID框架与DeepFace类似，采用的是 CNN+Softmax；而DeepID2、DeepID2+、DeepID3都采用 CNN+Softmax+Contrastive Loss，使得同类特征的L2距离尽可能小，不同类特征的L2距离大于某个间隔。
FaceNet，2015年

2015年FaceNet提出了一个绝大部分人脸问题的统一解决框架，直接学习嵌入特征，然后人脸识别、人脸验证和人脸聚类等都基于这个特征来做。FaceNet在 DeepID2 的基础上，抛弃了分类层，再将 Contrastive Loss 改进为 Triplet Loss，获得类内紧凑和类间差异。但人脸三元组的数量出现爆炸式增长，特别是对于大型数据集，导致迭代次数显著增加；样本挖掘策略造成很难有效的进行模型的训练。

II. 深度学习的算法流程

参考链接：《人脸识别合集 | 人脸识别概述》，《Face Recognition: From Traditional to Deep Learning Methods》

用于人脸识别的 CNN 模型主要有以下两种设计思路：

基于度量的学习：通过优化配对的人脸或人脸三元组之间的距离度量来直接学习人脸表征（常称为瓶颈特征，bottleneck features）；
基于分类的学习：训练集中的每个主体都对应一个类别，通过去除分类层并将之前层的特征用作瓶颈特征而将该模型用于识别不存在于训练集中的主体。在这第一个训练阶段之后，该模型可以使用其它技术来进一步训练，从而为目标应用优化瓶颈特征（比如使用联合贝叶斯或使用一个不同的损失函数来微调该 CNN 模型）。

III. Python实现

卷积神经网络部分的代码非本人编写，希望老师与助教知悉。【引用地址】

与电脑环境斗争一天的我，面对无数的DDL，遂选择搁置，日后我会将重新编写的代码放在我的博客中。但为了使报告更加完整，兼顾传统方法与深度学习方法，综合对比不同方法在人脸识别中的表现，我使用了 17373489 张佳一 同学的 CNN 代码与数据（见结果分析部分）。

#实现CNN卷积神经网络，并测试最终训练样本实现的检测概率
#tf.layer方法可以直接实现一个卷积神经网络的搭建
#通过卷积方法实现
layer1 = tf.layers.conv2d(inputs=data_input, filters = 32,kernel_size=2,
strides=1,padding='SAME',activation=tf.nn.relu)
#实现池化层，减少数据量，pool_size=2表示数据量减少一半
layer1_pool = tf.layers.max_pooling2d(layer1,pool_size=2,strides=2)
#第二层设置输出，完成维度的转换，以第一次输出作为输入，建立n行的32*32*32输出
layer2 = tf.reshape(layer1_pool,[-1,32*32*32])
#设置输出激励函数
layer2_relu = tf.layers.dense(layer2, 1024, tf.nn.relu)
#完成输出，设置输入数据和输出维度
output = tf.layers.dense(layer2_relu, num_people)
#建立损失函数
loss =
tf.losses.softmax_cross_entropy(onehot_labels=label_input,logits=output)
#使用梯度下降法进行训练
train = tf.train.GradientDescentOptimizer(0.01).minimize(loss)
#定义检测概率
accuracy = tf.metrics.accuracy(
labels=tf.arg_max(label_input, 1), predictions=tf.arg_max(output, 1))
[1]

结果分析

0. 数据集说明

I. 基本信息（数据集地址）

数据集中共包含395人（男性和女性）的人脸图像，每人20张图像；
数据集中人来自不同种族（但鲜有东方人）；
主要是大学一年级的本科生，故大多数的个体在18-20岁之间，但也有一些年龄较大的个体；
数据集划分为四个子集，分别为Faces94、Faces95、Faces96以及Grimace，识别难度递增。

II. 数据集展示

Faces94（153人）	Faces95（72人）	Faces96（152人）	Grimace（18人）

1. 主成分分析（PCA）

I. PCA算法中的 “平均脸” 与 “特征脸”

在代码实现部分，我将 均值矩阵 与 特征矩阵 重新映射到 $[0,255]$ 的灰度值区间，得到了所谓 “平均脸” 与 “特征脸”。（从上到下，依次为在 Faces94、Faces95、Faces96、Grimace的结果）


平均脸	特征脸 1	特征脸 2	特朗普 3 😜	特征脸 4


平均脸	特征脸 1	特征脸 2	特征脸 3	特征脸 4


平均脸	特征脸 1	特征脸 2	特征脸 3	特征脸 4


平均脸	特征脸 1	特征脸 2	特征脸 3	特征脸 4

II. 准确率与消耗时间

这里展示的是该算法在不同数据集上识别的准确率，以及在本机上运行的时间（单位：ms）。

Faces94	Faces95

Faces96	Grimace

III. PCA 结果分析

准确率方面：我们发现，PCA在Faces94与Grimace上的识别准确率竟然达到了100%，Faces96上次之，而在Faces95上的识别率最低。这与我们的预期大相径庭。结合“平均脸”与数据集特征，——Faces95数据集中人脸的角度变化较大，而Faces96中背景的干扰较大——我认为应该是因为在代码实现时，数据预处理中没有进行良好的人脸检测与对齐，这也反映了，PCA在适应背景干扰与人脸角度变化方面，表现不佳；
识别速度方面：随数据集规模扩大，识别耗时基本呈指数增长的趋势（橙色虚线为指数拟合曲线）。

2. 线性判别分析（LDA）

代码运行在Faces94与Faces95子集上会出现数组溢出的BUG，这与数据集中非法数据（类别中不足20张，包含.gif图片等）有关，需要对数据集进行过滤，现仅在其余两个数据集上测试。

I. LDA中的平均脸

Faces96	Grimace

II. 准确率与消耗时间

Faces96	Grimace

III. LDA 结果分析

准确率方面：实验结果显示，LDA在Faces96上表现不佳，而在Grimace上则达到了100%识别。分析其原因，LDA；
识别速度方面：与PCA技术相比，一般情况下，在相同的数据集上，LDA算法耗时要比PCA长，且当数据集增大时，LDA算法耗时与PCA的差值逐渐增大；但是，当数据集较小时，LDA的速度反而比PCA略快。

3. 局部二进制模式直方图（LBPH）

I. LBPH 中间图像

注意，为了提高识别效率，在图片读取时，我已经将原图尺寸统一调整为 50 × 50 。

原图	原始LBP	均衡模式

II. 准确率与消耗时间

LBPH人脸比对时间过长，在测试时，我将其读取到的图片调整为20 × 20，以提高识别速度。

Faces94	Faces95

Faces96	Grimace

III. 结果分析

识别准确率上来看，LBPH总体表现较好，在大部分情况下都表现较好，尤其是在Faces94和Grimace上取得较好的识别效果，但是在Faces95数据集上的识别效果不佳。这应该与我在图片压缩时，将图片从 180 × 200 压缩到 20 × 20 所造成的局部信息损失有关。
识别速度上来看，LBPH的人脸表征的提取阶段耗时较短，但是人脸识别阶段耗时较长，这是因为每次识别都要遍历训练集中所有图片进行计算（可以通过调整图片压缩比以及直方图划块的大小来调整识别的时间复杂度）。

IV. 三种经典算法的准确率对比

不同算法下，在不同特点的数据集中，人脸识别准确率的对比如下。

V. 三种经典算法的速度对比

运行算法进行人脸表征提取所需时间（单位：ms）。

不同算法进行人脸识别所需时间（单位：ms）。

4. 卷积神经网络（CNN，分类模型）

用到的数据集：PIE dataset ，包含了68个人在五种不同姿态下的共11554张面部图像数据，并以MAT格式的文件保存。

I. 准确率与损失函数收敛情况

Pose07	Pose09	Pose27	Pose29

II. 分析（与经典算法的对比）

我们发现，当训练的数据集规模不足够大时，反而传统方法的效果可能更好一些，因为传统方法是人们基于图像的某些规律，通过数学分析推导出的能够较好地描述图像中人脸特征的算法，因而对于较简单的场景、较小的训练集，传统算法的优势明显。这也是为什么早在上个世纪就出现了各种神经网络，但是直到21世纪以后，基于神经网络的深度学习在人脸识别中的应用才逐渐进入主流——巨型人脸数据集与深层神经网络的搭建与计算机算力的进步。
另一个发现是，在训练轮次等参数确定的情况下，相比于传统方法，卷积神经网络对不同数据集的适应性较强，或者说稳定性较强——实验中，在不同的人脸数据集下，卷积神经网络的准确率稳定在0.8~0.9之间，而传统方法的准确率的方差较大。这其实与两者的原理直接相关，人工设计在无约束环境中对不同变化情况稳健的特征是很困难的，这使得过去的研究者侧重研究针对每种变化类型的专用方法，比如能应对不同年龄的方法、能应对不同姿势的方法、能应对不同光照条件的方法等；但是深度学习则不然，它们可用非常大型的数据集进行训练，从而学到人脸图像中稳健的特征，能够应对在训练过程中使用的人脸图像所呈现出的真实世界变化情况。

附：关键代码

1. 图像加载与图像矩阵列表建立（PCA、LDA）

def load_img(file_name):
    """
    载入图像，统一尺寸，灰度化处理，直方图均衡化
    :param file_name: 图像文件名
    :return: 图像矩阵
    """
    t_img_mat = cv2.imread(file_name)  # 载入图像
    t_img_mat = cv2.resize(t_img_mat, IMG_SIZE)  # 统一尺寸
    t_img_mat = cv2.cvtColor(t_img_mat, cv2.COLOR_RGB2GRAY)  # 转化为灰度图
    img_mat = cv2.equalizeHist(t_img_mat)  # 直方图均衡
    return img_mat


def create_img_mat(dir_name, algorithm=0):
    """
    生成图像样本矩阵，组织形式为行为属性，列为样本
    :param dir_name: 包含训练数据集的图像文件夹路径
    :param algorithm: 识别算法，0-EigenFace，1-Fisher，2-LBP
    :return: 样本矩阵，标签矩阵
    """
    data_mat = np.zeros((IMG_SIZE[0] * IMG_SIZE[1], 1))
    label = []
    data_list = []
    for parent, dir_names, file_names in os.walk(dir_name):
        for t_dir_name in dir_names:
            for sub_parent, sub_dir_name, sub_file_names in os.walk(parent + '/' + t_dir_name):
                for t_index, t_file_name in enumerate(sub_file_names):
                    if not t_file_name.endswith('.jpg'):
                        continue
                    if t_file_name.endswith('.10.jpg'):
                        continue
                    t_img_mat = load_img(sub_parent + '/' + t_file_name)
                    img_mat = np.reshape(t_img_mat, (-1, 1))

                    if algorithm == 0:
                        data_mat = np.column_stack((data_mat, img_mat))
                    else:
                        data_mat = img_mat if t_index == 0 else np.column_stack((data_mat, img_mat))

                    label.append(sub_parent + '/' + t_file_name)
            data_list.append(data_mat[:, 1:] if algorithm == 0 else data_mat)
    return data_mat[:, 1:], label, data_list

2. 图像列表建立（LBP）

class AlgorithmLbp(object):
    def __init__(self):
        self.table = {}
        self.ImgSize = IMG_SIZE
        self.BlockNum = DIM
        self.count = 0

    def load_img_list(self, dir_name):
        """
        加载图像矩阵列表
        :param dir_name:文件夹路径
        :return: 包含最原始的图像矩阵的列表和标签矩阵
        """
        img_list = []
        label = []
        for parent, dir_names, file_names in os.walk(dir_name):
            for t_dir_name in dir_names:
                for sub_parent, sub_dir_name, sub_filenames in os.walk(parent + '/' + t_dir_name):
                    for file_name in sub_filenames:
                        img_list.append(load_img(sub_parent + '/' + file_name))  
                        label.append(sub_parent + '/' + file_name)
        return img_list, label

3. 直方图建立（LBP）

class AlgorithmLbp(object):
    def get_hop_counter(self, num):
        """
        计算二进制序列是否只变化两次
        :param num: 数字
        :return: 01变化次数
        """
        bin_num = bin(num)
        bin_str = str(bin_num)[2:]
        n = len(bin_str)
        if n < 8:
            bin_str = "0" * (8 - n) + bin_str
        n = len(bin_str)
        counter = 0
        for i in range(n):
            if i != n - 1:
                if bin_str[i + 1] != bin_str[i]:
                    counter += 1
            else:
                if bin_str[0] != bin_str[i]:
                    counter += 1
        return counter

    def get_table(self):
        """
        生成均匀对应字典
        :return: 均匀LBP特征对应字典
        """
        counter = 1
        for i in range(256):
            if self.get_hop_counter(i) <= 2:
                self.table[i] = counter
                counter += 1
            else:
                self.table[i] = 0
        return self.table

    def get_lbp_feature(self, img_mat):
        """
        计算LBP特征
        :param img_mat:图像矩阵
        :return: LBP特征图
        """
        m = img_mat.shape[0]
        n = img_mat.shape[1]
        neighbor = [0] * 8
        feature_map = np.mat(np.zeros((m, n)))
        t_map = np.mat(np.zeros((m, n)))
        for y in range(1, m - 1):
            for x in range(1, n - 1):
                neighbor[0] = img_mat[y - 1, x - 1]
                neighbor[1] = img_mat[y - 1, x]
                neighbor[2] = img_mat[y - 1, x + 1]
                neighbor[3] = img_mat[y, x + 1]
                neighbor[4] = img_mat[y + 1, x + 1]
                neighbor[5] = img_mat[y + 1, x]
                neighbor[6] = img_mat[y + 1, x - 1]
                neighbor[7] = img_mat[y, x - 1]
                center = img_mat[y, x]
                temp = 0
                for k in range(8):
                    temp += (neighbor[k] >= center) * (1 << k)
                feature_map[y, x] = self.table[temp]
                t_map[y, x] = temp
        feature_map = feature_map.astype('uint8')  
        t_map = t_map.astype('uint8')
        self.count += 1
        return feature_map

    def get_hist(self, roi):
        """
        计算直方图
        :param roi:图像区域
        :return: 直方图矩阵
        """
        hist = cv2.calcHist([roi], [0], None, [59], [0, 256])  
        return hist

4. 测试图像距离计算（PCA、LDA）

def method_compare(mat_list, test_img_vec, algorithm=0):
    """
    比较函数，这里只是用了最简单的欧氏距离比较，还可以使用KNN等方法，如需修改修改此处即可
    :param mat_list: 样本向量集
    :param test_img_vec: 测试图像向量
    :param algorithm: 识别算法，0-EigenFace，1-Fisher，2-LBP
    :return: 与测试图片最相近的图像文件名的index
    """
    dis_list = []
    if algorithm == 0:
        for sample_vec in mat_list.T:
            dis_list.append(np.linalg.norm(test_img_vec - sample_vec))

    elif algorithm == 1:
        # print('mat_list.len=', len(mat_list))
        for trans_mat in mat_list:
            for sample_vec in trans_mat.T:
                dis_list.append(np.linalg.norm(test_img_vec - sample_vec))
    index = np.argsort(dis_list)[0]
    return index

5. 测试图像距离计算（LBP）

class AlgorithmLbp(object):
    def compare(self, sampleImg, test_img):
        """
        比较函数，这里使用的是欧氏距离排序，也可以使用KNN，在此处更改
        :param sampleImg: 样本图像矩阵
        :param test_img: 测试图像矩阵
        :return: k2值
        """
        testFeatureMap = self.get_lbp_feature(test_img)
        sampleFeatureMap = self.get_lbp_feature(sampleImg)
        # 计算步长，分割整个图像为小块
        ystep = int(self.ImgSize[0] / self.BlockNum)
        xstep = int(self.ImgSize[1] / self.BlockNum)

        k2 = 0
        for y in range(0, self.ImgSize[0], ystep):
            for x in range(0, self.ImgSize[1], xstep):
                testroi = testFeatureMap[y:y + ystep, x:x + xstep]
                sampleroi = sampleFeatureMap[y:y + ystep, x:x + xstep]
                testHist = self.get_hist(testroi)
                sampleHist = self.get_hist(sampleroi)
                k2 += np.sum((sampleHist - testHist) ** 2) / np.sum((sampleHist + testHist))
        return k2

6. 学累了，听首歌放松一下吧！

posted @ 2020-05-31 20:09 FUJI_W 阅读(17404) 评论(4) 编辑收藏举报

刷新页面返回顶部

FUJI_W

图像处理 人脸识别的三种经典算法与简单的CNN 【附Python实现】

一点说明

1. 完成情况

2. 项目结构

思路分析

0. 人脸识别 综述

1. 传统算法——主成分分析（PCA）与 线性判别分析（LDA）

1）算法框架

2）PCA 原理

I. 为什么要降维？

II. PCA降维的原理是什么？

III. 如何使用PCA进行降维？

IV. PCA的缺点与不足

V. PCA 的 python 实现

3）LDA 原理

I. LDA的原理是什么？

II. LDA 与 PCA 的比较

III. LDA 的 python 实现

3. 传统算法——局部二进制模式直方图（LBPH）

I. LBP 的原理是什么？

III. LBPH 的算法流程

III. LBP 的特点？

IV. LBPH 的 python 实现

4. 神经网络——卷积神经网络（CNN）

I. 深度学习的几个经典的案例

II. 深度学习的算法流程

III. Python实现

结果分析

0. 数据集说明

I. 基本信息（数据集地址）

II. 数据集展示

1. 主成分分析（PCA）

I. PCA算法中的 “平均脸” 与 “特征脸”

II. 准确率与消耗时间

III. PCA 结果分析

2. 线性判别分析（LDA）

I. LDA中的平均脸

II. 准确率与消耗时间

III. LDA 结果分析

3. 局部二进制模式直方图（LBPH）

I. LBPH 中间图像

II. 准确率与消耗时间

III. 结果分析

IV. 三种经典算法的准确率对比

V. 三种经典算法的速度对比

4. 卷积神经网络（CNN，分类模型）

I. 准确率与损失函数收敛情况

II. 分析（与经典算法的对比）

附：关键代码

1. 图像加载与图像矩阵列表建立（PCA、LDA）

2. 图像列表建立（LBP）

3. 直方图建立（LBP）

4. 测试图像距离计算（PCA、LDA）

5. 测试图像距离计算（LBP）

6. 学累了，听首歌放松一下吧！

公告

图像处理人脸识别的三种经典算法与简单的CNN 【附Python实现】

0. 人脸识别综述

1. 传统算法——主成分分析（PCA）与线性判别分析（LDA）